Block 3 Models

A project about present and future value

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

In this project, we’re going to study some statistics of life and death. Specifically, we’re going to look at “period life tables” assembled and published by the US Social Security Administration.

The M2014F data frame is basic data from 2014 on age-specific mortality, that is, the risk of a person of any given age having died in 2014. The table below is for females; there is a similar table for males on the Social Security website.

Scroll through the data until you are comfortable with the format. The variables year and age are self explanatory. pmort is the probability of a person of the given age having died in the next year. nliving and died are not counts from the population but a construction of a theoretical cohort of 100,000 newborn people whose lives are such as to follow, at any age, the mortality at that age. Thus, given the age-specific mortality in 2014, of the theoretical 100,000 newborns, 99,342 would still be alive at the end of age 10. died is the number from the theoretical cohort who would have died during the given the value number who are still alive at any age. While not exact basically nliving - died within an age will output nliving for the following age.

Essay 1: For the following essay question ensure that your answer is in the form of complete sentences and utilizes proper grammar.Explain why in the first row nliving + ndead does not add up to 100,000. Additionally, explain why nliving in row 4 is equal to 99,412 (In other words, how was the number calculated).

question id: retirement-essay-1

According to the table, which age is the safest, that is, has the least risk of dying? Hint: it may be easiest to use the headings to sort

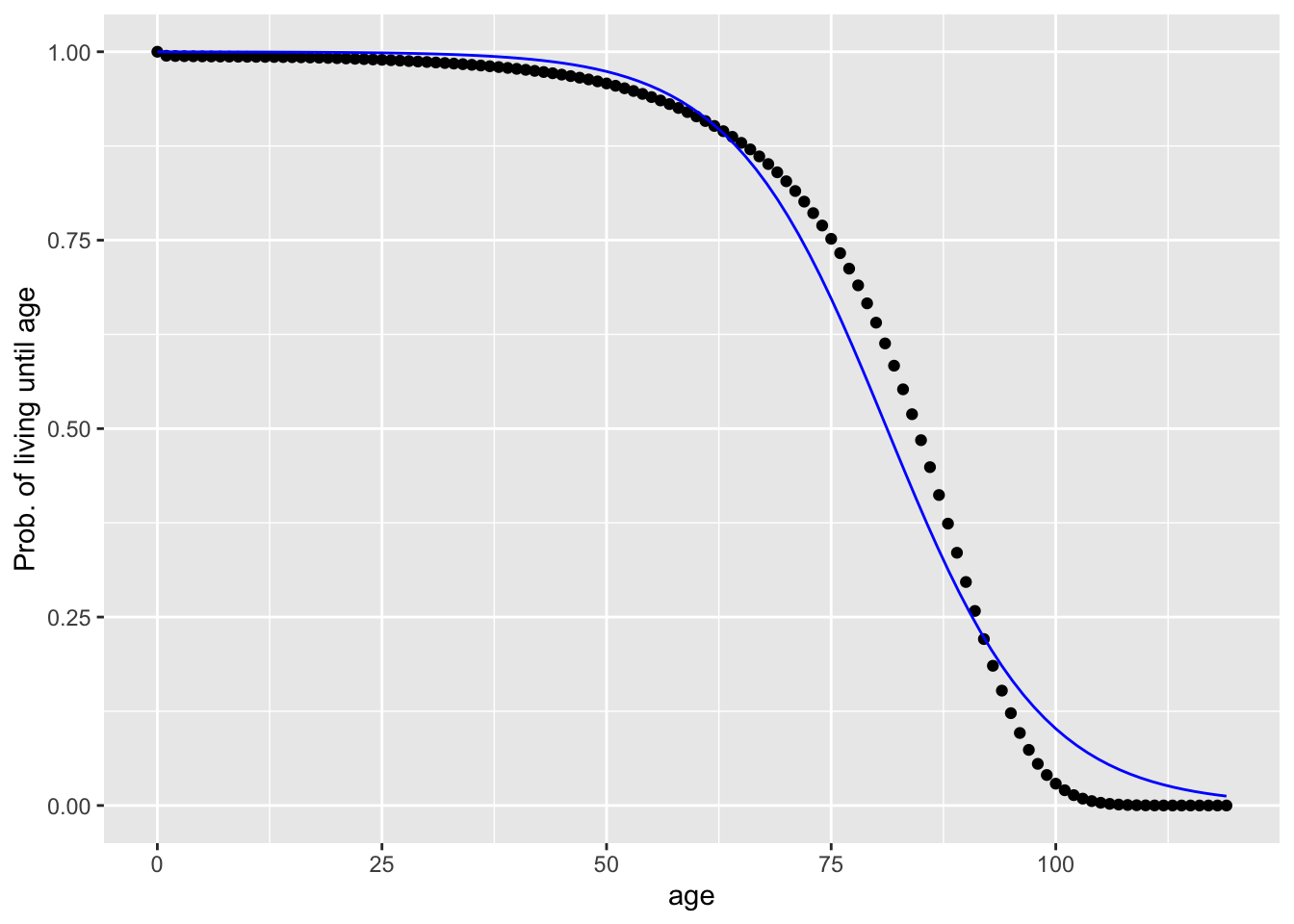
Active R chunk 1 makes a plot of the mortality rate as a function of age. By default, the plot is being made with semi-log axes, but you can change the code to make the plot on linear axes or on log-log axes.

Active R chunk 1

The pattern of mortality vs age has a complex shape that becomes simpler if we split the domain into a handful of epochs. Use the various kinds of axes scaling to answer each of these questions.

For children age 1 to about 10 years, which of these function forms best matches the data? Hint: you can scale the x-axis using the gf_refine function by adding a similiar function as an argument.

Is the mortality rate for babies in their first year in line with the pattern seen for other pre-adolescents?

yes no

question id: retirement-3

For adults age 25 to about 90 years, which of these function forms best matches the data (mortality v. age)?

We’re going to work with people who have an interest in eventual retirement, either saving for it or drawing from their savings. We could make a cubic spline function that fits the data, but the data are already very smooth and even a straight-line interpolant would be adequate. Instead, we will employ an easy to use method that models log mortality versus age using a small set of basis functions, shown in the following graph:

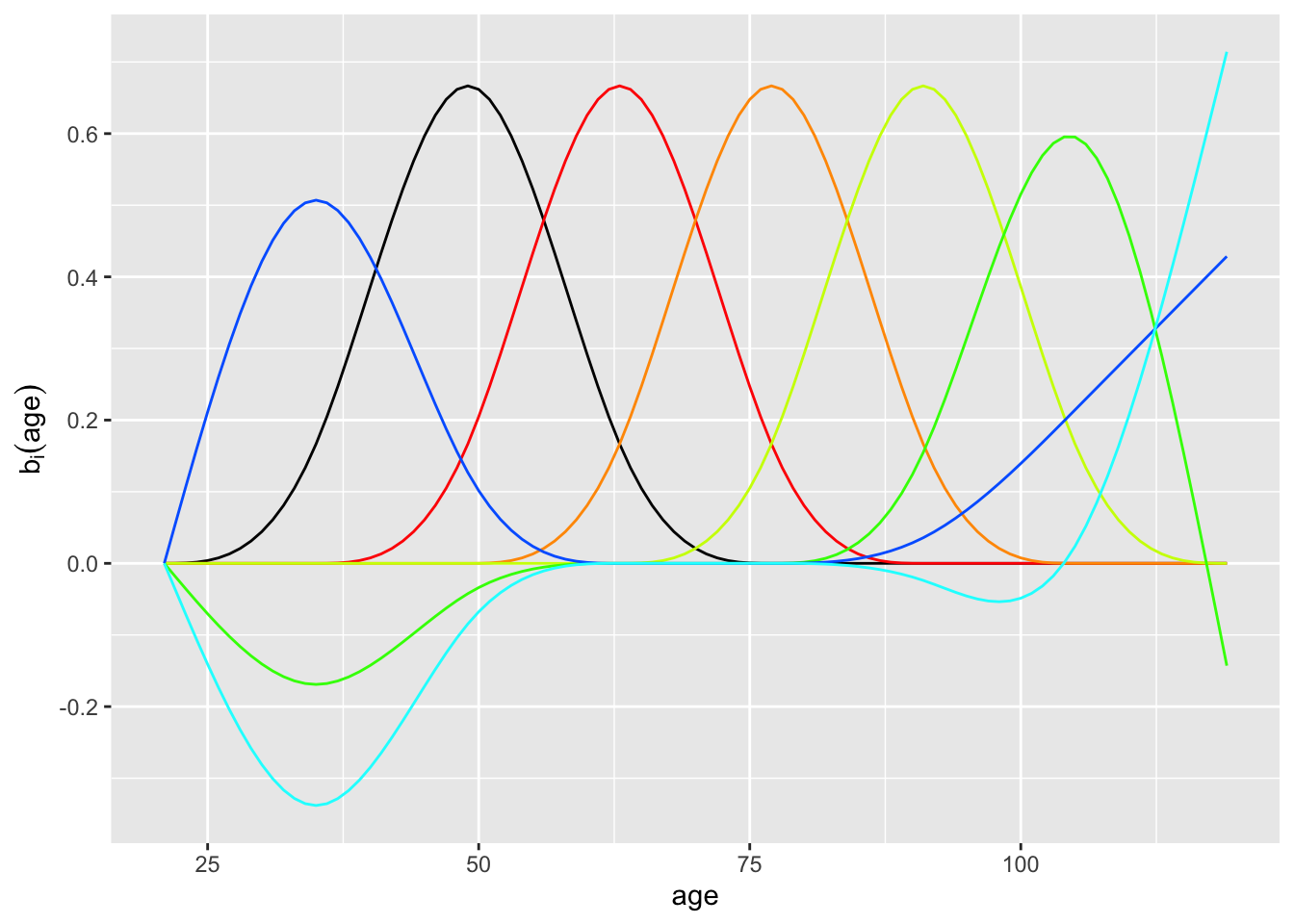
There are seven basis functions used for the model of mortality versus age. They fall into two groups: (1) the “purely local” hump functions and (2) the functions that have something to say at the beginning and end of the domain. Which of the following colors or groups of colors are a member of group (2)?

Expected Social Security

Simplifying a little, Social Security works like this: All workers have a payroll tax that is considered their “contribution” to the Social Security fund. At retirement (currently age 67) and until death, the worker receives a monthly stipend off approximately $2000.

Our goal is to calculate the net present value of this stipend stream from the point of view of a 67-year old. Here are the components of the calculation:

A stipend at the rate of $24,000 per year paid over multiple years.
Discounting each stipend payment at an annual (continuously compounded) interest rate of 2%.
Further discounting the stipend payment by the probability that a person will be alive at any given number of years into retirement.
Accumulating all the (discounted) stipends.

(1) and (2) are easy. At age $y$, the stipend stream is worth \[ s(y) = 24000 \times e^{0.02(y-67)}\]

(3) requires a bit more work. We’ll focus on the number of people (in the hypothetical population) still living. Here’s the data, along with a not-very-good function approximating the data. The method used to construct the model, logistic regression, is not one you have seen before. We’ll use it here, treating it as a black box. You don’t need to worry about how it works other than to know it constructs an appropriately shaped function from data.

# Construct a model of the probability
# by a special technique called "logistic regression"
prob_living <- makeFun(
  glm(nliving/100000 ~ age, data = M2014F, 
      family = binomial)
)

Warning in eval(family$initialize): non-integer #successes in a binomial glm!

gf_point(nliving/100000 ~ age, data = M2014F) %>%
  slice_plot(prob_living(age) ~ age, color="blue") %>%
  gf_labs(y="Prob. of living until age")

There are seven basis functions used for the model of mortality versus age. They fall into two groups: (1) the “purely local” hump functions and (2) the functions that have something to say at the beginning and end of the domain. Which of the following colors or groups of colors are a member of group (2)?

The function fitted to the data is not very good. You’re going to make it better using the same technique we used with the mortality vs age data. Specifically, instead of the tilde expression nliving/100000 ~ age, you will use nliving/100000 ~ ns(age,??), where the ?? must be replaced with a small integer saying how many basis functions to use. Start with 2 and increase gradually until the graph of the function goes right through the data points. Only change the first tilde function inside the makeFun function not both.

How many basis functions is enough to get the fitted function to go right through the data? Choose the smallest number. When you get the correct answer make sure you rerun your sandbox above with the correct answer.

Important technical note: We are providing you with our own prob_living() function in order to play well with the other software in this document. It’s the same function mathematically as the one you created in the sandbox (using the correct answer to the previous question).

The function prob_living() is our model of someone living to a given age, but who is that person. The way prob_living() is written, that person is someone just born. But, insofar as we are interested in the present value of Social Security payments made to a person who starts at age 67, we have to take it for granted that this person is still alive. So the probablity that a (relevant) person is alive at 67 is 100%. We need to modify prob_living() to take this into account. This is easy; just divide prob_living() by its numerical value at age 67. That will make the overall output 100% at age 67.

What is the number you need to divide into the output of prob_living() in order to get an overall output of 100% at age 67? In other words, what is the output of prob_living() at an input age of 67?

Now we can put together all the components we need for component (3) as described above: the present value of the instantaneous average Social Security payment to a person of age $y$.

24000 * exp(0.02*(y-67)) * prob_living(y)/0.8574

Using R, implement this function, and accumulate it from age 67 to age 100. Hint: When you see the word accumulate regarding a continuous function, you should immediately think integrate.

According to the model, what is roughly the net present value (at a 2% discount rate) of a $2000/month Social Security income stream for a 67-year old just starting to collect?

Before you do a complicated calculation, you should have in mind what the answer will be so that you can make sure the result of your calculation is reasonable. You may well ask, “How am I supposed to know the result before I do the calculation itself?” The answer: you should have a simple technique to get a ballpark estimate for the answer.

In this situation, you might do the following:

In your simple approximation, ignore the discounting. At 2% per year, it takes about 36 years for the 2% discount to cut the value by half, and not so many people live to be 67 + 36.
Instead of using a probability of being alive at any age, just make a good estimate of how long a typical 67-year old lives. You can make such an estimate simply from the graph of prob_living() shown above. Let’s say the estimate is 18 years.
Multiply the yearly payment by the number of years of life, so $24,000 $\times 18 =$ $432,000.

Essay 2: For the following essay question ensure that your answer is in the form of complete sentences and utilizes proper grammar.A classmate runs their model and finds the answer to be $1,121,751. Your classmate did a reasonable calculation, but has failed to account for something. What did they forget to account for? Hint: use the sandbox above removing aspects of the equation to find what was neglected. Your answer should explain in everyday words what is missing (not the mathematical portion of the equation that is missing).

question id: retirement-essay-2

Life expectancy

You now have most of the apparatus to calculate one of the most commonly used indices of public health and yet one highly mis-understood by most decision makers: Life expectancy.

First, you need the model of the probability of dying at any exact given age. Then, calculate the **expectation value* of age according to this probability model.

We already have a probability of survival as a function of age: prob_living(). At first it might seem to you that the probability of dying at age $y$ is 1 - prob_living(y) (in otherwords the opposite of probability of dying at any exact age in the opposite of probability of survival), but that’s not true. Why not? Because 1 - prob_living(y) is a probability of dying at age $y$ or before. That is, it is the accumulated probability across all people.

We need to “de-accumulate” the probability, to get to the change in probability from one year to the next. Let’s replace the word “accumulation” with its calculus synonym: anti-derivative. We we need to “de-anti-derivative” the 1 - prob_living(y) function. That is, it’s the derivative of 1 - prob_living(y) that we want.

Modify the R statements to compute the expectation value of age. Recall that an expectation value of a quantity $y$ is $\int y\, p(y) dy$ over the relevant domain.

According to our model prob_living(), what’s the expectation value of age (that is, “life expectancy” for females born in 2014)?

Possibly you didn’t follow the (brief) argument about why to use the derivative of 1 - prob_living(y) instead of just 1 - prob_living(y) itself. So let’s try it out and see what we get:

Does that seem reasonable based upon your experience? Explain why or why not.

question id: retirement-essay-reasonable

Misunderstanding life expectancy

What’s there to mis-understand about life expectancy? I’m not referring to the calculation itself, which puts together some challenging concepts like differentiation, integration, and function fitting.

The fundamental mistake is to use the short form of the name, “life expectancy” rather than the full name, “life expectancy at age ___.” The number you hear about is “life expectancy at birth.”

People use life expectancy at birth to make decisions about things for which it is misleading. For instance, in public debates about health care, you will often hear that other rich nations have longer life expectancy than the US even though they spend half as much money per capita on health care. But the low US life expectancy is shaped largely by some features not so relevant to health care: the relatively high infant mortality in the US (which has it’s own set of factors), the high teenager mortality (which is not as clear when only looking at the data for females), gun deaths, etc.

Since the large majority of health-care spending is for seniors, we should look at the outcome for seniors. For instance, we might want to look at life expectancy at age 67. Let’s calculate that. Note that the calculation is the same as the above, but prob_living(y) has been adjusted so that it applies to people who reach age 67.

Essay 3: For the follwing essay question ensure that your answer is in the form of complete sentences and utilizes proper grammar. The immediately above calculation found life expectancy to be 85.8346. This number is larger than the life expectancy that was calculated in the previous section (81.04189). Why is that? Be sure to explain what both numbers are in your response.”

question id: retirement-essay-3

No answers yet collected