Sigmoid intro

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1  

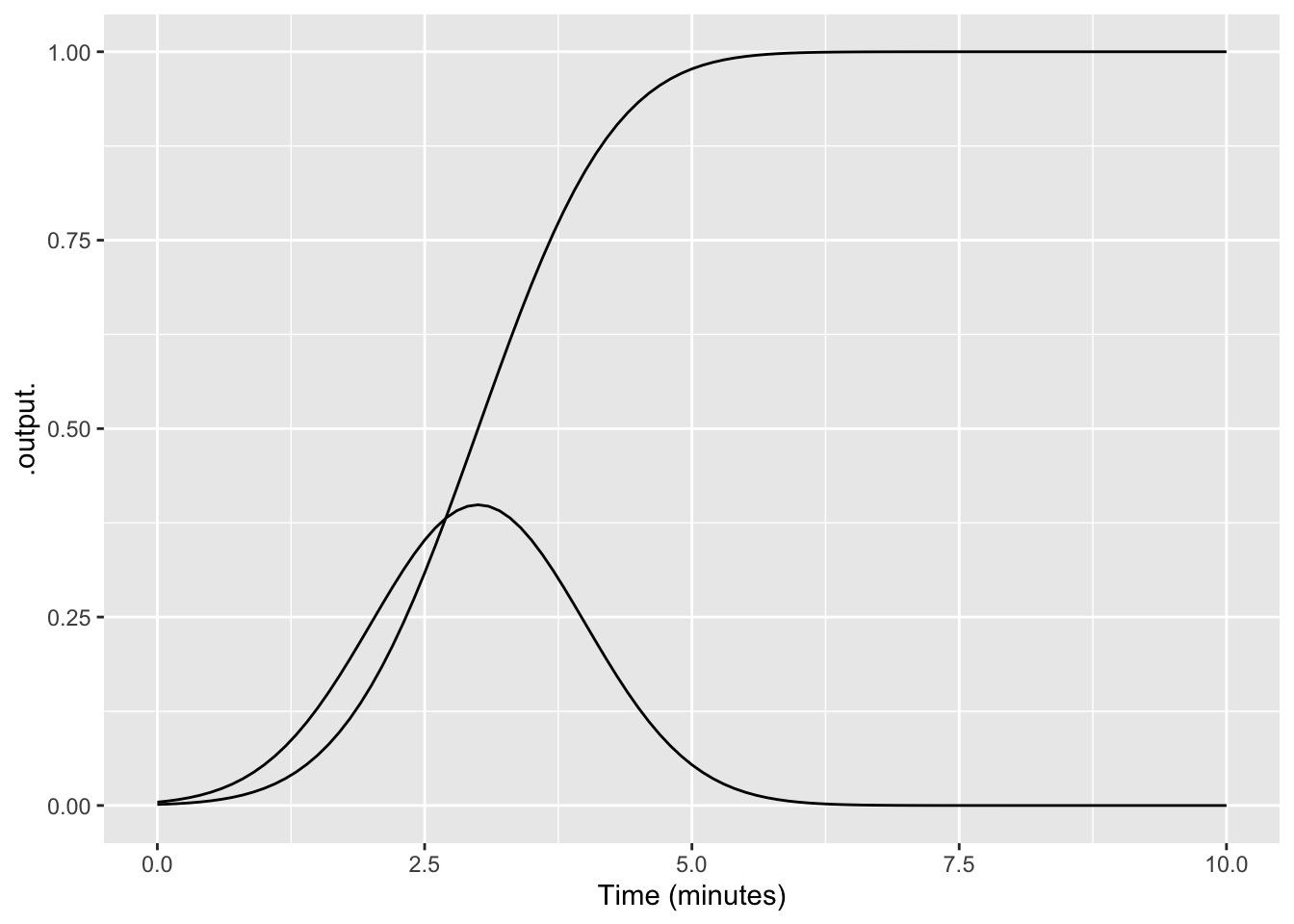
Figure 1: A gaussian function and the sigmoid function that corresponds to it.

Which of these stories is consistent with the relationship between a gaussian and its corresponding sigmoid shown in Figure fig-gaussian-sigmoid?

The gaussian is the amount of water in a bathtub while the sigmoid is the time you spend in the bath.

The gaussian is the amount of water in the bathtub while the sigmoid is the rate at which water flows from the tap.

The gaussian is the rate at which water flows from the tap and the sigmoid is the amount of water in the bathtub.

The gaussian indicates the amount the drain is open and the sigmoid is the amount of water in the bathtub.

question id: dd-08-1

Exercise 2 Gaussian functions and sigmoid functions come in pairs. For every possible sigmoid, there is a corresponding gaussian that gives, for each value of the input, the slope of the sigmoid.

Each of the following graphs shows a sigmoid and a gaussian function. The two might or might not correspond to one another. That is, the output of the gaussian might be the slope of the sigmoid, or the gaussian might correspond to some other sigmoid. Remember, you’re comparing the output of the gaussian to the slope of the sigmoid.

For each graph, say whether the gaussian and the sigmoid correspond to one another. Is so, choose correspond. If not, choose one of these reasons why not:

  • center: The peak of the gaussian does not occur at the same value of \(x\) at which the sigmoid is steepest.
  • amplitude: The numerical value of the output of the gaussian function is, for all \(x\), much larger than the numerical value of the slope of the sigmoid.

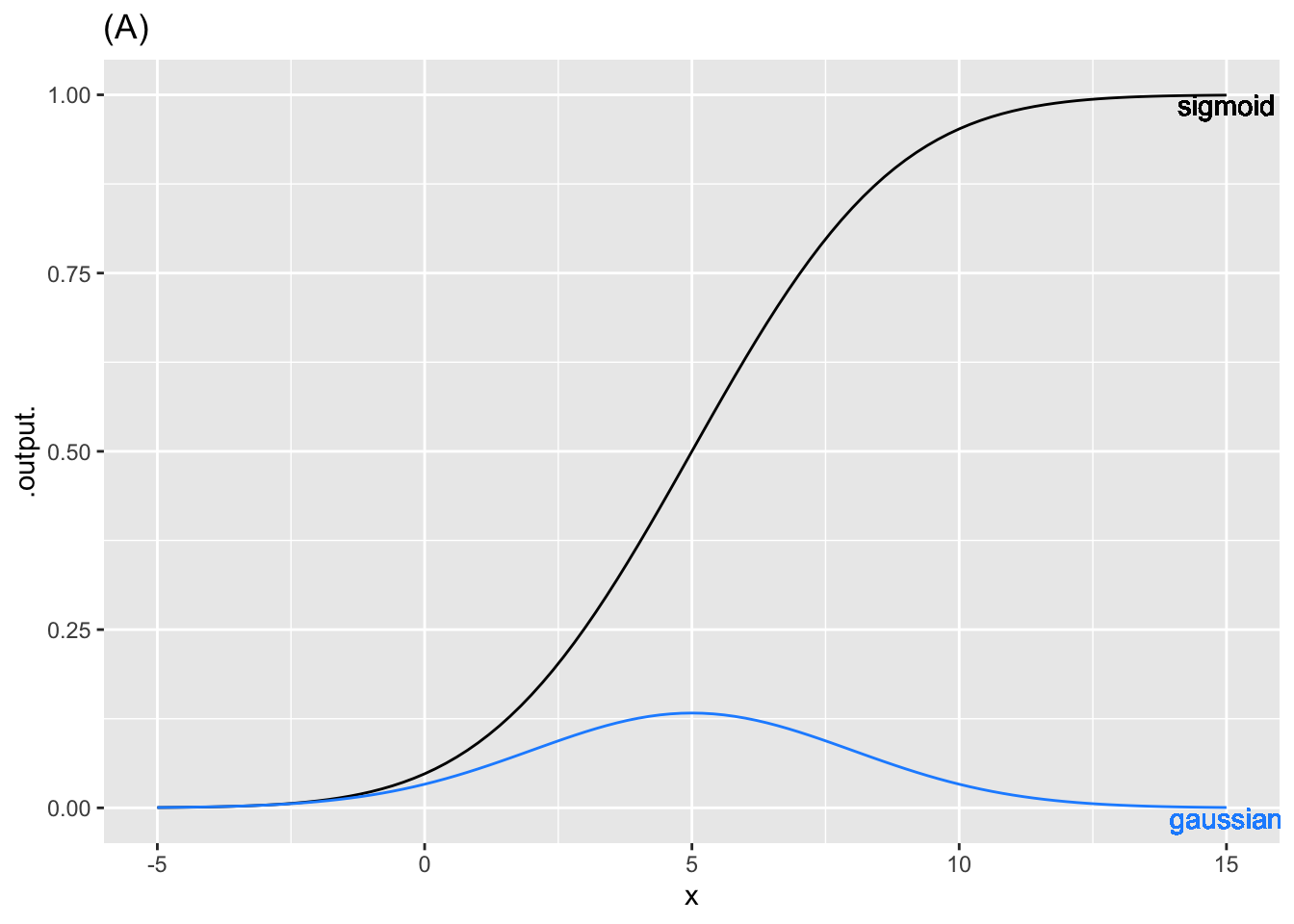
  1. Graph (A)

correspond

center

amplitude

question id: sigmoid-intro-1

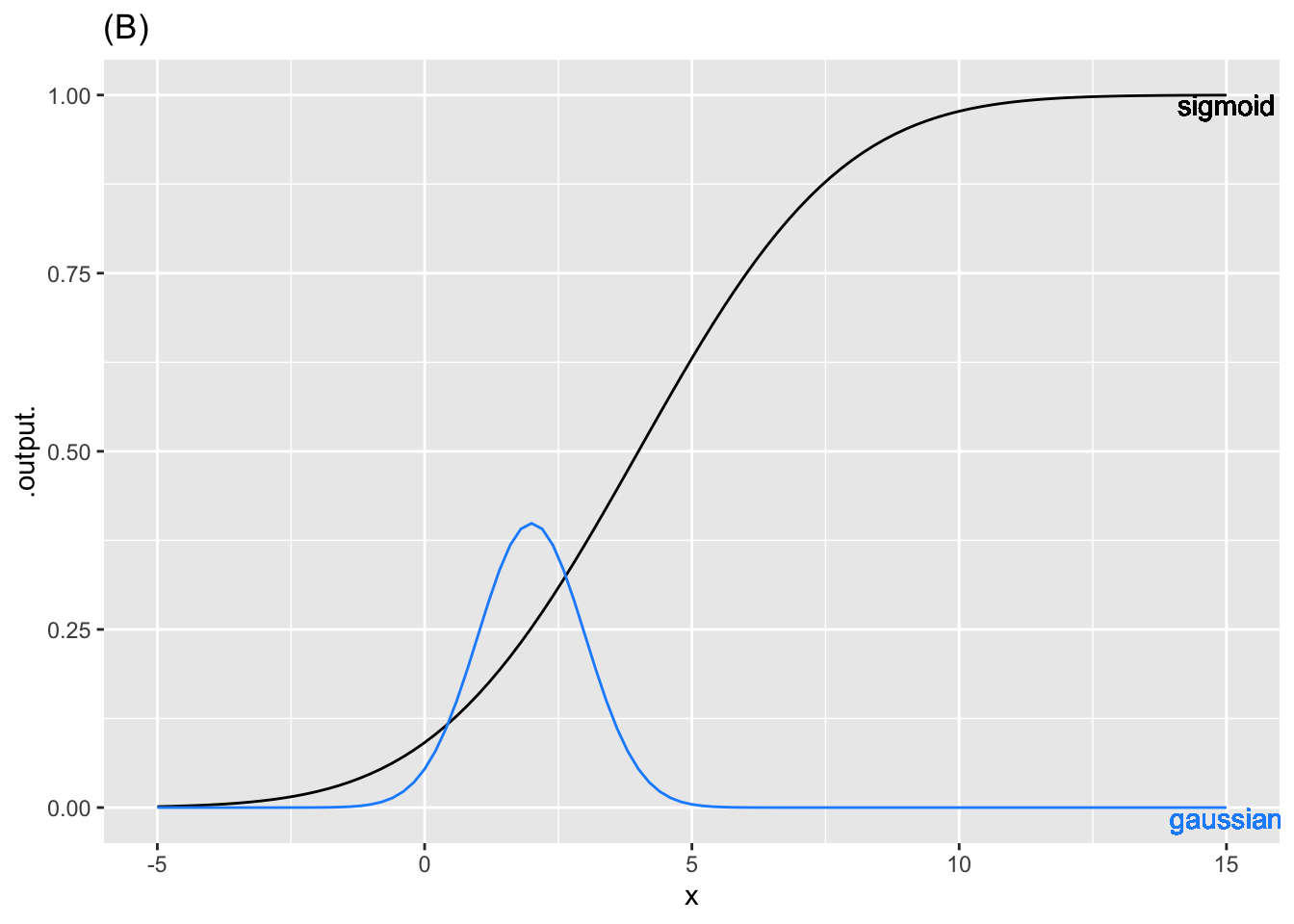
  1. Graph (B)

correspond

center

The numerical value of the output of the gaussian function is much larger than the numerical value of the slope of the sigmoid.

question id: sigmoid-intro-2

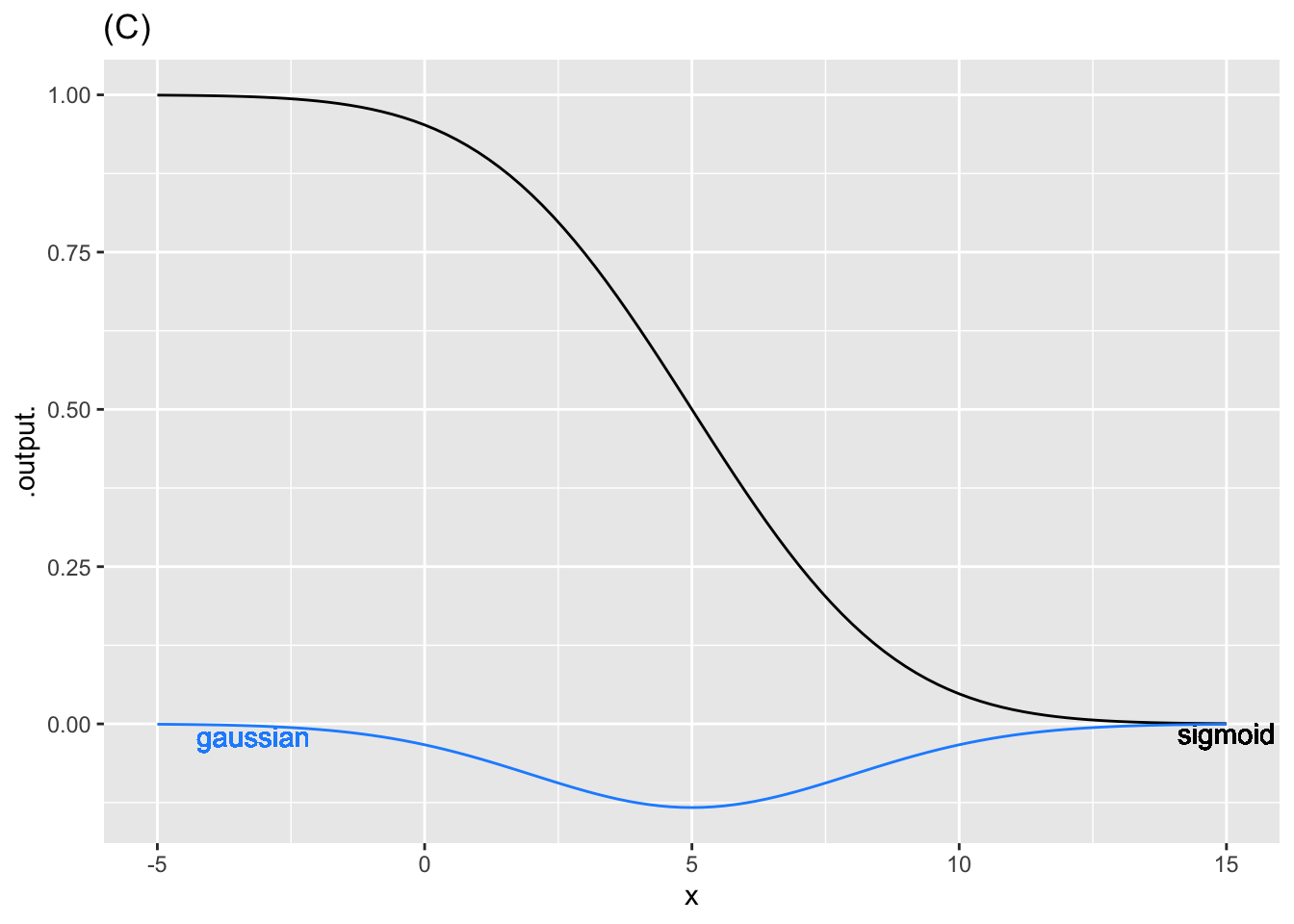
  1. Graph (C)
correspond       center       amplitude      

question id: sigmoid-intro-3

Exercise 3  

Figure 2: Several gaussian functions along with a single sigmoid function.
  1. Which of these statements is true?

The gaussian is the derivative of its corresponding sigmoid.

The sigmoid is the derivative of its corresponding gaussian.

Gaussians and sigmoids are unrelated.

question id: exr-boy-hide-gloves-1

  1. Which gaussian in Figure fig-gaussian-sigmoid corresponds to the sigmoid?
A       B       C       D      

question id: boy-hide-gloves-2

Exercise 4 Here are graphs of various functions. The right column shows functions named \(f_1()\), \(f_2()\), and so on. The left column shows functions \(A()\), \(B()\), \(C()\), and so on. Most of the functions on the right are the derivative of some function on the left, and most of the functions on the left have their corresponding derivative on the right. Your task: Match the function on the left to its derivative on the right.

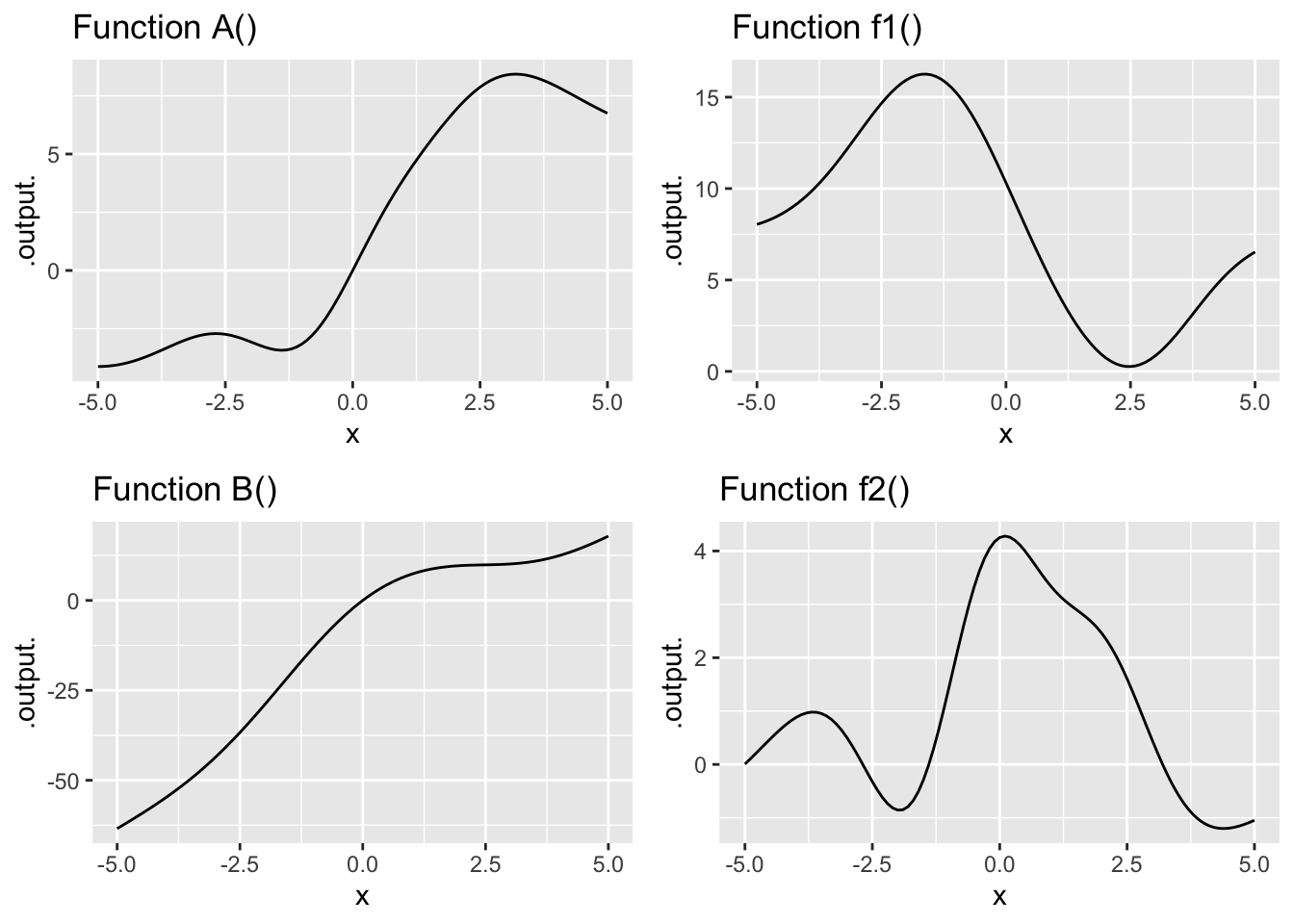
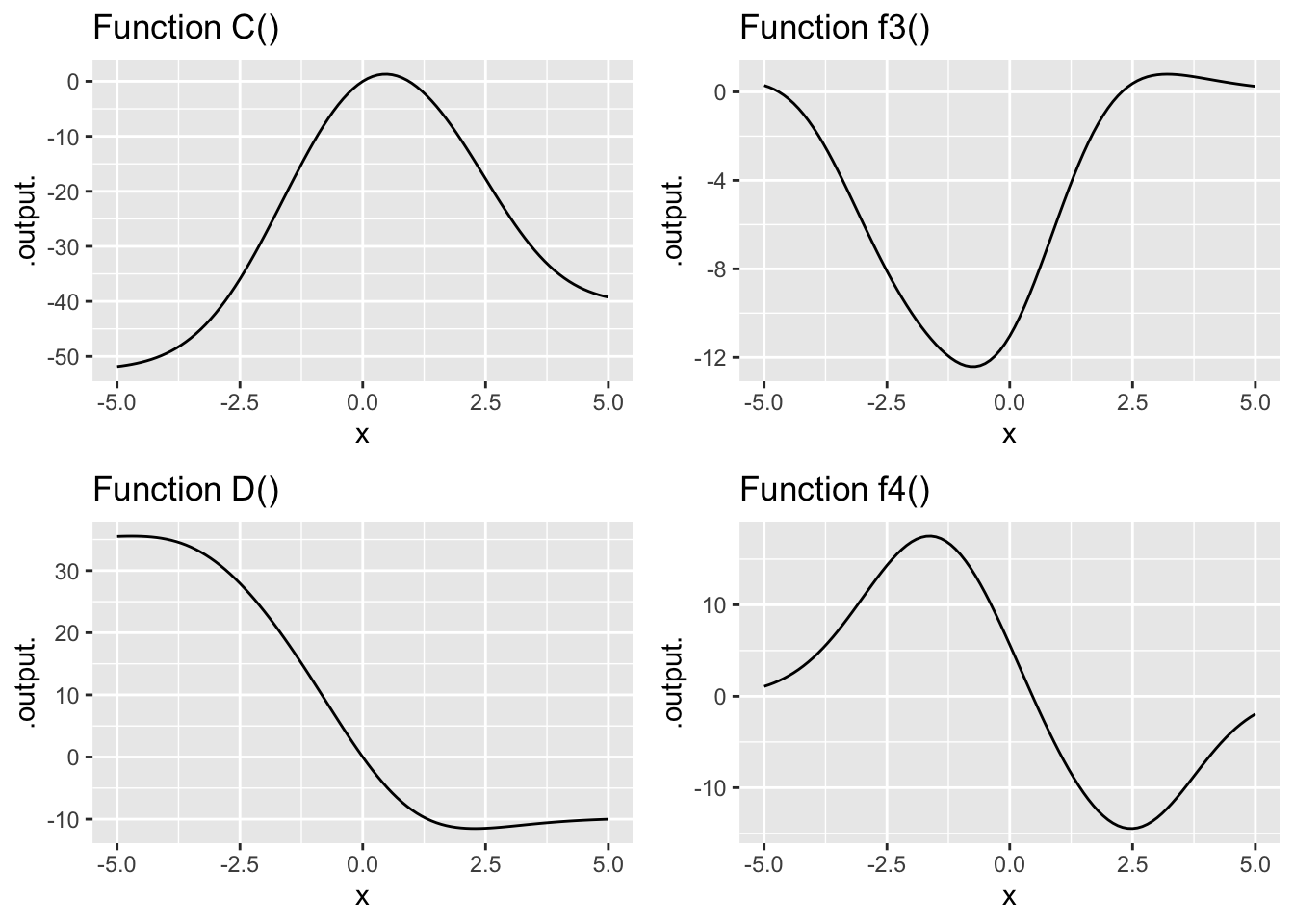
  1. The derivative of Function A() is which of the following:
f1()       f2()       f3()       f4()       not shown      

question id: robin-row-boat-1

  1. The derivative of Function B() is which of the following:
f1()       f2()       f3()       f4()       not shown      

question id: robin-row-boat-2

  1. The derivative of Function C() is which of the following:
f1()       f2()       f3()       f4()       not shown      

question id: robin-row-boat-3

  1. The derivative of Function D() is which of the following:
f1()       f2()       f3()       f4()       not shown      

question id: robin-row-boat-4

Activities

Exercise 5 In the following, three different functions are described. Your task is to write down the dimension of the input and of the output. Do this both for the function itself, and for the derivative of the function. For example, the dimension of the output of \(N(y)\) given below is P, for population. The input has dimension T, for time.

A. The given function is \(N(y)\), the population of the Netherlands in year \(y\).

  1. Dimension of input to \(N(y)\)?
  2. Dimension of output from \(N(y)\)?
  3. Dimension of input to \(\partial_y N(y)\)?
  4. Dimension of output from \(\partial_y N(y)\)?

B. The given function is \(p(u)\), the net profit from a manufactured good as a function of the number of units manufactured.

  1. Dimension of input to \(p(u)\)?
  2. Dimension of output from \(p(u)\)?
  3. Dimension of input to \(\partial_u p(u)\)?
  4. Dimension of output from \(\partial_u p(u)\)?

C. The given function is \(w(t)\), the amount of water in a leaky bucket at any time after the bucket was filled.

  1. Dimension of input to \(w(t)\)?
  2. Dimension of output from \(w(t)\)?
  3. Dimension of input to \(\partial_t w(t)\)?
  4. Dimension of output from \(\partial_t w(t)\)?

Exercise 6 We don’t yet have the tools needed to prove a formula for the derivative of power-law functions, but we already have some instances where we know the derivative:

  • \(\partial_x x^2 = 2 x\)
  • \(\partial_x x^1 = 1\)
  • \(\partial_x x^0 = 0\)

A rule that fits all these examples is \[\partial_x x^p = p\, x^{p-1}\ .\] For instance, when \(p=2\) the rule gives \[\partial_x x^2 = 2\, x^1 = 2 x\] since \(p-1\) will be 1$.

It is not too hard to do the algebra to find the derivative of \(x^3\). According to the proposed rule, the derivative should be \[\partial_x x^3 = 3 x^2\ .\]

Let’s check this via the general definition of the derivative: \[\partial_x x^3 = \underbrace{\lim_{h \rightarrow 0}}_\text{limit}\ \underbrace{\frac{(x+h)^3 - x^3}{h}}_\text{ratio}\] In the evanescent-h technique, we put aside the limit for a moment and work algebraically on the ratio with the assumption that \(h\neq0\).

  1. Expand out \((x+h)(x+h)(x+h) - x^3\) to get a linear combination of monomials: \(x^2\), \(x^1\), and \(x^0\).

  1. Divide the linear combination in (a) by \(h\) and simplify.

  2. Examine the expression from (b) to determine if setting \(h=0\) will result in a divide-by-zero. What did you find?

  3. If your conclusion from (c) is that divide-by-zero does not occur when \(h=0\), set \(h=0\) and simplify the expression from (b) to find \(\partial_x x^3\). Is your result consistent with the rule for the derivative of power-law functions described at the beginning of this problem.

No answers yet collected