Chap 9 Exercises

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

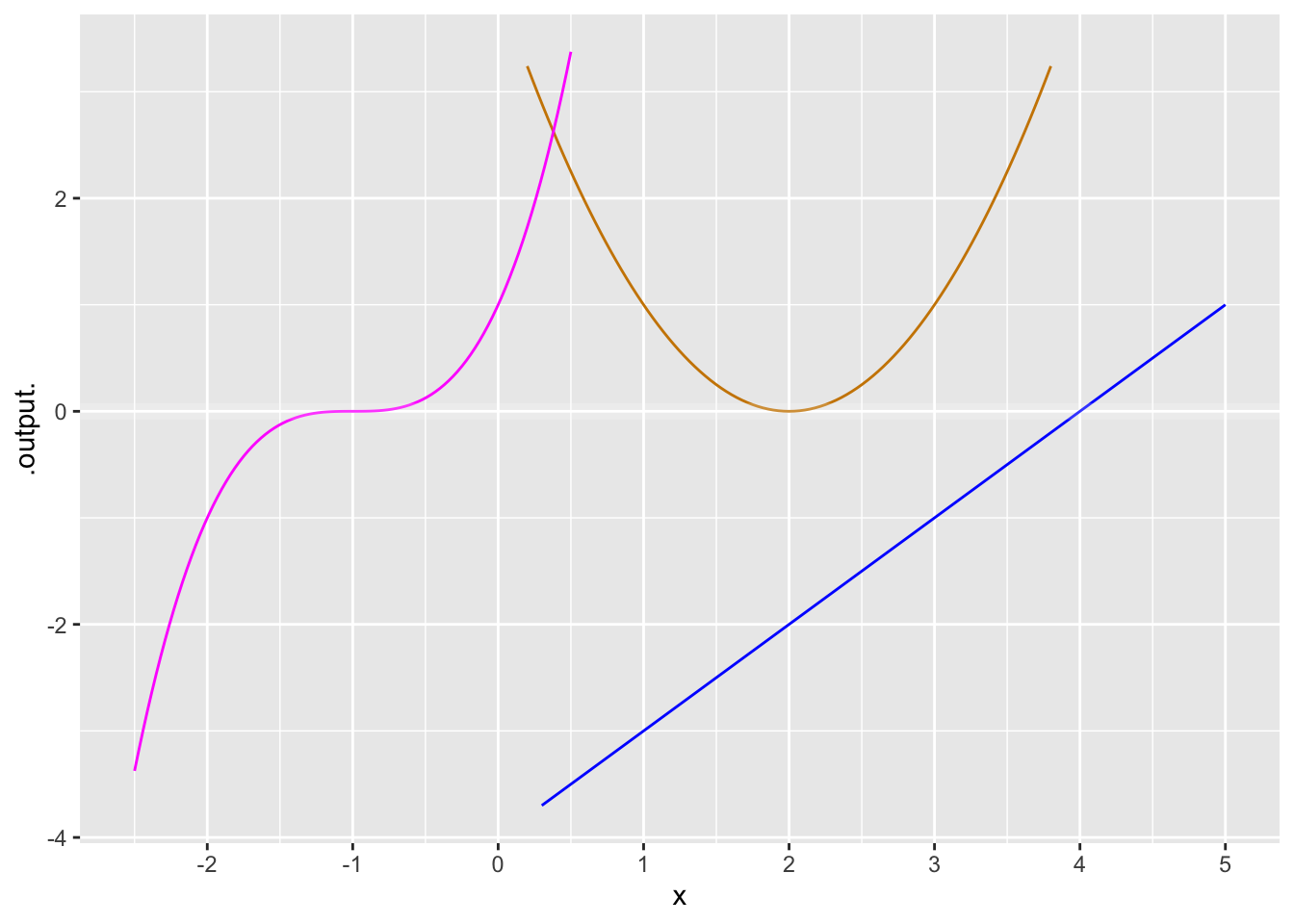
Exercise 1 Each of the three functions graphed below is a simple power-law function that can be written \(\left[\strut x-x_0\right]^n\). The three functions in Figure fig-local-shift-plot different values for \(x_0\) and for \(n\).

Figure 1

1a. For the \(\color{blue}{\text{blue}}\) function, what is \(x_0\)?

0       1       2       3       4       5 inline = TRUE      

question id: local-shift-1a

1b. For the \(\color{blue}{\text{blue}}\) function, what is the order of the polynomial?

0       1       2       3       4       5 inline = TRUE      

question id: local-shift-1b

2a. For the \(\color{orange}{\text{orange}}\) function, what is \(x_0\)?

0       1       2       3       4      

question id: local-shift-2a

2b. For the \(\color{orange}{\text{orange}}\) function, what is the order of the polynomial?

0       1       2       3       4      

question id: local-shift-2b

3a. For the \(\color{magenta}{\text{magenta}}\) function, what is \(x_0\)?

-2       -1       0       1       2      

question id: local-shift-3a

3b. For the \(\color{magenta}{\text{magenta}}\) function, what is the order of the polynomial?

0       1       2       3       4      

question id: local-shift-3b

Exercise 2 For each of the following, say whether the function \(f_?()\) is a linear combination, a multiplication, or a composition of the two simpler functions.

  1. \(f_a(t) \equiv \sin(e^x)\)
linear combination       function multiplication       function composition      

question id: dog-hunt-fabric-a

Active R chunk 1

Use Active R chunk lst-dog-hunt-fabric-plotter to plot \(f_a()\) over the domain \(0 \leq t \leq 10\) and explain the obvious ways in which \(f_a()\) differs from the pattern-book \(\sin()\).

question id: essay-dog-hunt-fabric-a

  1. \(f_b(t) \equiv e^x \sin(x)\)
linear combination       function multiplication       function composition      

question id: dog-hunt-fabric-b

Use Active R chunk lst-dog-hunt-fabric-plotter to plot \(f_b()\) over the domain \(0 \leq t \leq 10\) and explain the obvious ways in which \(f_b()\) differs from the pattern-book \(e^x\).

question id: essay-dog-hunt-fabric-b

  1. \(f_c(t) \equiv e^{\sin(t)}\)
linear combination       function multiplication       function composition      

question id: dog-hunt-fabric-c

Use Active R chunk lst-dog-hunt-fabric-plotter to plot \(f_c()\) over the domain \(0 \leq t \leq 20\) and explain the obvious ways in which \(f_c()\) differs from the pattern-book \(e^x\).

question id: essay-dog-hunt-fabric-c

Exercise 3 The function bigger() is defined piecewise in terms of two extremely simple functions. Each of the two simple functions has a contour plot with contours that are parallel. The piecewise combination of the simple functions has a more complicated contour plot, with each simple function’s parallel contours showing up in half of the domain. We will call these “pieces” of the domain.

Which of the following best describes the two pieces of the domain?

One is above and to the left of the line of identity (that is, \(y=x\)) and the other is below and to the right of that line.

One is \(x > 0\) and the other \(x \leq 0\)

One is \(x > 0\) and the other \(y \leq 0\)

question id: bigger-two

Exercise 4 The Heaviside function has two asymptotes.

Are they horizontal or vertical asymptotes?

Horizontal       Vertical       Mixed. One horizontal, one vertical.      

question id: beech-ride-table-1

  1. What are the values reached assymptotically?
1 on both sides.       0 on both sides.       0 on the left, 1 on the right.       1 on the left, 0 on the right.       None of the above.      

question id: beech-ride-table-2

Exercise 5  

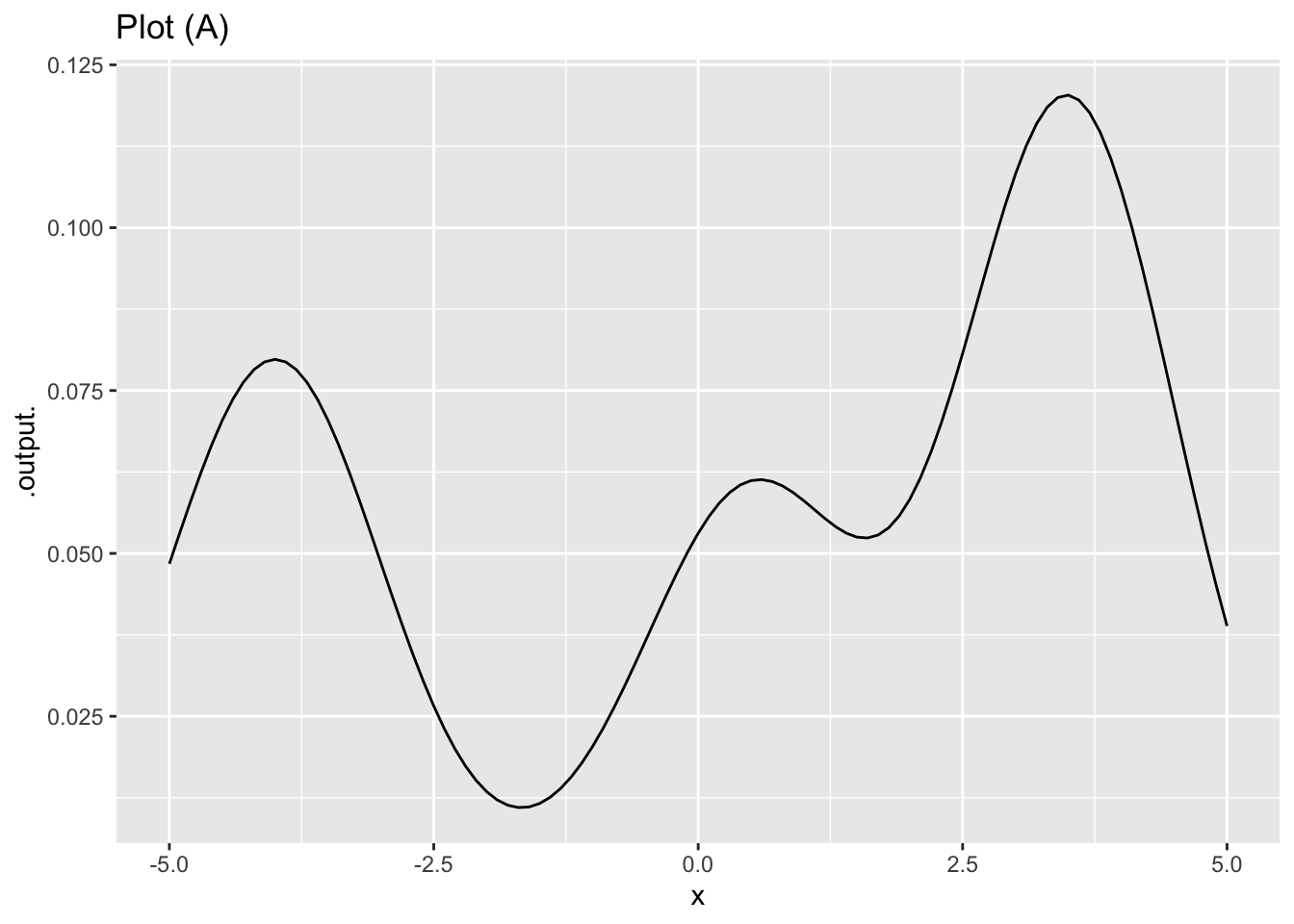
Figure 2: A linear combination of three gaussian functions.

Figure fig-road-1-1 shows a function that is a linear combination of three x-shifted gaussian functions \[a_1 \dnorm(x-3.5) + a_2 \dnorm(x-0.5) + a_3 \dnorm(x-(-4))\]

Estimate the coefficients \(a_1, a_2\), and \(a_3\) for the function drawn in Plot (A). (Be sure to get the order right!)

\(a_1 = 0.3, a_2 = 0.15, a_3=0.2\)

\(a_1 = 0.15, a_2 = 0.2, a_3=0.3\)

\(a_1 = 0.2, a_2 = 0.3, a_3=0.15\)

\(a_1 = 0.15, a_2 = 0.3, a_3=0.2\)

question id: b-road-1-1

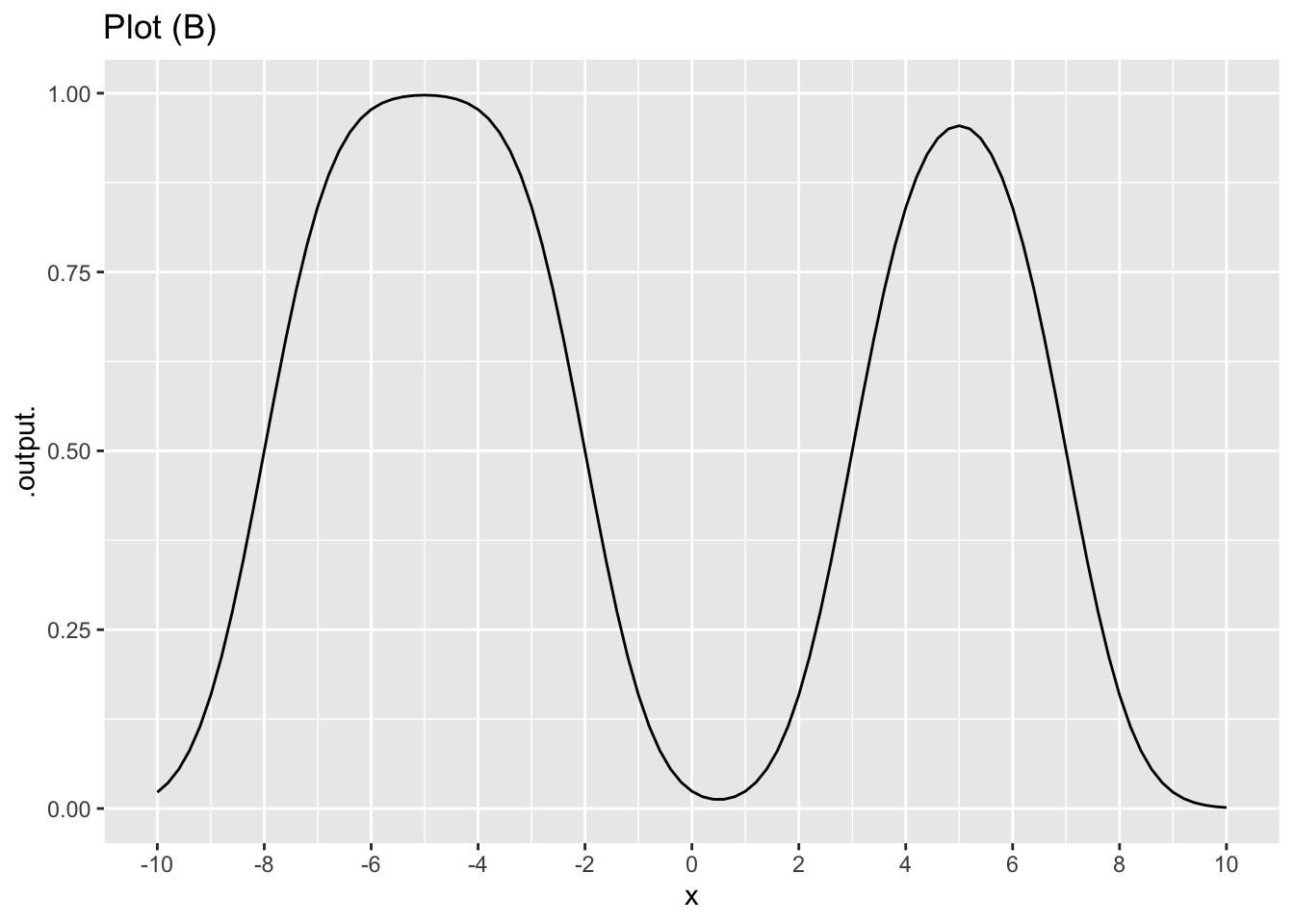
Figure 3: A linear combination of four x-shifted sigmoid functions

In Figure fig-road-1-2 each of the coefficients in the linear combination is either 1 or \(-1\). Recall that a handy fiducial point for the sigmoid function is the input at which the output is 1/2.

  1. Where are the fiducial points for the four sigmoids in Figure fig-road-1-2?

\(-8, -2, 3, 7\)

\(-6, -4, 0, 6\)

\(-9, -8, 1, 5\)

\(-2, 2, 4, 6\)

question id: b-road-1-3

  1. What are the coefficients on the respective sigmoids, in order from the leftmost to rightmost?
\(1, -1, 1, -1\)       \(1, -1, -1, 1\)       \(-1, 1, 1, -1\)       \(-1, 1, -1, 1\)      

question id: b-road-1-4

Exercise 6 The Bargain Basement store wants to sell its goods quickly. Consequently, they reduce each product’s price \(P\) by 5% per day.

  1. If a jacket costs $80 today, how much will it cost in \(t\) days?

\(P = 80 - 5t\)

\(P = 80 - 4t\)

\(P = 80 - 0.05t\)

\(P = 80 (0.05)^t\)

\(P = 80 (0.95)^t\)

question id: chicken-choose-vase-1

Use Active R chunk lst-chicken-choose-vase in answering the next question. Remember, to raise a number to a power, you can use an expression like 0.95^7.

Active R chunk 2
  1. You decided that you like the $80 jacket, but you have a budget of only $60. How long should you wait before coming back to the Bargain Basement store?
3 days       4 days       5 days       6 days      

question id: chicken-choose-vase-2

  1. The answer to question (1) is an exponential function, even if at first it doesn’t look like it. Which of these is the same function but written in the standard \(e^{kt}\) format?

\(80 \exp( \ln(0.95) t)\)

\(0.95 \exp(80 t)\)

\(80 \exp(-\ln(0.95) t)\)

\(0.95 \exp(\ln(80) t)\)

question id: chicken-choose-vase-3

Exercise 7 If you are unlucky and develop a serious ear or throat or other infection, and if the infection is bacterial and not viral, you may be prescribed antibiotics. You probably know how it goes. You go to the pharmacy to pick up a bottle of pills. There might be anywhere between 10 pills and 40. The directions will certainly tell you to make sure to finish the bottle; to take the full course of medication. It may say take a pill twice a day, or three times, or every six hours, perhaps with food.

The details of this regimen are determined largely by the details of whether food inhibits or buffers absorption of the medicine and by the efficiency by which your body metabolizes the medicine and then removes it from your blood via your liver.

Modeling this process—often called the *pharmacokinetics of the drug—is an important step in drug development. A simple but effective model of the drug concentration over time is a piecewise function: zero before you take the pill, then an exponential decay from an initial level of one unit after you take the pill.

Active R chunk 3

The shape of the pill() function is seen in Figure fig-pharma1. Another part of the model is the therapeutic threshold, the minimal concentration for medical effectiveness. Keep in mind that this is a model. In reality, the drug not is absorbed instantaneously as in the model, and the medical effectiveness varies smoothly with concentration rather than being an all-or-nothing affair.

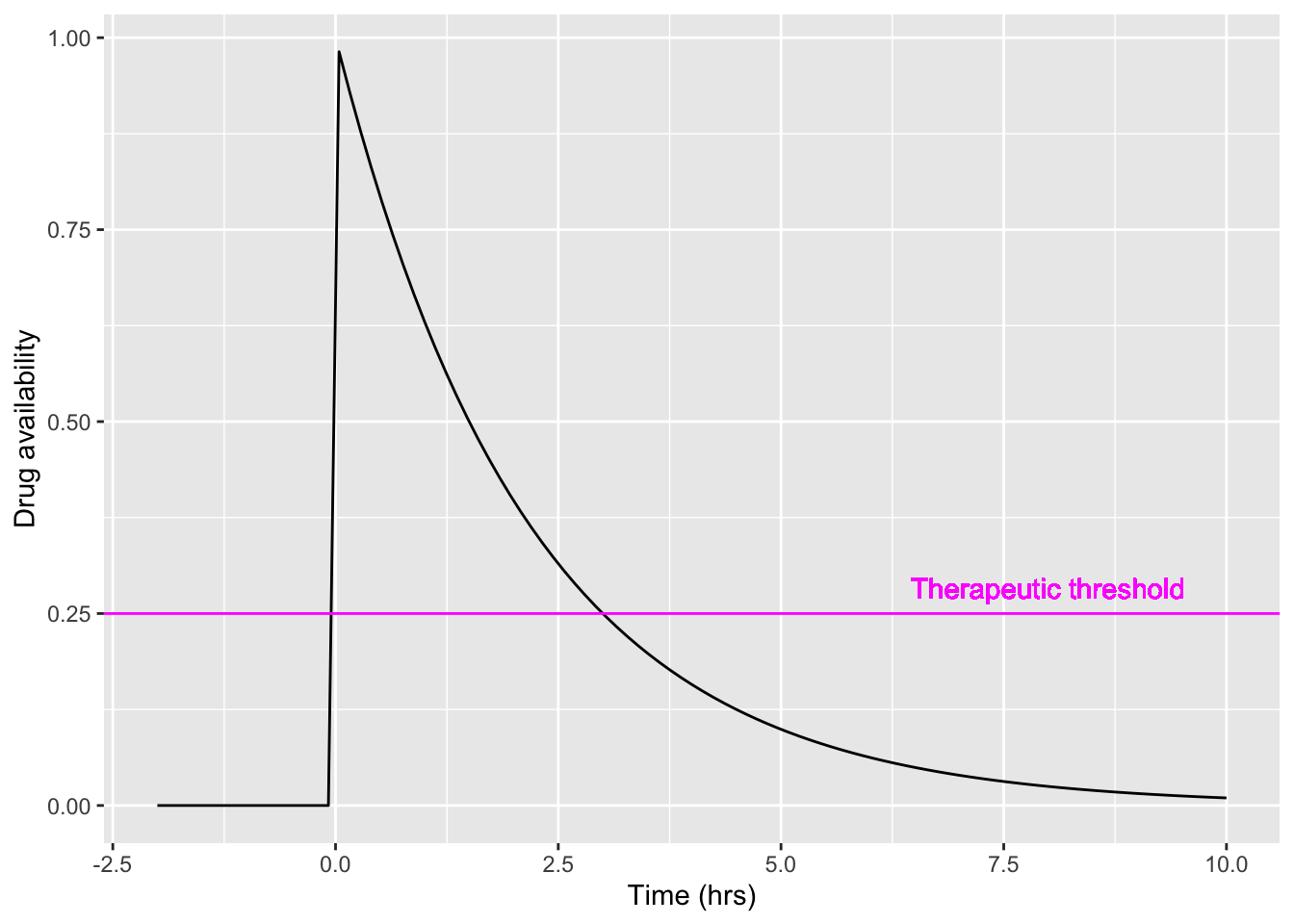
Figure 4: A simple illustrative model of drug availability from taking a unit dose at time zero. The therapeutic threshold depends on the drug: 0.25 is shown here. (The gf_text() function adds a label to the plot. You aren’t expected to master label making.)

The critical features of the model are the half-life of the drug in the body and the therapeutic threshold, both of which depend on the particular drug in question.

  1. What is the half life of the drug depicted in the Figure Figure fig-pharma1?
60 minutes       90 minutes       120 minutes       180 minutes      

question id: goat-walk-window-1

Figure fig-pharma1 shows the availability from a single pill. The goal of taking multiple pills, spread out over time, is to keep the drug availability above the therapeutic threshold for an extended time, e.g. 10 days. There are three parameters to the therapy: how often you take a pill, and the dose delivered by a single pill, and the medicine’s half-life.

  1. Occasionally, the prescription directs you to take a single pill once a day. Suppose the half-life of the medicine is 3 hours. How big would the dose A need to be to keep the availability above a threshold of 0.25 for a 24-hour period?
2 units       16 units       64 units       1024 units      

question id: goat-walk-window-2

Let’s explore a familiar-sounding directive: Take one pill every six hours. We can model this by a linear combination of time-shifted pill() functions. Each pill provides a dose of size A.

Note: Remember to run Active R chunk lst-define-pill-goat before running Active R chunk lst-goat-walk-window-six and Active R chunk lst-goat-walk-window-eight:

Active R chunk 4

The graph shows that the drug is above the therapeutic threshold (0.25) for the entire first day (0-24 hours).

  1. From the graph of drug availability versus time, do you think continuing the one-pill-every-6-hours regimen will continue to keep the drug level over the therapeutic threshold for the remainder of the course of treatment? Explain why or why not.

question id: goat-walk-window-3

Let’s switch to an one-pill every 8 hour regimen, the pills being taken at midnight, 8am, and 4pm, …

  1. How big a dose A will be needed to keep the drug availability above the therapeutic threshold for the entire course of treatment? (Hint: Construct a function analogous to six_hours() that simulates a pill every 8 hours. Plot out the drug availability over the 24 hours of the first day. Then vary the dose A until you find the minimum dose that keeps the availability over the threshold of 0.25 for the entire day.)
0.4 drug units       0.6 drug units       1.3 drug unit       1.9 drug units       2.1 drug units      

question id: goat-walk-window-4

Active R chunk 5
  1. Suppose the instructions were to take 2 pills when you start treatment and then an additional pill every 8 hours. How big a dose A would be needed to keep the drug availability above the therapeutic threshold for the entire course of treatment?
0.2 drug units       0.7 drug units       0.9 drug unit       1.1 drug units      

question id: goat-walk-window-5

  1. Which of the three regimens described (6-hour, 8-hour, 8-hour-double-first-dose) involves the smallest total dose? (The total dose is the sum of the doses for each pill administration.)
6-hour regimen       8-hour regimen       Start with 2 pills then take 1 pill every 8-hours.      

question id: goat-walk-window-6

Exercise 8  

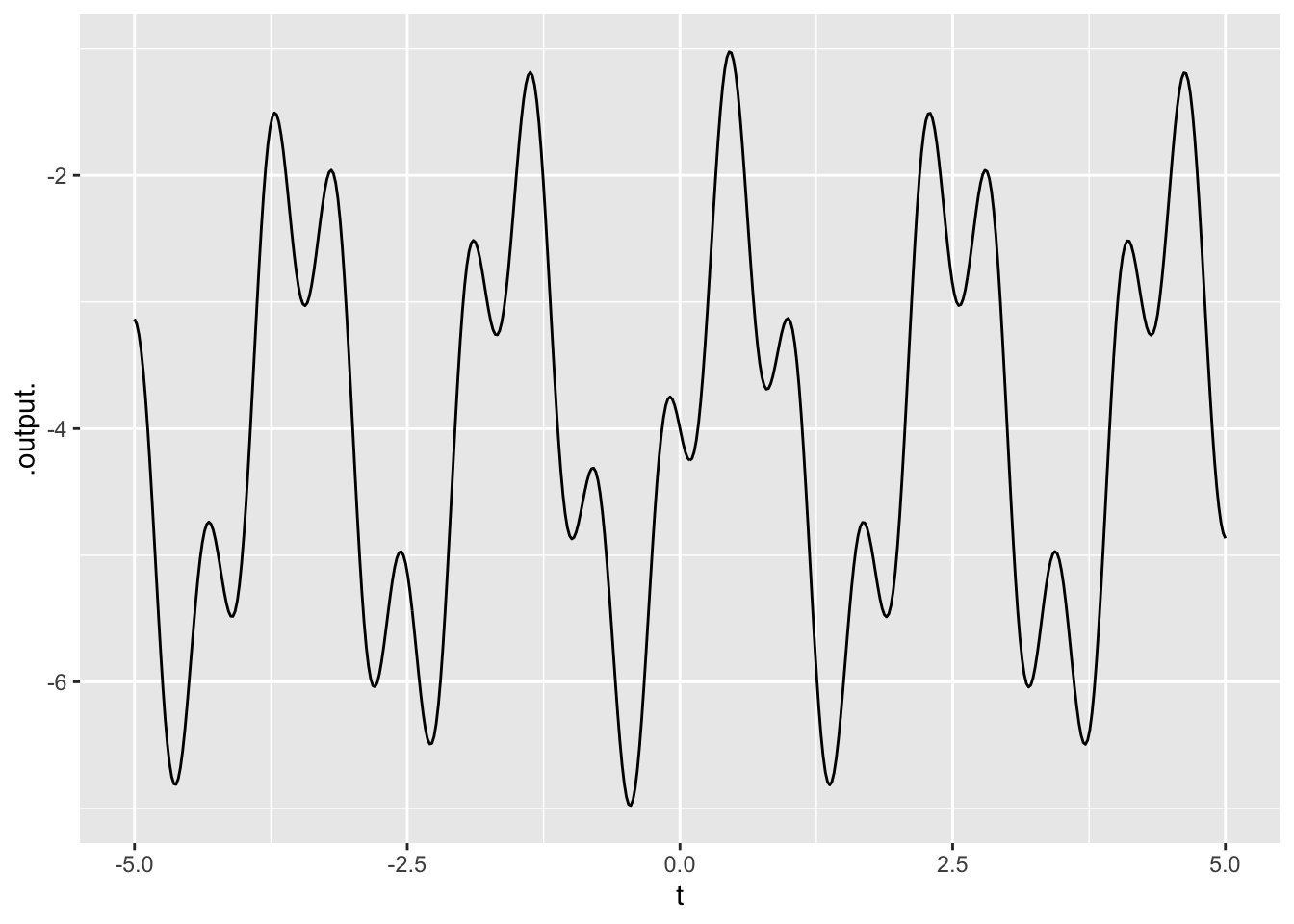
Figure 5: Linear combination of two sinusoids, one of period 0.6 and the other of period 2. There is also a baseline shift. The formula is in Math expression eq-two-sines-eq.

\[A_1 \sin\left(\frac{2\pi}{2}t\right) + A_2 \sin\left(\frac{2\pi}{0.6} (t-.3)\right) + A_3 \tag{1}\]

  1. What is \(A_3\)?
-4       -2       0       2       4      

question id: two-sines-1a

  1. What is \(A_1\)?
0       1       2       3.5      

question id: two-sines-1b

  1. What is \(A_2\)?
0       1       2       3.5      

question id: two-sines-1c

Exercise 9 Figure fig-two-gaussians shows two gaussian functions \(g_1(t)\) and \(g_2(t)\) with different means and standard deviations.

Figure 6: Two gaussian functions

Figure 7: A linear combination of the two functions in Figure fig-two-gaussians.
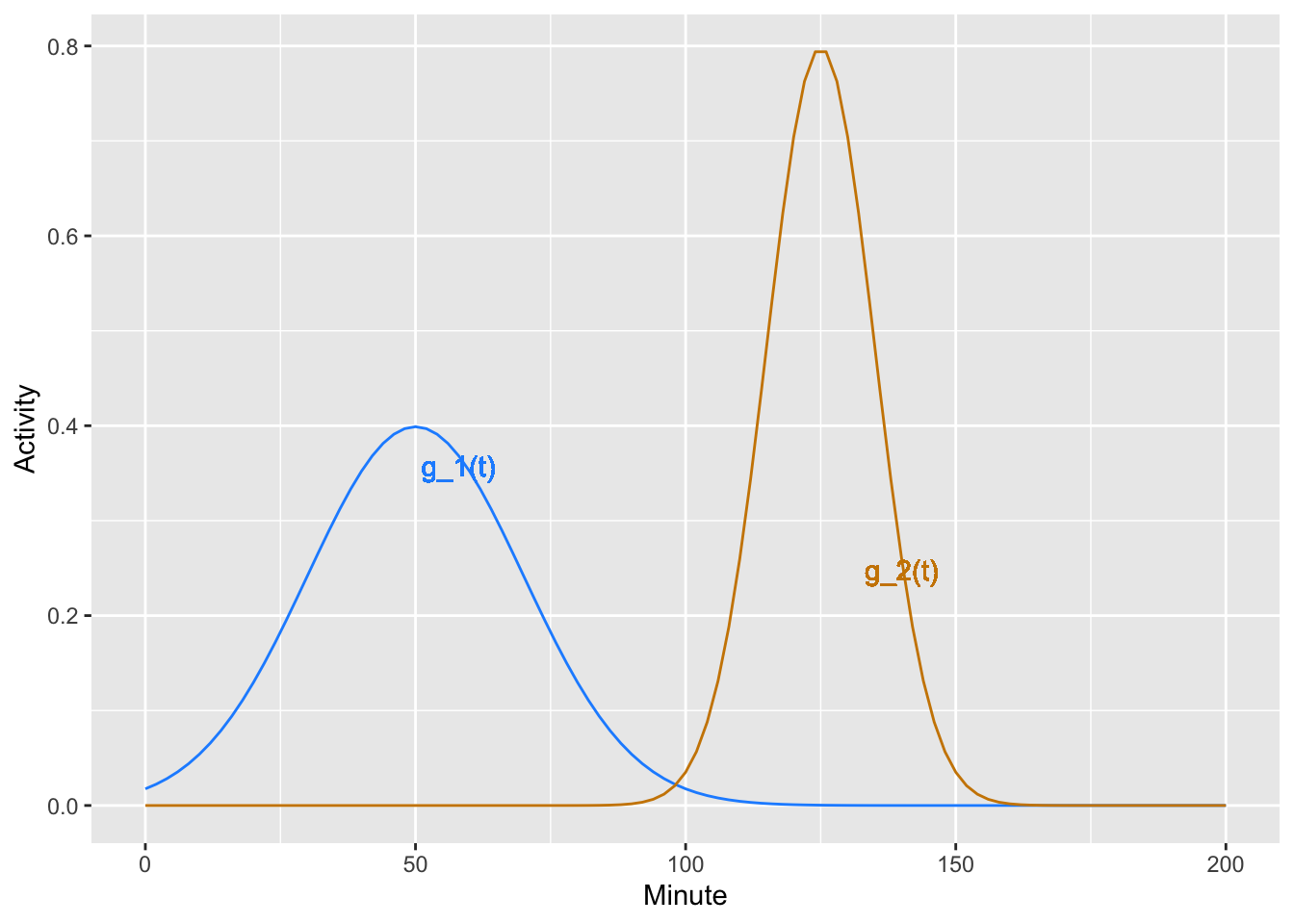
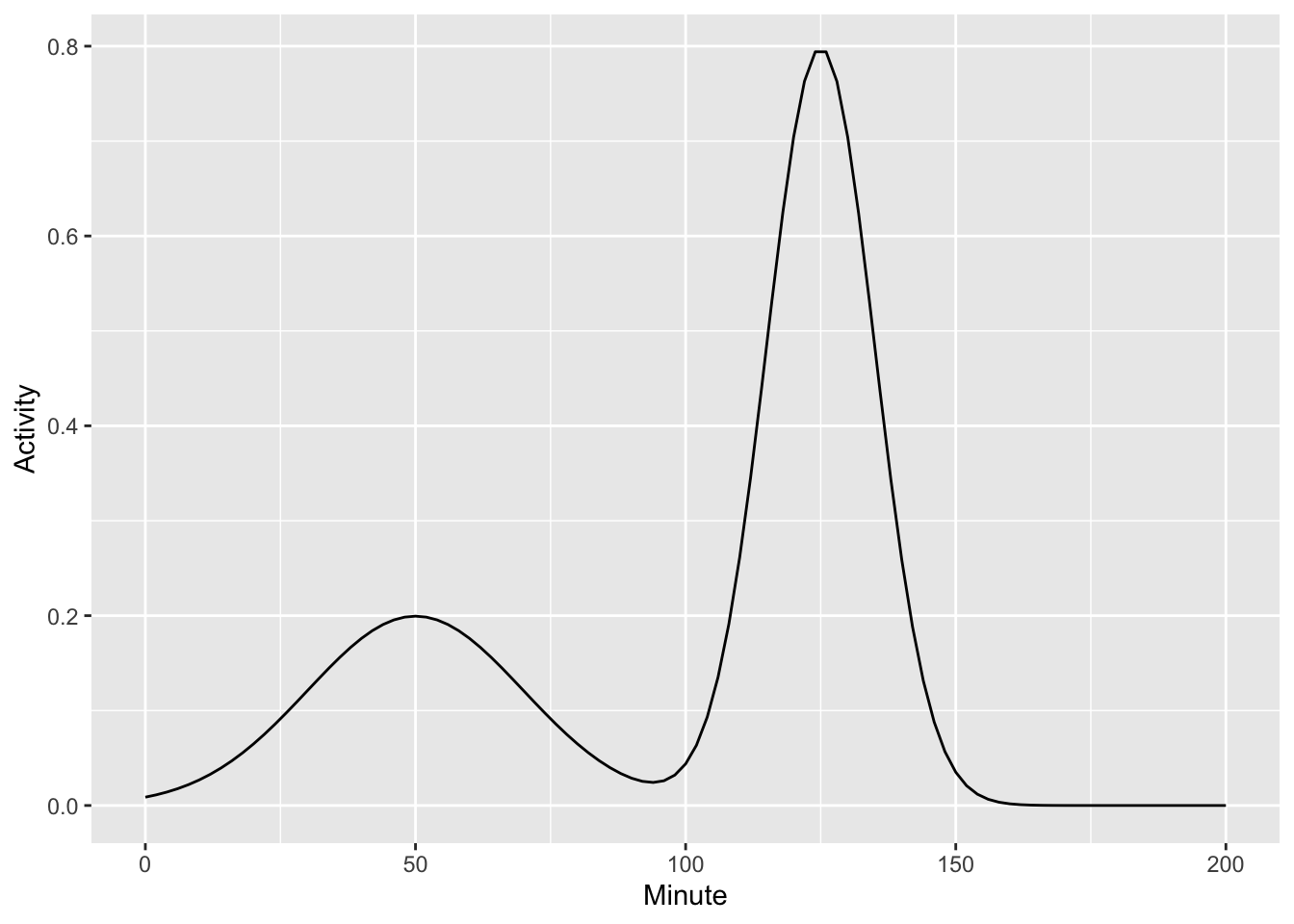
  1. What is the linear combination of \(g_1(t)\) and \(g_2(t)\) shown in Figure fig-combination-A?

\(0.5\,g_1(t) + g_2(t)\)

\(g_1(t) + 0.25\,g_2(t)\)

\(g_1(t) + 2\,g_2(t)\)

question id: daily-digital-09-QA17

Figure 8: Another linear combination of the functions in Figure fig-two-gaussians.
  1. Which linear combination of \(g_1(t)\) and \(g_2(t)\) is shown in Figure fig-combination-B?

\(g_1(t) - 2\, g_2(t)\)

\(g_1(t) - g_2(t)\)

\(0.5\,g_1(t) - 0.5\, g_2(t)\)

\(-g_1(t) - g_2(t)\)

question id: daily-digital-09-QA18

Exercise 10  

Figure 9: .
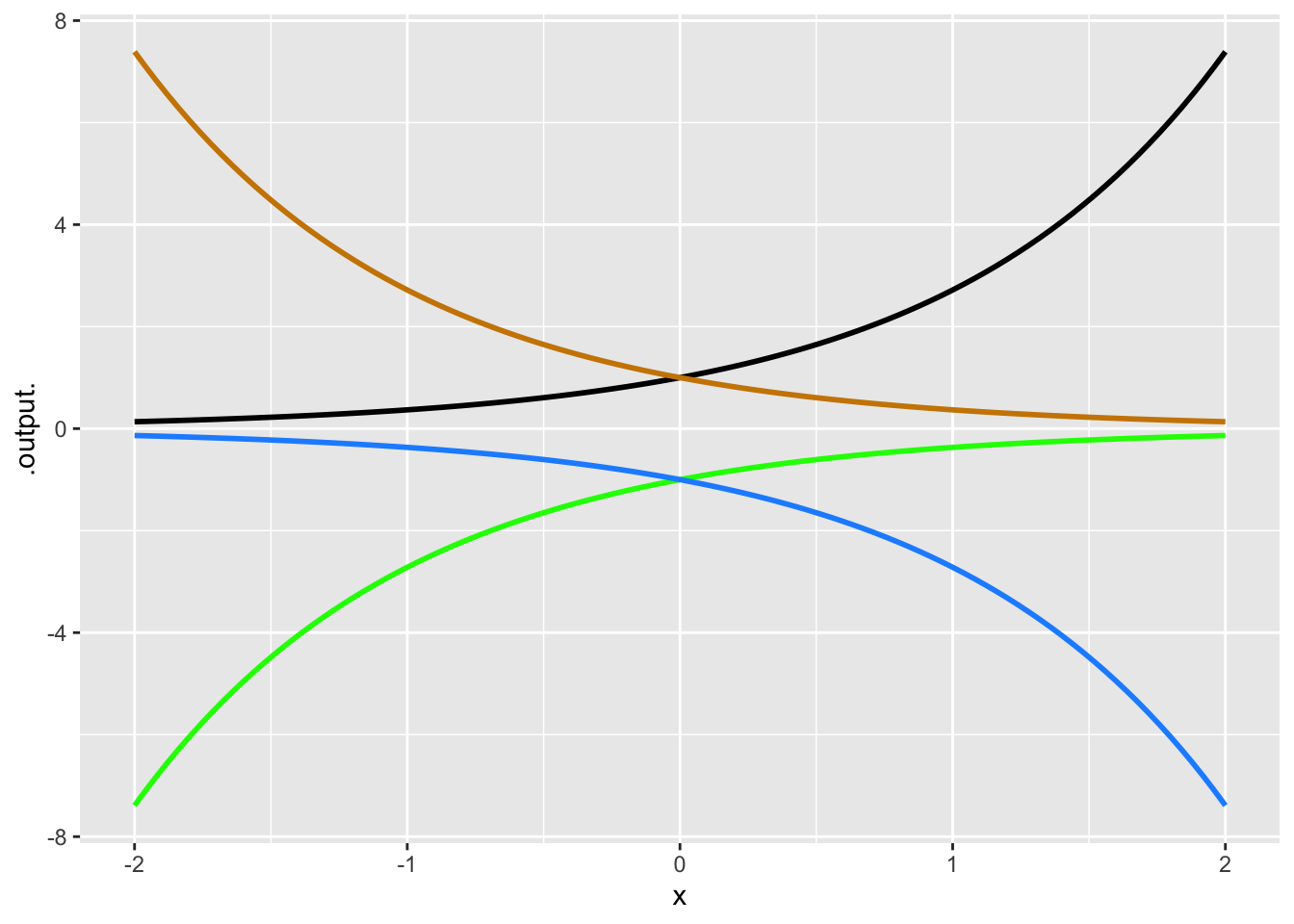
  1. One of the curves in Figure fig-flipping-1-1 is a pattern-book function. Which one?
black       blue       green       tan       none of them      

question id: flipping-1-1a

  1. Taking \(f()\) to be the pattern-book function in Figure fig-flipping-1-1, which one of the curves is \(f(-x)\)?
black       blue       green       tan       none of them      

question id: flipping-1-1b

Figure 10: .
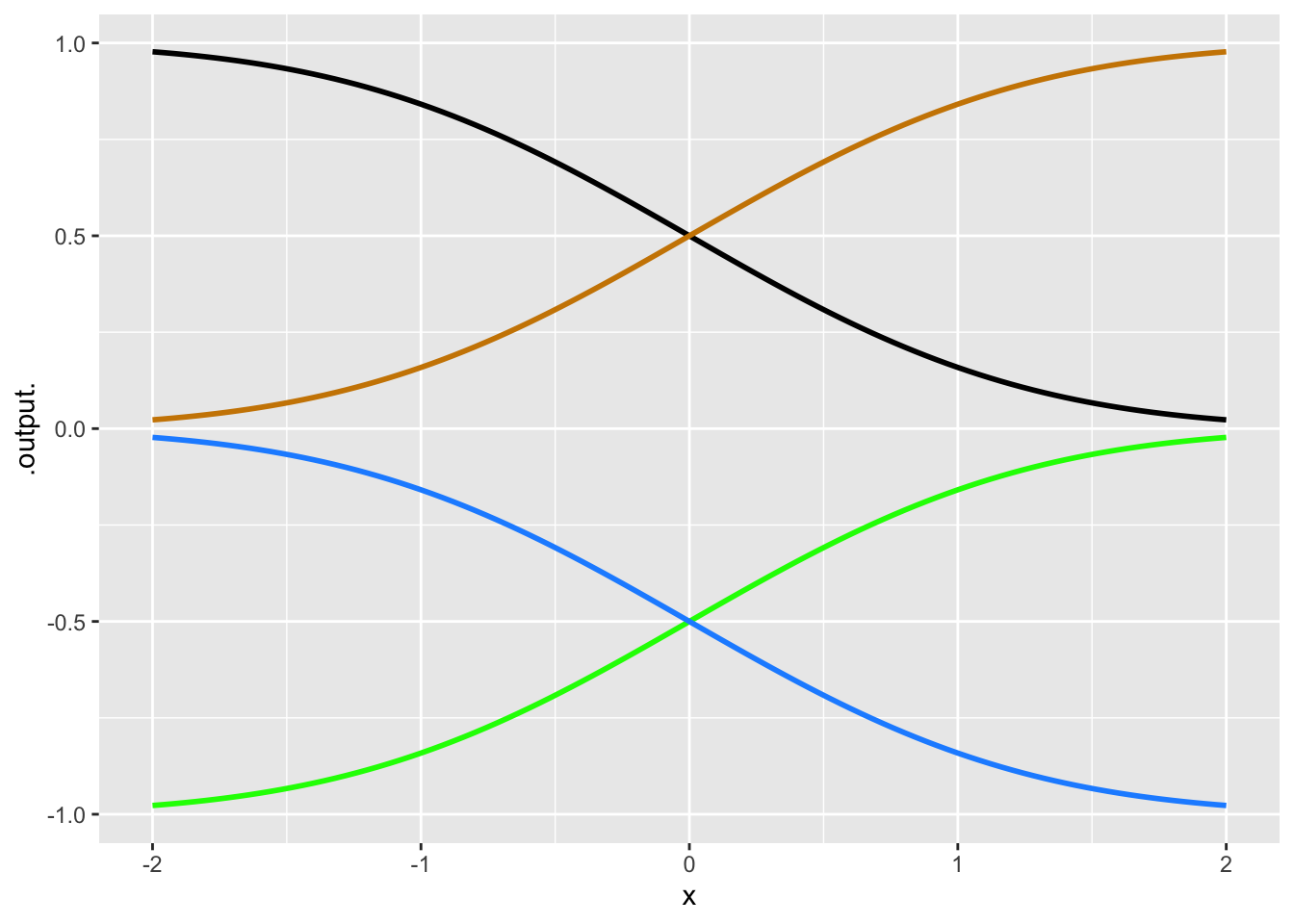
  1. One of the curves in Figure fig-flipping-1-2 is a pattern-book function. Which one?
black       blue       green       tan       none of them      

question id: flipping-1-2a

  1. Taking \(f()\) to be the pattern-book function in @flipping-1-2, which one of the curves is \(-f(x)\)?
black       blue       green       tan       none of them      

question id: flipping-1-2b

Figure 11
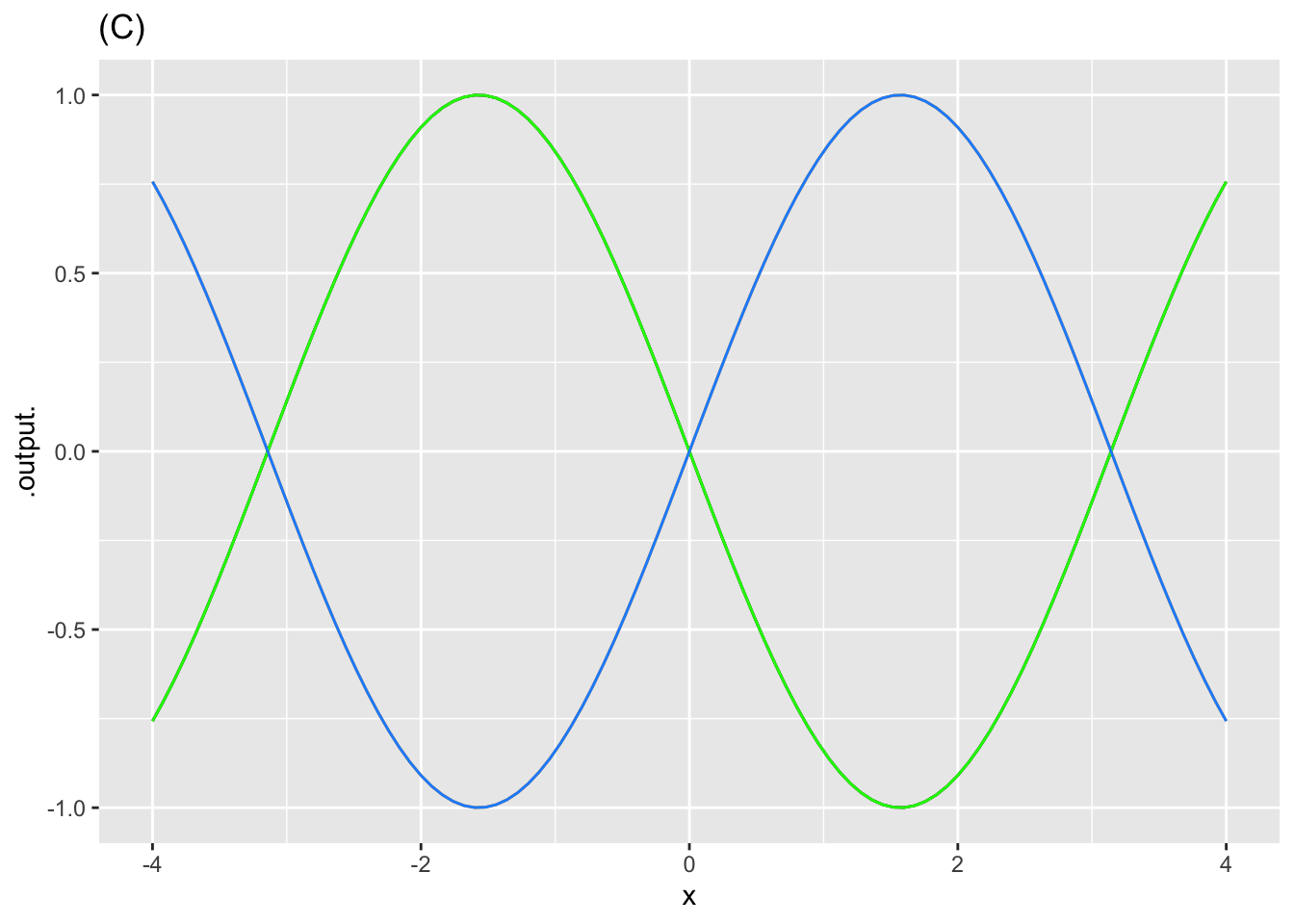
  1. The blue curve in Figure fig-flipping-1-3, as you know, is the sinusoid pattern-book function. Which of these functions is the green curve?

\(\sin(-x)\)

\(-\sin(x)\)

\(-\sin(-x)\)

Both \(\sin(-x)\) and \(-\sin(-x)\)

Both \(\sin(-x)\) and \(-\sin(x)\)

question id: flipping-1-3a

Figure 12
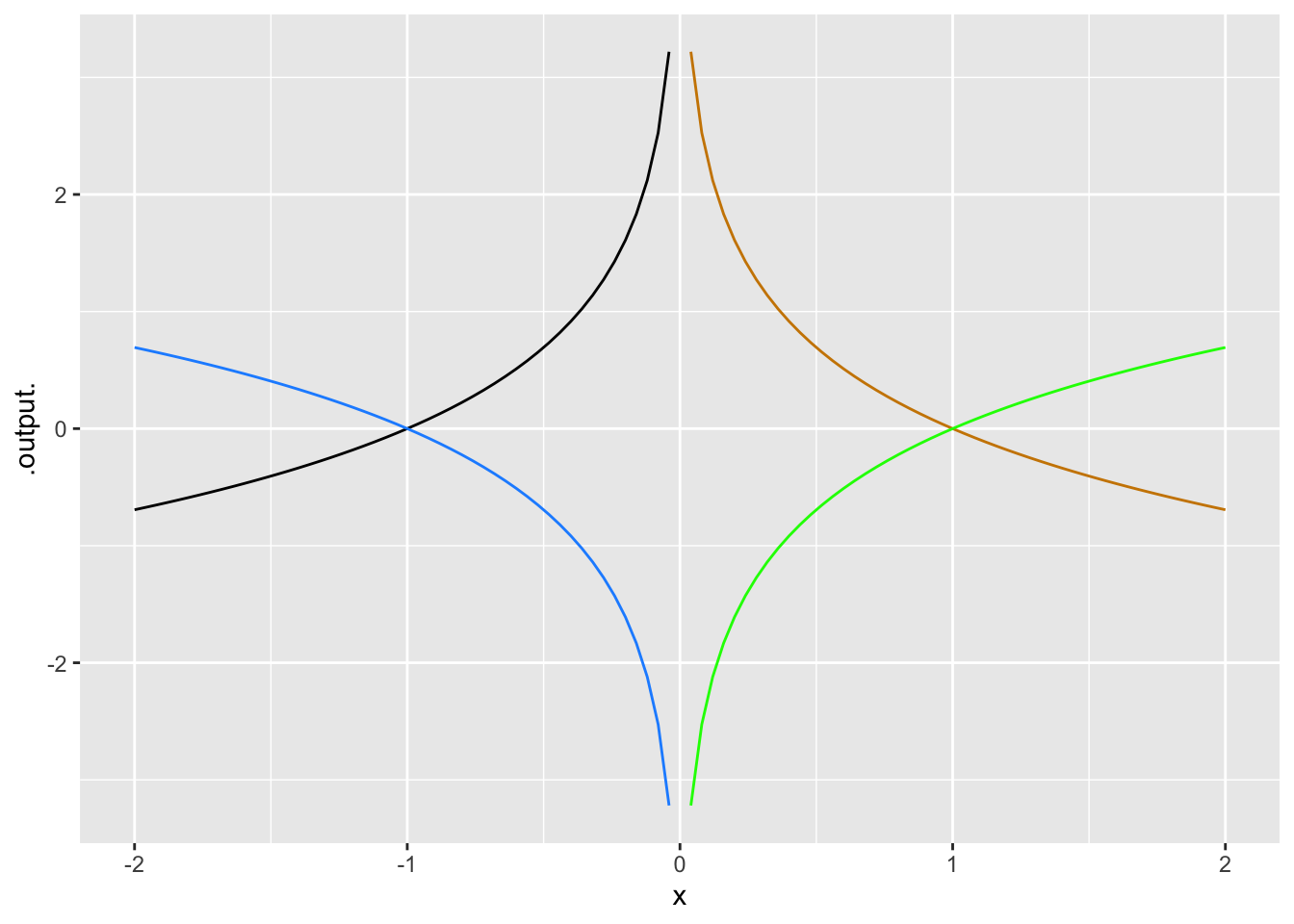
  1. One of the curves in Figure fig-flipping-1-4 is a pattern-book function. Which one?
black       dodgerblue       green       tan       none of them      

question id: flipping-1-4a

  1. Taking \(f()\) to be the pattern-book function in Figure fig-flipping-1-4, which one of the curves is \(-f(-x)\)?
black       dodgerblue       green       tan       none of them      

question id: flipping-1-4b

Exercise 11 Here is an interactive R chunk to use in answering the following questions:

  1. What is the shape of the graph of the composition \(\pnorm(\pnorm(x))\)?
a sigmoid       a gaussian       an exponential      

question id: compose-1-1

  1. What is the shape of the graph of the composition \(\pnorm(\dnorm(x))\)?
a sigmoid       a gaussian       an exponential      

question id: compose-1-2

  1. What is the shape of the graph of the composition \(\dnorm(\pnorm(x))\)?
a sigmoid       a gaussian       an exponential      

question id: compose-1-3

  1. What is the shape of the graph of the composition \(\ln(\dnorm(x))\)?
a sharp rise from (0,0) followed by an asymptotic approach to 0 as \(x\rightarrow \infty\)       a fishhook       a parabola      

question id: compose-1-4

  1. What is the shape of the graph of the composition \(\ln(x^2)\)?
similar to the log function itself       a gaussian function       a sigmoid      

question id: compose-1-5

  1. What is the shape of \(\exp(x^2)\)?
U-shaped       V-shaped       W-shaped       a gaussian function      

question id: compose-1-6

U-shaped       V-shaped       W-shaped       a sigmoid function      

question id: compose-1-7

  1. What is the shape of \(\exp(-x^2))\)?
U-shaped       V-shaped       W-shaped       a gaussian function      

question id: compose-1-8

  1. What is the range of \(\sin(1/x)\)?

\(-1 \leq \sin(1/x) \leq 1\)

\(\infty < \sin(1/x) < \infty\)

\(0 \leq \sin(1/x) < \infty\)

\(-\infty < \sin(1/x) \leq 1\)

question id: compose-1-9

  1. What is the range of \(1/\sin(x)\)?

\(-1 \leq | \sin(1/x) |\)

\(\infty < \sin(1/x) < \infty\)

\(0 \leq \sin(1/x) < \infty\)

\(-\infty < \sin(1/x) \leq 1\)

question id: compose-1-10

  1. What is the shape of the graph of the composition \(\ln(\pnorm(x))\)?

a rise followed by an horizontal asymptotic approach to 0 as \(x\rightarrow \infty\)

a fishhook

a parabola

question id: compose-1-11

Exercise 12 Figure fig-inverse-square-law shows how the intensity of light from the sun depends on distance \(r\). Wikipedia link The intensity is the number of photons per unit area. Imagining each red line to be the path followed by one photon, the intensity can be calculated by the area of the surfaces at distance \(r\), \(2r\), and \(3r\).

Figure 13

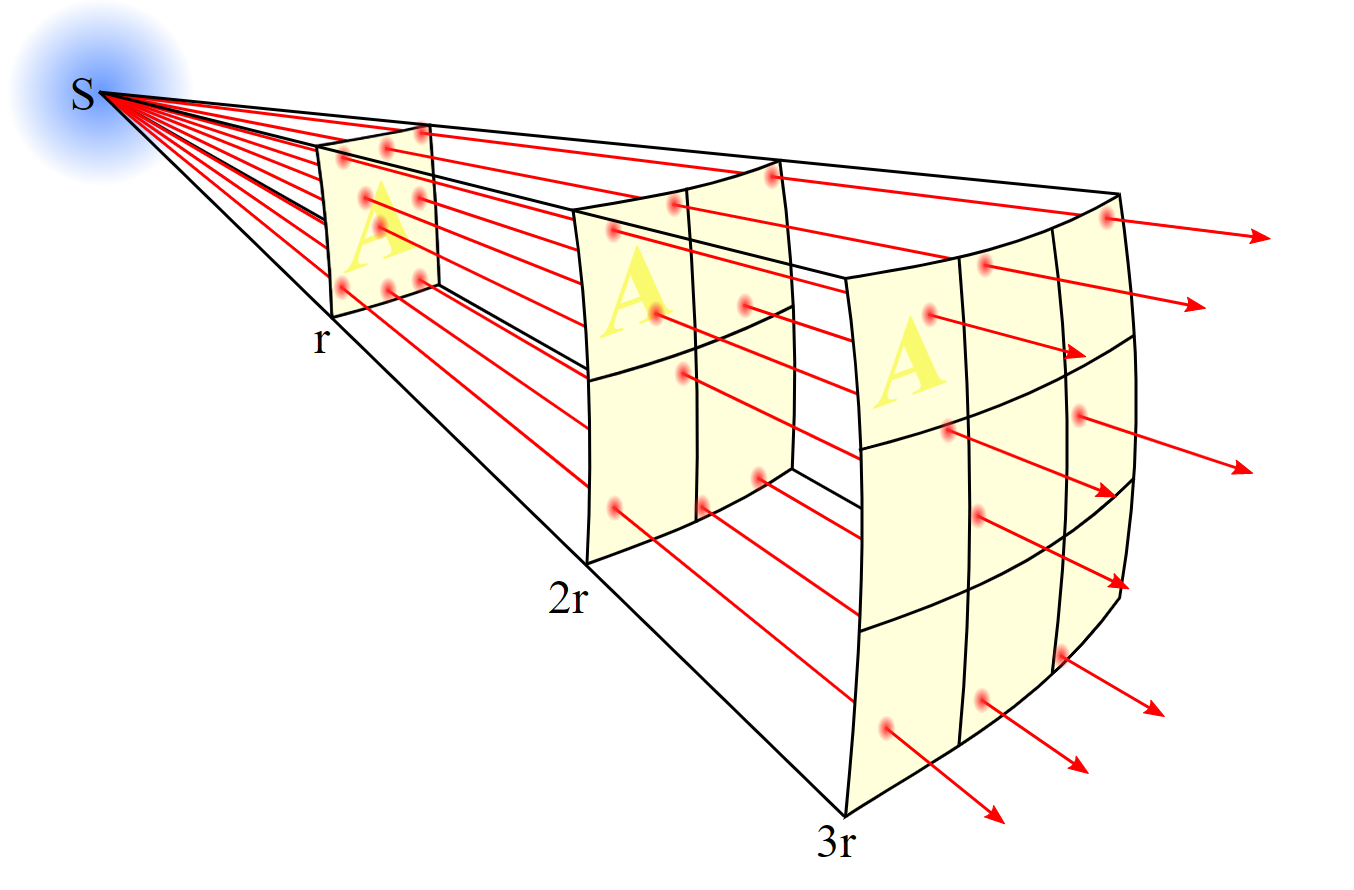
Which of these functional forms best models intensity \(\cal I\) as a function of distance \(r\)?

Proportional: \(\cal I(r)\equiv ar+b\)

Power-law: \(\cal I(r)\equiv Ar^p\)

Exponential \(\cal I(r)\equiv Ae^{kr}+C\)

Sine: \(\cal I(r)\equiv A\sin \left(\frac{2\pi}{p}(r-r_0)\right)+B\)

Sigmoid \(\cal I(r)\equiv A\cdot \pnorm(r,mean,sd)+B\)

Gaussian \(\cal I(r)\equiv A\cdot \dnorm(r,mean,sd)+B\)

question id: dolphin-burn-clock-1

Exercise 13 According to data from the US National Health and Nutrition Evaluation Survey, the average height of adult females is 157 cm vs 167 for adult males. The standard deviations are 17 cm and 22 cm respectively. A good model for the person-to-person variation for females is dnorm(height, mean = 157, sd = 17) and similarly for males.

To see the overall distribution of adult height, regardless of sex, make a linear combination of the distribution for females and for males, giving each a scalar of one-half (since the population is roughly 50-50 female/male).

In the interactive R chunk, construct the linear combination function for the overall distribution. Use the scaffolding to plot out the distributions for the individual sexes and the overall distribution.

Some people erroneously think that since the mean height of men is larger than women by 10cm, you can readily distinguish between the sexes based on height. However, notice that the overall distribution (plotted in black) does not show a dip between the sexes: there is no clear separation based on height.

As a thought experiment, let’s increase the separation in mean height from the actual value of \(167-157=10\) cm to something larger. You can increase the separation by 5 cm, for example, by making the men’s mean height 167+5.

What’s the smallest increase in separation (in cm) that produces a barely visible dip between the sexes in the overall height distribution?

5       10       15       20       25       30      

question id: tg4

Exercise 14 The data points in Active R chunk lst-keplers-distance-mars were collected by astronomer Tycho Brahe (1546-1601) and used by Johannes Kepler (1571-1630) to develop his theory of the motion of planets. The data record the estimated distance from Mars to the Sun as a function of time. They are not a continuous record because Mars can’t be observed when it is on the other side of the Sun from Earth.

The function that Kepler wanted to fit to the data is

\[dist(t) \equiv A \sin\left(2\pi (t - t_0 \right)/P + B \tag{2}\]

Math expression eq-input-output-scaled-sin has two coefficients, \(A\) and \(B\), as well as two nonlinear parameters \(P\) and \(t_0\).

The code in Active R chunk lst-keplers-distance-mars plots Kepler’s data along with a very poorly fitting model.

Active R chunk 6

Ignore for the moment the nonlinear parameters, that is, the period and time shift of the sinusoid.

Good values for the linear coefficients \(A\) and \(B\) can be estimated by eye. Modify the \(A\) and \(B\) parameters to produce a sinusoid that nicely covers the range of the data.

I confirm honorably that I have found nice \(A\) and \(B\) parameters.

I haven’t had the chance yet to complete this task.

question id: kepler-linear

Nonlinear parameters are much harder to find. Try to figure out values for \(P\) and \(t_0\) that bring the model function into close alignment with the data. Hint: The collected data cover every orbit of Mars during the time span in the graphical domain, so a good first guess is to look at the time difference between successive clusters of data points.

I confirm honorably that I have found pretty reasonable \(P\) and \(t_0\) parameters.

I haven’t had the chance yet to complete this task.

question id: kepler-nonlinear

Exercise 15 Epidemics are often modeled as a series of “waves.” Each wave involves different people. Let’s imagine two epidemic waves, one passing through the “blue” population and a smaller one through the “orange” population, like this:

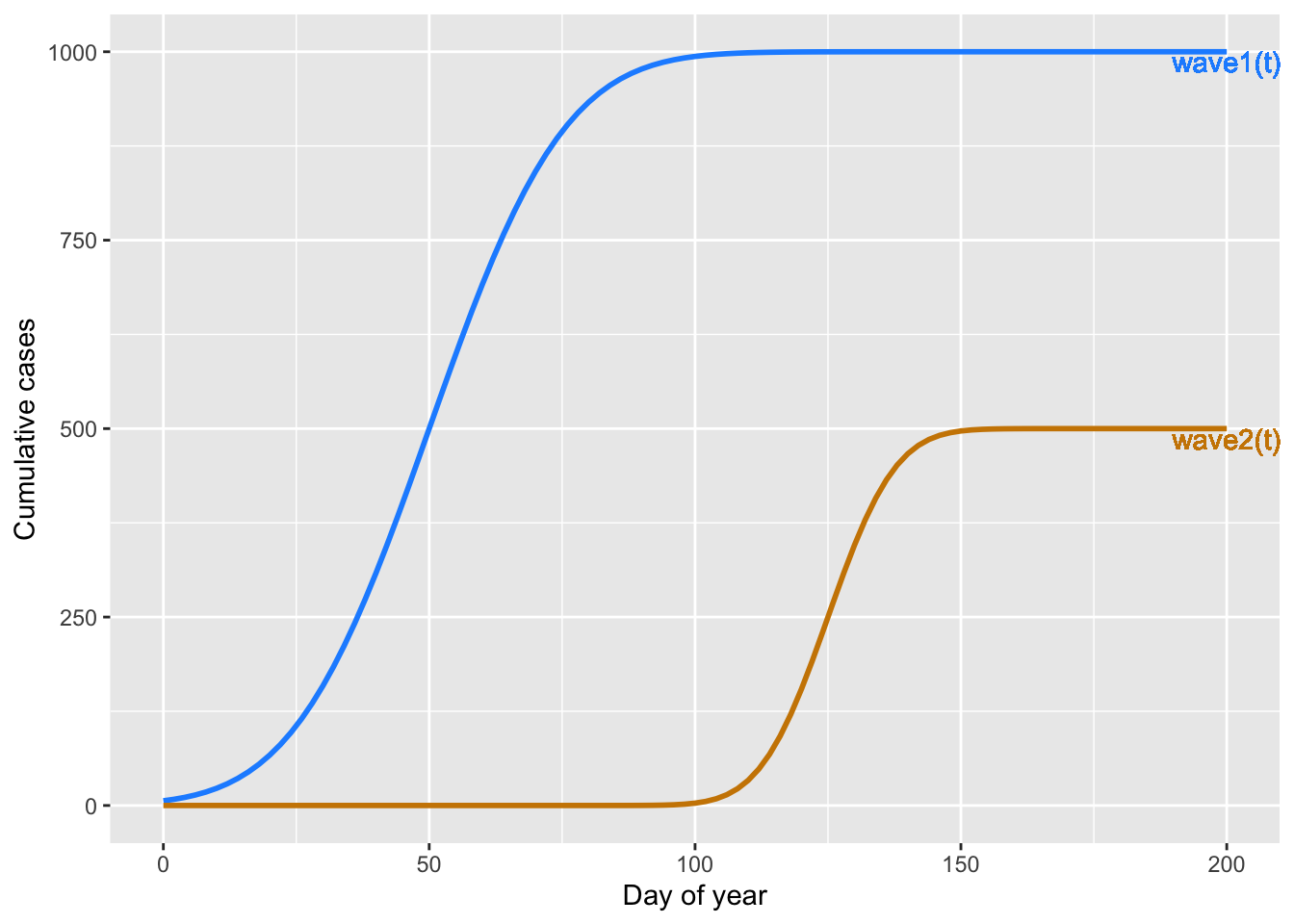
Figure 14: Accumulated number of cases as an epidemic passes through two distinct populations.

Assuming that there were no way to distinguish between red and blue cases, that is, if the populations were not distinct, the epidemic would look like just one curve. Figure fig-arith-with-funs2 shows four different candidates for this curve.

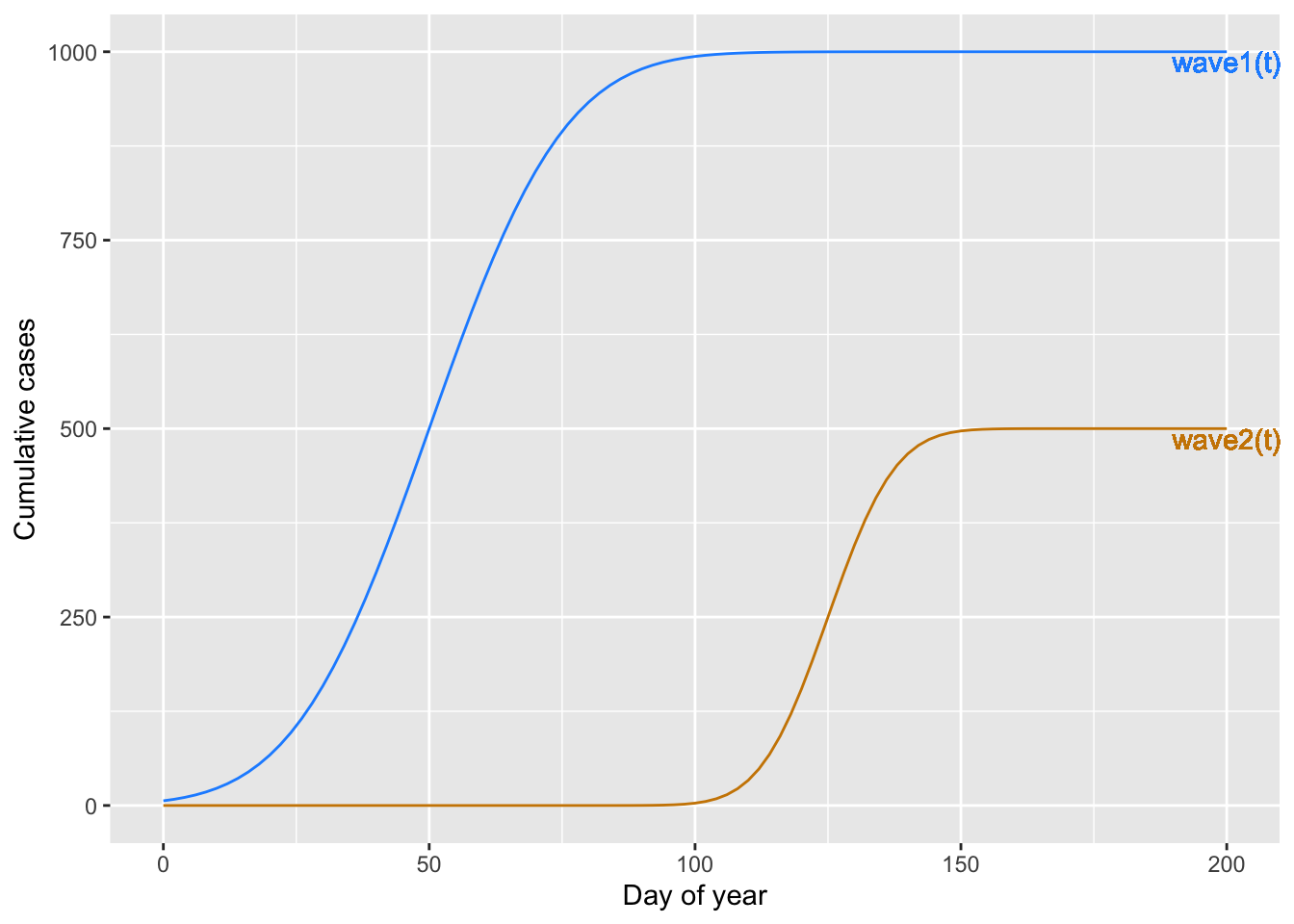
Figure 15: Four possible curves to consider when answering the following questions.
  1. Which of the following curves would the overall epidemic look like? (The colors are just to help you distinguish the different functions)
A       B       C       D      

question id: daily-digitial-09-QA14

  1. Which of the following curves would the overall epidemic look like? (The colors are just to help you distinguish the different functions)
A       B       C       D      

question id: daily-digital-09-QA15

Each of the functions shown in Figure fig-arith-with-funs2 is a “linear combination” of the red function and the blue function. The real total cumulative cases is “wave1(t)” plus “wave2(t)”. The other functions are made up and are irrelevant to the real epidemic. Still, we can ask what arithmetic combination of “wave1(t)” and “wave2(t)” was used to create the made-up function.

  1. For made-up function (A) in the graph, what was the linear combination?

1000 - wave1(t) + wave2(t)

2 wave1(t) - 3 wave2(t)

1000 + wave1(t) - wave2(t)

question id: daily-digital-09-QA16

Exercise 16 The graph shows (in black) a function constructed as the product of two basic modeling functions. The graph also shows a pair of blue curves that encompass the black function. These are called the envelope of the black function.

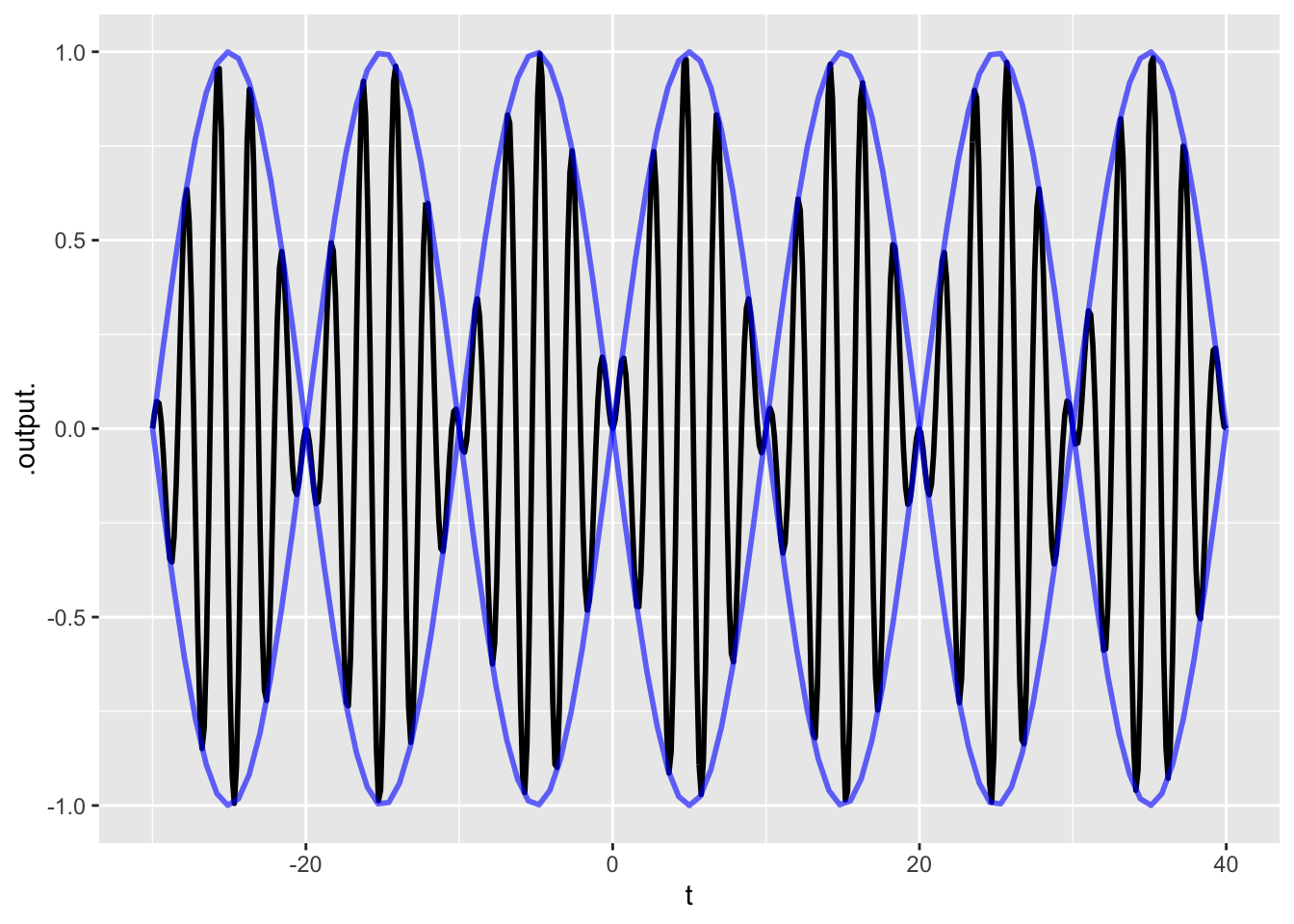
  1. What are the two basic modeling functions being multiplied?

A sinusoid and another sinusoid with a faster period.

A gaussian and a sinusoid.

A sigmoid function and a sinusoid.

question id: sin-in-sin-1

  1. What are the two basic modeling functions being multiplied?

A sinusoid and another sinusoid with a faster period.

A gaussian and a sinusoid.

A sigmoid function and a sinusoid.

question id: sine-in-sine-2

  1. What is the period of the envelope?
10       20       30      

question id: sine-in-sine-3

Exercise 17 Here, in traditional mathematical notation, are the equations for calculating the length of daylight as a function of latitude and day number (1-365). First you calculate \(y()\), then the solar declination, then the hour-angle, then use the result to find the length of daylight.

\[y(\text{day}, \text{hour}) \equiv (2\pi/365) \times(\text{day} - 1 + (\text{hour}-12)/24)\]

\[\text{declination}(y) \equiv 0.006918-0.399912\,\cos(y)+0.070257\,\sin(y)-0.006758\,\cos(2*y)+0.000907\,\sin(2*y)-0.002697\,\cos(3*y)+0.00148\,\sin(3*y)\]

\[\text{hour_angle}(L, \delta) \equiv \text{acos} \left(\strut\cos(90.833) /(\cos(L) \cos(\delta)) - \tan(L)\tan(\delta)\right)\] where \(\delta\) is the solar declination.

\[\text{daylight_length}(\text{hour_angle}) = 2 \ \text{hour_angle}(L, \delta) \ / 15\]

Use Active R chunk lst-april-fools to implement these four functions in R. (The trig functions are spelled the same in R as in traditional notation.)

Active R chunk 7

You will need to put these four functions together for the final calculation of daylight length. Active R chunk lst-april-fools-2 shows how.

Active R chunk 8

How long is the day on April Fools Day (\(n=90\)) at Latitude 39\(^\circ\)N? (Use

12.38 hours       12.59 hours       12.64 hours       12.74 hours      

question id: april-fools

Exercise 18 It is very common in communications systems to have a signal that is a sine-wave carrier that is modulated by another function. That is, the carrier is multiplied by the other function: waveform(t) = modulator(t) \(\times\) carrier(t).

The interactive R chunks each have an examples in which a sine with a period of about 2 units is modulated by another function. In each case, that other function is one of the modeling functions we have studied.

Active R chunk 9
  1. Of what sort is the function that is modulating the carrier?
exponential       gaussian       sigmoid       sine      

question id: dd-09-a

Active R chunk 10
  1. Of what sort is the function that is modulating the carrier?
exponential       gaussian       sigmoid       sine      

question id: dd-09-b

Active R chunk 11
  1. Of what sort is the function that is modulating the carrier?
exponential       gaussian       sigmoid       sine      

question id: dd-09-c

Active R chunk 12
  1. Of what sort is the function that is modulating the carrier?
exponential       gaussian       sigmoid       sine      

question id: dd-09-d

:::

Exercise 19 Recall the Pythagorean theorem: \(C^2 = A^2 + B^2\). Let’s write this as a function that takes as inputs the lengths of the two legs and produces as output the length of the hypotenuse.

\[\text{hypotenuse}(a, b) \equiv \sqrt{\strut a^2 + b^2}\]

This can be seen as a composition of a function \(f(x) \equiv \sqrt{x}\) into a linear combination of square functions of different inputs: \(g(a, b) \equiv a^2 + b^2\).

  1. What is the function \(f()\)?

\(f(x) \equiv a^2\)

\(f(x) \equiv \sqrt{x}\)

\(f(x) \equiv x^2\)

\(f(x) \equiv +\)

question id: py2-1

  1. What is the function \(g()\)?

\(g(x) \equiv a^2\)

\(g(a) \equiv x^2\)

\(g(x) \equiv x^2\)

\(g(x) \equiv a^2 + b^2\)

question id: py2-2

  1. There are two functions in the linear combination. What are they?

\(g(a)\) and \(g(b)\)

\(f(x)\) and \(g(x)\)

\(f(b)\) and \(g(b)\)

question id: py2-3

  1. What are the scalars in the linear combination?
\(1\) and \(1\)       \(1\) and \(-1\)       There are no scalars.      

question id: py2-4

Why are \(a\) and \(b\) inputs to hypotenuse, not parameters?

You used \(a\) and \(b\) as the names of the inputs to hypotenuse(). Aren’t \(a\) and \(b\) meant to be parameters, not input names?

You can use whatever you want as input names, so long as they are used consistently between the left and right sides of the \(\equiv\). Names like \(x\), \(t\), and \(y\) scream out to be recognized as input names, so these are what we use most of the time. But the Pythagorean theorem is usually written using A, B, and C. I’m honoring that convention so that a human reader gets a cultural hint what the inputs stand for. I’m unapologetic about this, since you got fair warning by the left side of the \(\equiv\) what the argument names are.

Activities

Exercise 20  

Figure 16: Power produced by the author’s rooftop photovoltaic array in June 4 (solid line) and June 3 (bars), 2022.

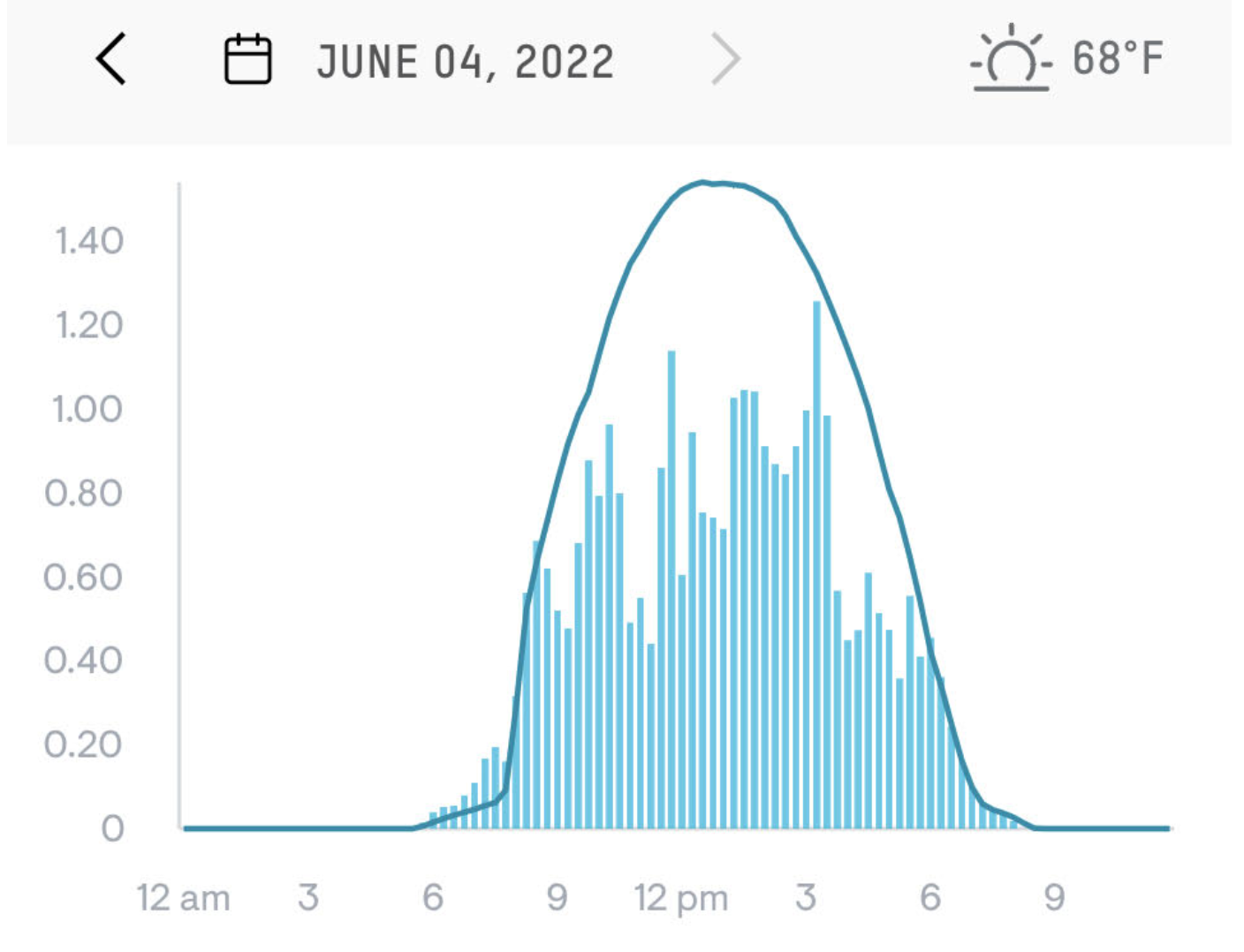
Figure fig-solar-june comes from the monitoring app for a photovoltaic (solar electricity) array on two consecutive days in June 2022. The vertical axis is in kilowatts (power). The overall pattern for June 4 is a bump function with a peak around 13:00 falling to zero at 6am and 9pm. (13:00 is roughly solar noon, due to daylight savings time.) We’ll call this function sun(t). June 3 shows a more complex pattern, due to passing clouds that diminish the available sunlight.

A reasonable model for the June 3 pattern is the bump function sun(t) multiplied by an irregular function of time representing the clouds. Let’s call it cloudiness(t), imagining that the range is from 0 (dark, obscuring clouds) to 1 (no clouds at all). The power produced is therefore

power(t) \(\equiv\) solar(t) \(\times\) cloudiness(t)

Refering to Figure fig-solar-june, sketch out the graph of cloudiness(t) for June 3.

No answers yet collected