Chap 6 Review

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1 What is the value of \(f(4)\) when \(f(x) \equiv 2 x + 1\ ?\)

-2       -4       2       4       9      

question id: drill-M01-4

Exercise 2 What is the change in the value of \(f()\) when the input goes from 2 to 4?
Assume \(f(x) \equiv 2 x + 1\)

-4       -2       2       4       9      

question id: drill-M01-5

Exercise 3 What is the rate of change in the value of \(f()\) when the input goes from 2 to 4?
Assume \(f(x) \equiv 2 x + 1\)

-2       -4       2       4       9      

question id: drill-M01-6

Exercise 4 What is the change in the value of \(f()\) when the input goes from 4 to 2?
Assume \(f(x) \equiv 2 x + 1\)

-2       -4       2       4       9      

question id: drill-M01-7

Exercise 5 What is the rate of change in the value of \(f()\) when the input goes from 4 to 2?
Assume \(f(x) \equiv 2 x + 1\)

-2       -4       2       4       9      

question id: drill-M01-8

Exercise 6 What is the rate of change of the function \(f(x) \equiv 3 x - 2\) when the input is 4?

-2       0.3       2       3       10      

question id: drill-M01-9

Exercise 7 What is the change in value of the function \(f(x) \equiv 3 x - 2\) as the input goes from 3 to 3.1?

-2       0.3       2       3       10      

question id: drill-M01-10

Exercise 8 What is the rate of change in value of the function \[f(x) \equiv 3 x - 2\] as the input goes from 3 to 3.1?

-2       0.3       2       3       10      

question id: drill-M01-11

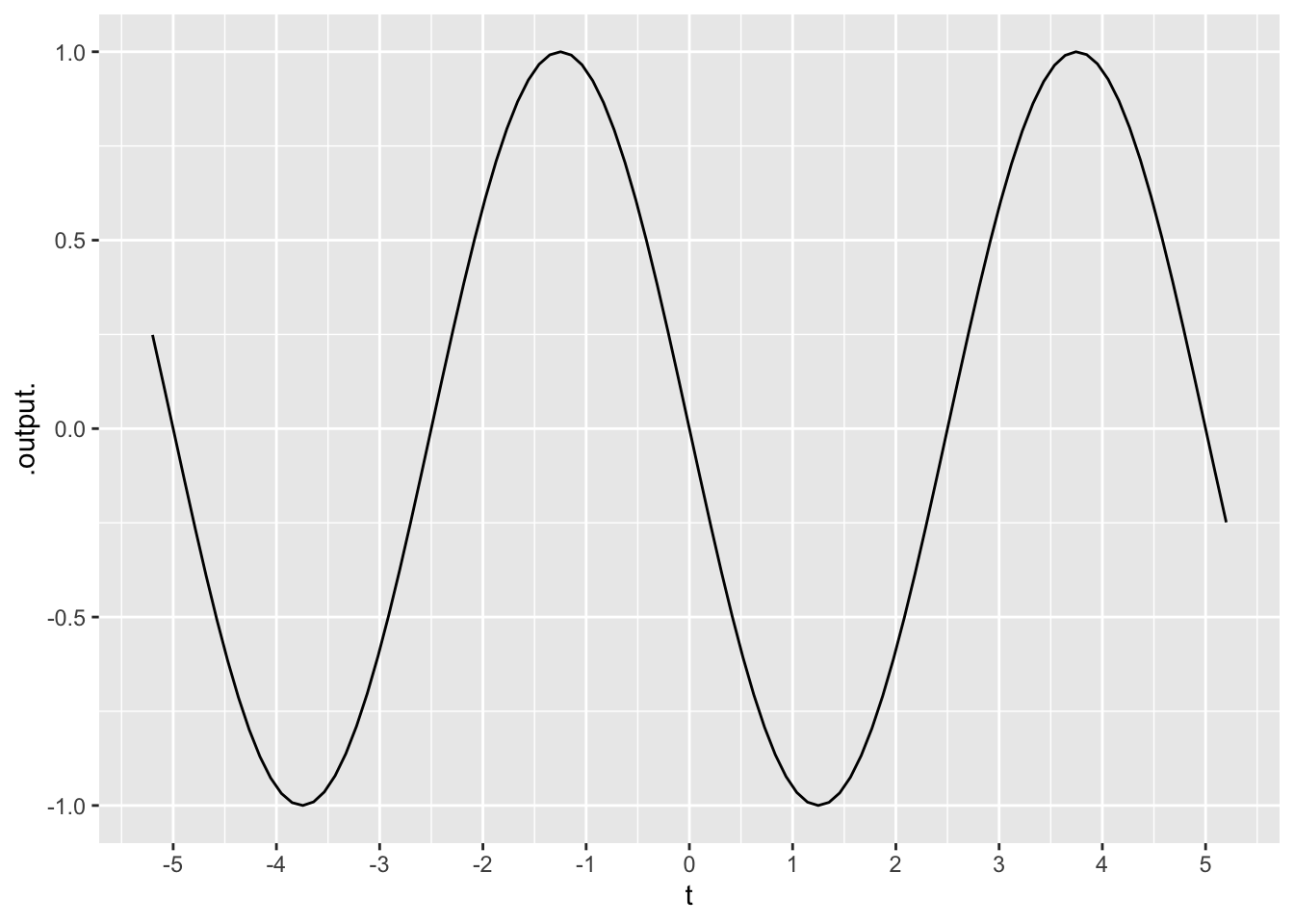
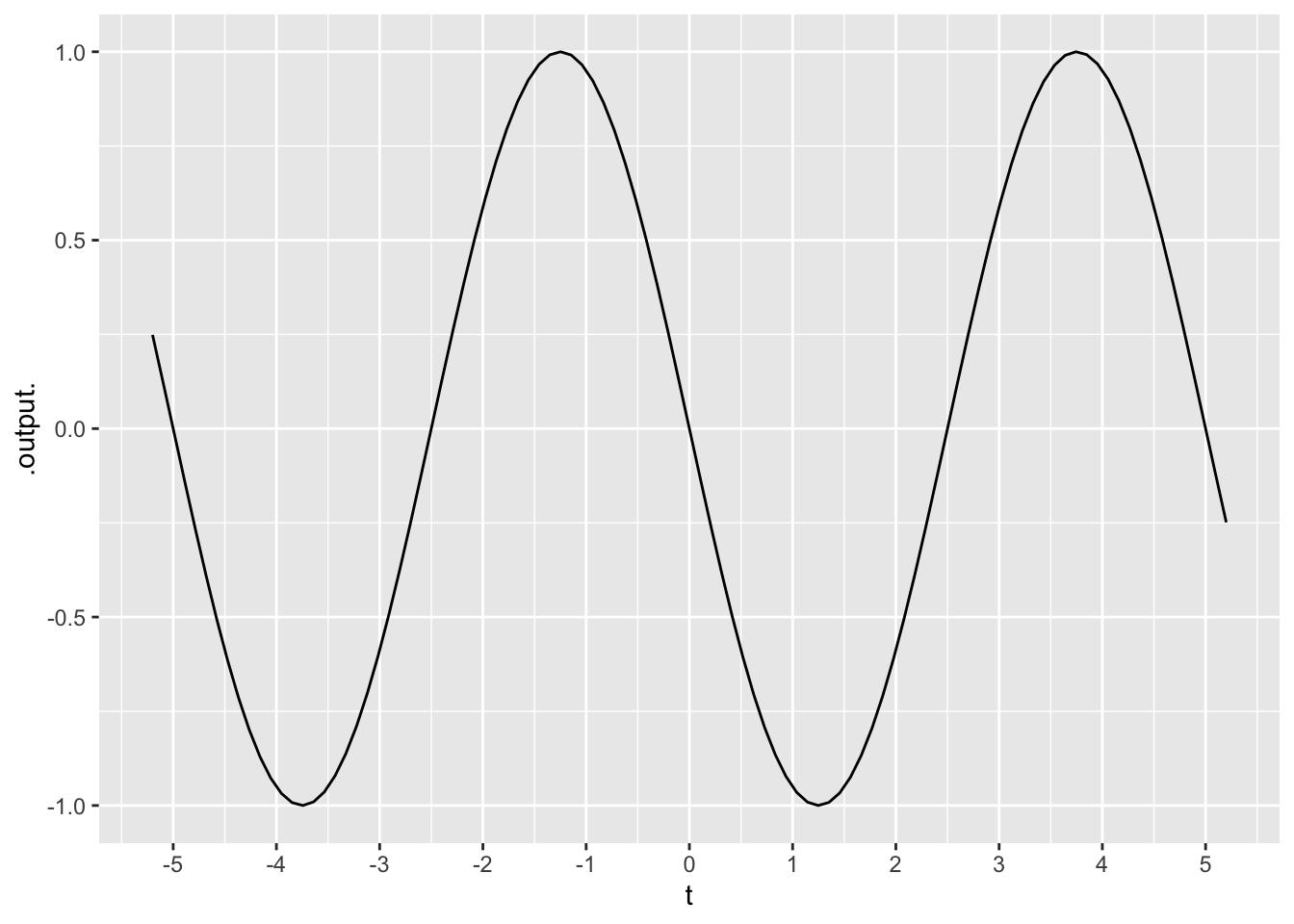
Exercise 9 What is the period of the \(\sin()\) function?

1       \(2/\pi\)       \(\pi/2\)       \(\pi\)       \(2 \pi\)      

question id: drill-M03-2

Exercise 10 Which of these words is most appropriate to describe the function \(g(x) \equiv 2 - 3 x + 4x^3 ?\)

Polynomial       Discontinuous       Periodic       Power-law      

question id: drill-M03-6

Figure 1: .

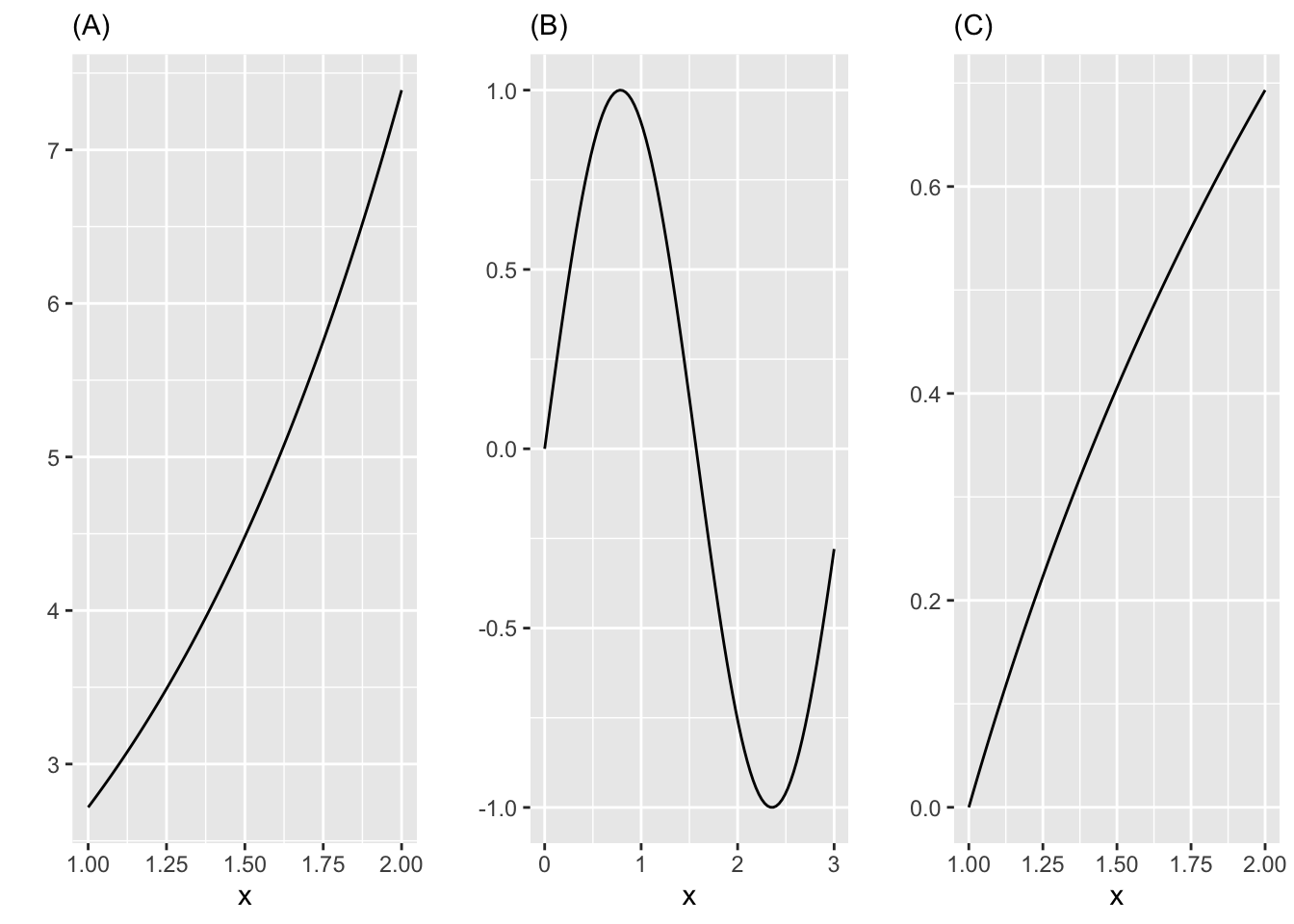
Exercise 11 Which of the functions in Figure 1 is concave up over the domain shown covered by the x-axis?

A       B       C      

question id: drill-M03-12

Figure 2: .

Exercise 12 Which of these functions in Figure 2 has a vertical asymptote?

A       B       C      

question id: drill-M03-13

Figure 3: .

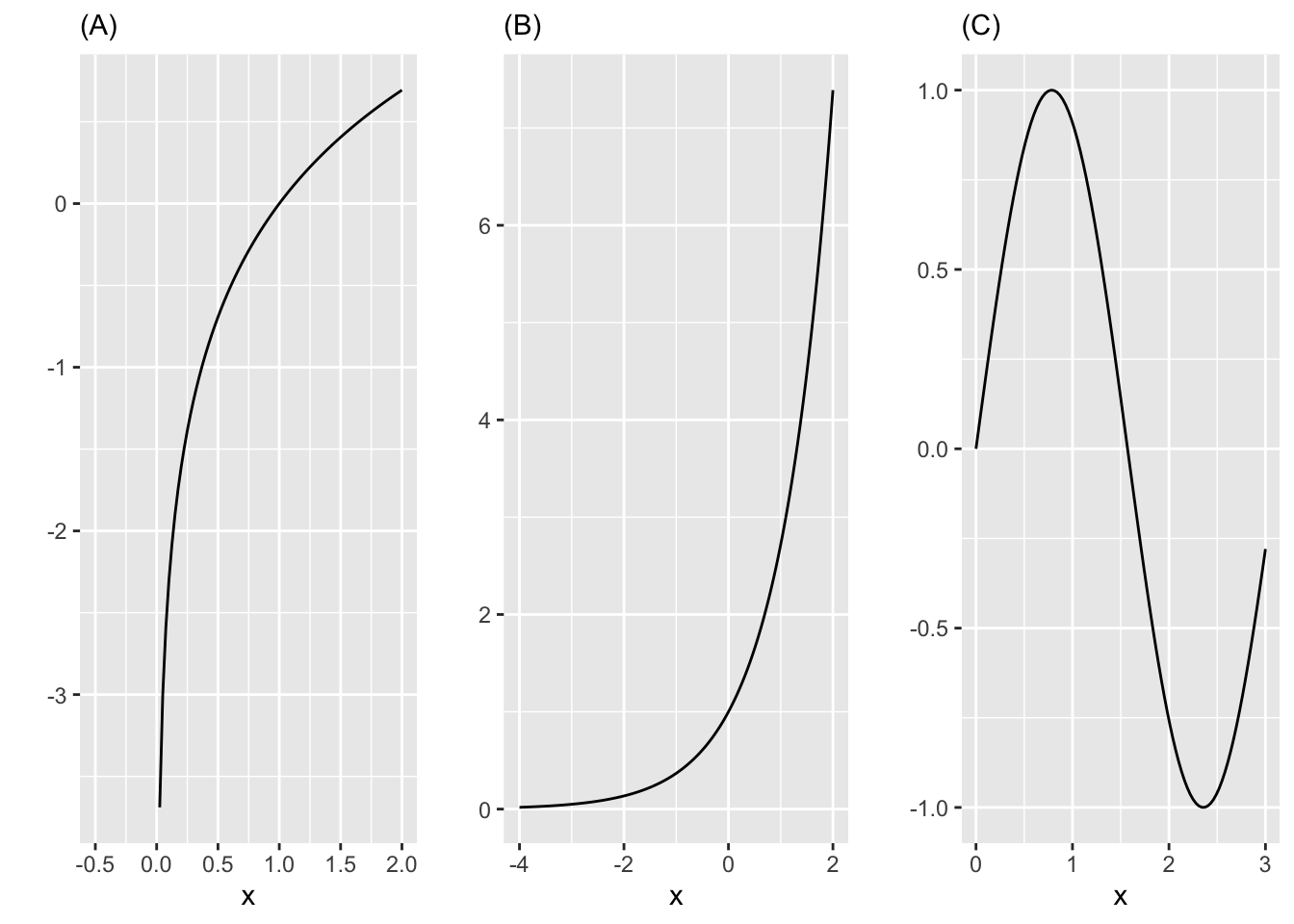
Exercise 13 Which of the functions in Figure 3 has a vertical asymptote?

A       B       C      

question id: drill-M03-14

Figure 4: .

Exercise 14 For the function in Figure 4, where is the horizontal asymptote located?

At \(x=0\)       At \(x=1\)       At 20 as \(x \rightarrow \pm\infty\)      

question id: drill-M03-18

Figure 5: .

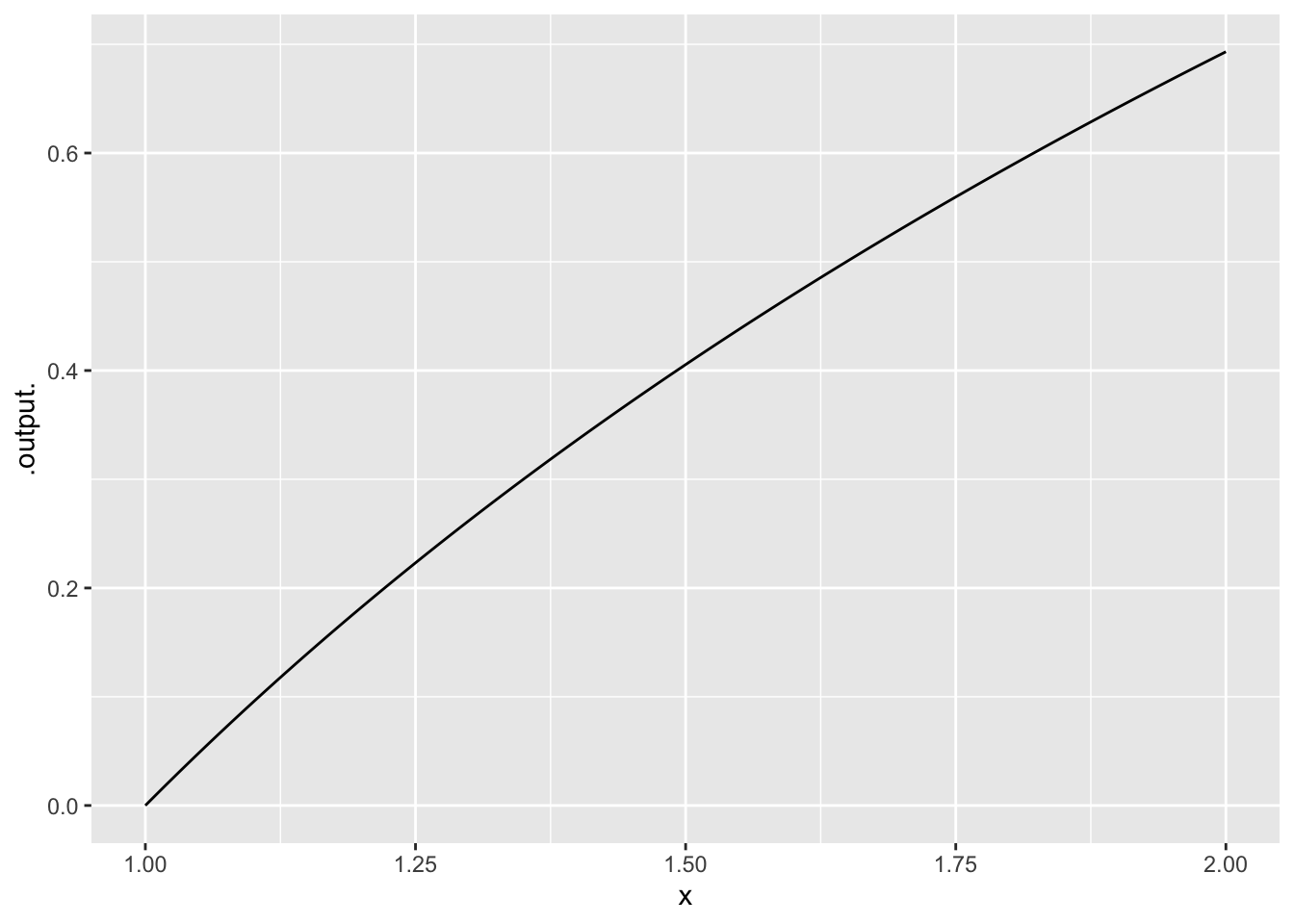
Exercise 15 Does the function in Figure 5 have an inflection point?

yes       no       cannot tell      

question id: drill-M03-16

Figure 6: .

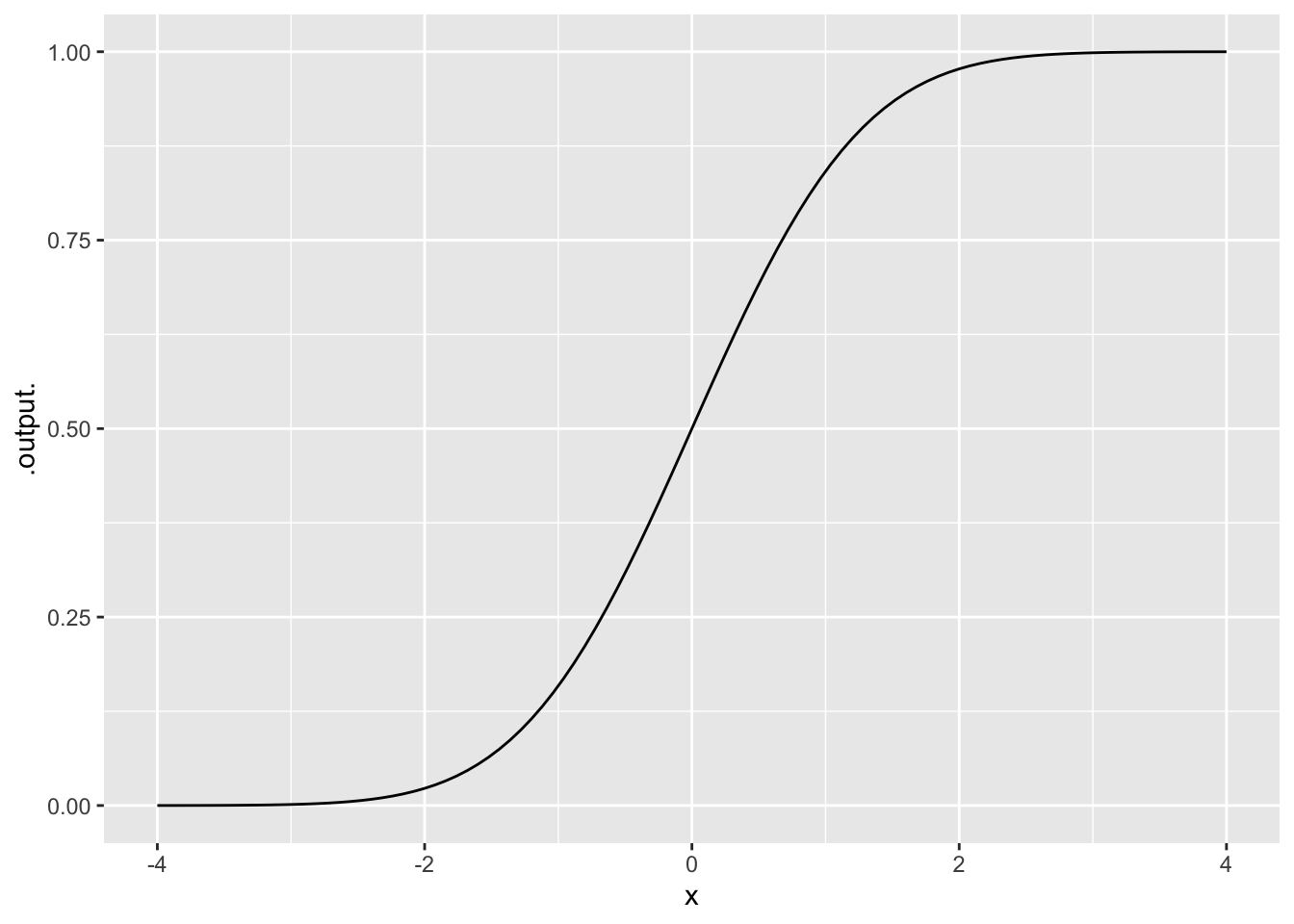
Exercise 16 Does the function in Figure 6 have an inflection point?

yes       no       cannot tell      

question id: drill-M03-17

Figure 7: .

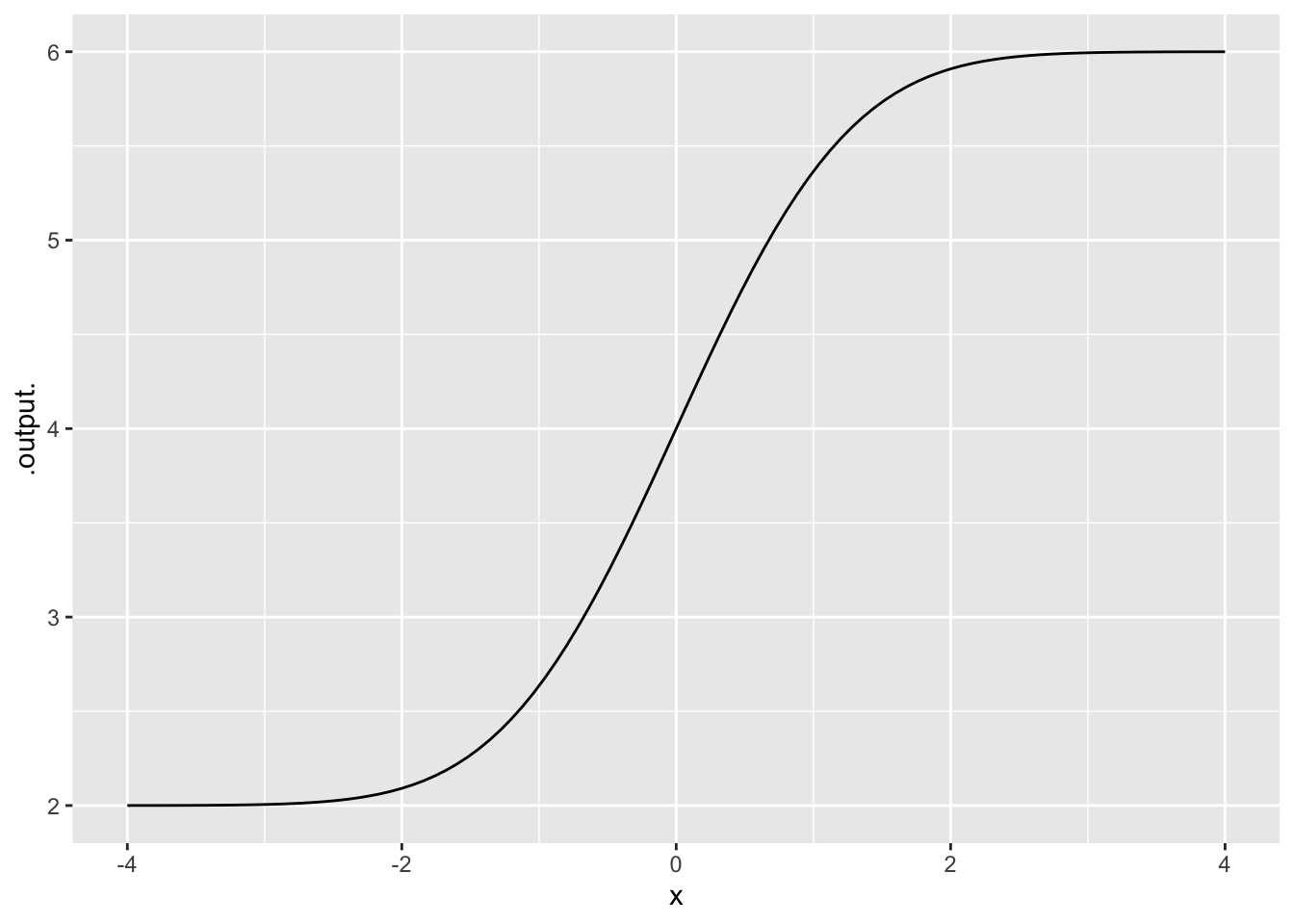
Exercise 17 Which of these is a correct description of a horizontal asymptote in the function in Figure 7?

At 2 as \(x \rightarrow \pm\infty\)

At 2 as \(x \rightarrow -\infty\)

At 6 as \(x \rightarrow -\infty\)

There is no horizontal asymptote.

question id: drill-M03-19

Exercise 18 Which of these is a correct description of a horizontal asymptote in the function in Figure 7?

At 2 as \(x \rightarrow \pm\infty\)

At 2 as \(x \rightarrow \infty\)

At 6 as \(x \rightarrow \infty\)

There is no horizontal asymptote.

question id: drill-M03-20

Figure 8: .

Exercise 19 Which of these is the max of the function in Figure 1?

0       1       2       3       4      

question id: drill-Quiz-2-7

Figure 9: .

Exercise 20 Which of these is an argmin of the function in Figure 9?

\(t = -2.5\)       \(t = -1.25\)       \(t = 0\)       \(t = 1.25\)       \(t = 2.5\)      

question id: drill-Quiz-2-4

Exercise 21 Which of these is an argmax of the function in Figure 9?

\(t = -2.5\)       \(t = -1.25\)       \(t = 0\)       \(t = 1.25\)       \(t = 2.5\)      

question id: drill-Quiz-2-3

Figure 10: .

Exercise 22 According to Figure 10, which of these values is the argmax of the function?

0       1       2       3      

question id: drill-Quiz-1-14

Exercise 23 According to Figure 10, which of these values is the maximum of the function?

0       1       2       3      

question id: drill-Quiz-1-15

Exercise 24 For the function in Figure 10, which of these properties does not apply?

continuous

monotonic

concave-down

no inflection point

question id: drill-Quiz-1-16

Figure 11: .

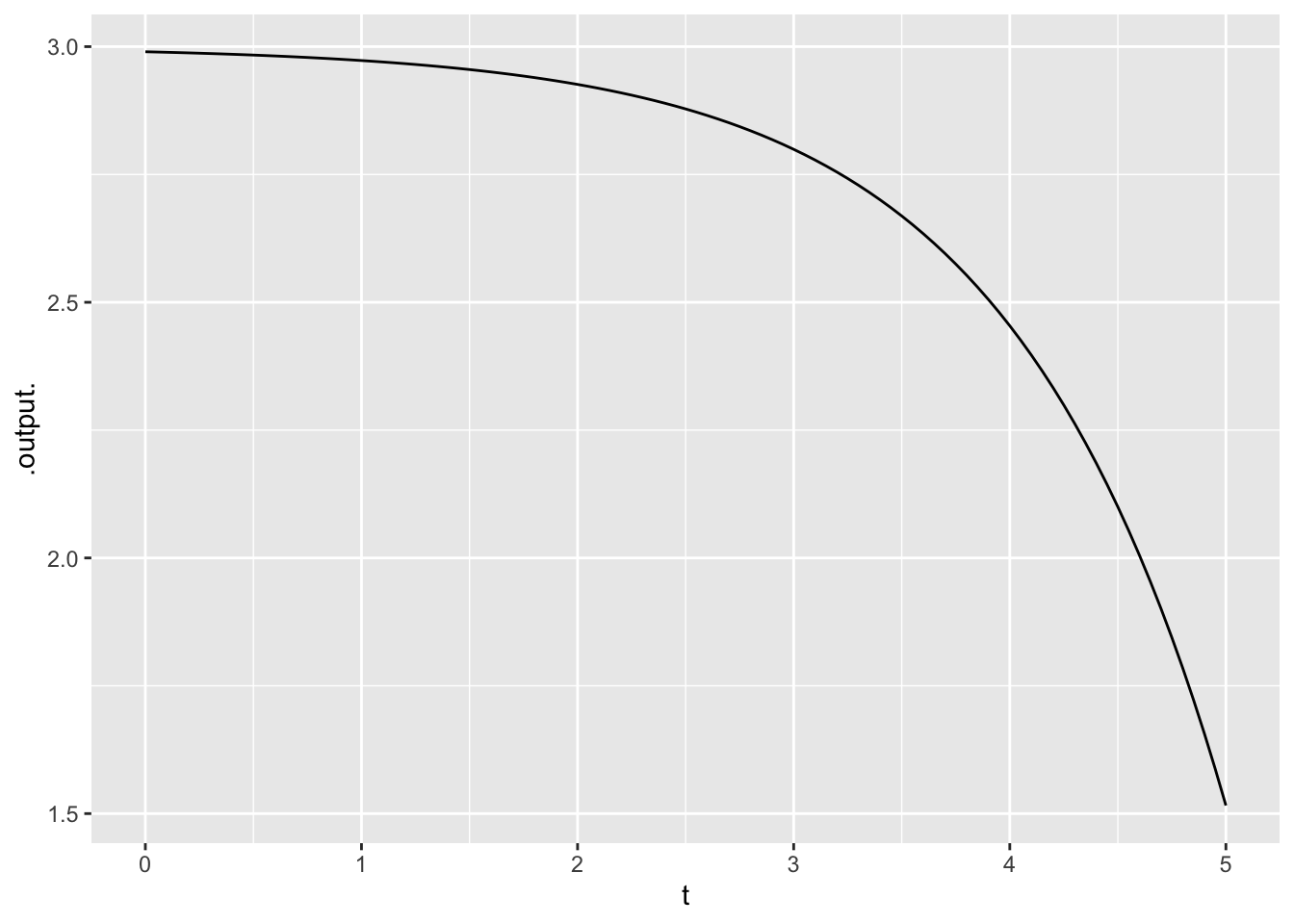
Exercise 25 For the function in Figure 11, which of these properties does not apply?

discontinuous

monotonic

concave-down

no inflection point

question id: drill-Quiz-1-17

Figure 12: A periodic function

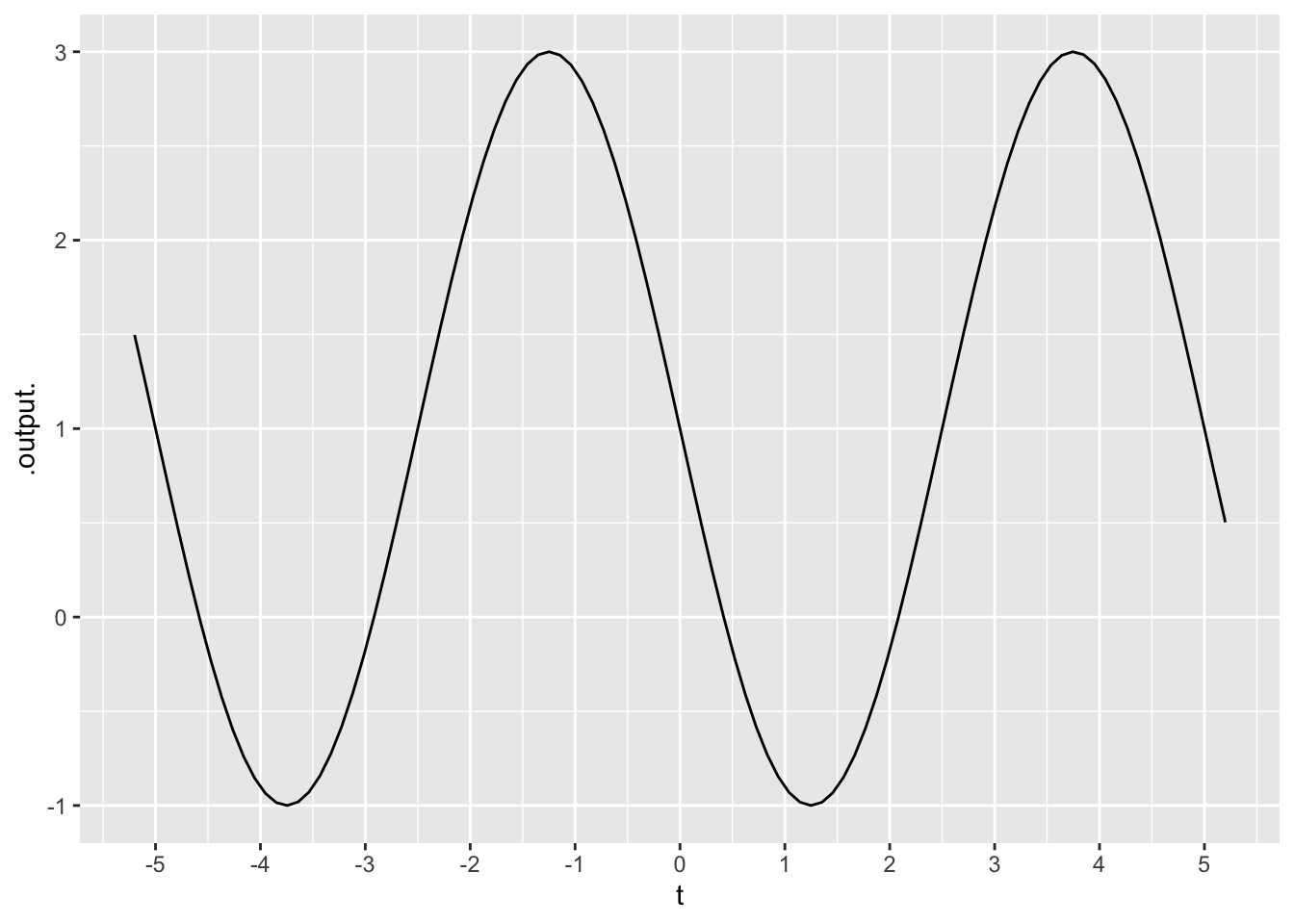
Exercise 26 What’s the period of the function graphed in Figure 12?

1       2       3       4       5      

question id: drill-Quiz-2-22

Exercise 27 Which of these pattern-book functions has a discontinuity?

\(g(x) \equiv x^{-1}\)       \(g(x) \equiv - x^1\)       \(\text{dnorm}(x)\)       \(\sin(x)\)      

question id: drill-M03-1

Exercise 38 For each of the following, plot out the function over an appropriate graphics domain to determine whether the statement is true or false.

Exercise 28 The function \(f(t)\equiv \sin(t)\) has a local max of \(1\) somewhere on the domain \(-\infty < t < \infty\).

True       False      

question id: drill-hlbv-1

Exercise 29 The function \(g(x)\equiv e^x\) has an inflection point on the domain \(-\infty < x < \infty\).

True       False      

question id: drill-hlbv-2

Exercise 30 The function \(g(x)\equiv e^x\) is monotonic on the domain \(-\infty < x < \infty\).

True       False      

question id: drill-hlbv-3

Exercise 31 The function \(g(x)\equiv e^x\) has a vertical asymptote.

True       False      

question id: drill-hlbv-4

Exercise 32 The function \(h(x)\equiv \ln(x)\) has a vertical asymptote.

True       False      

question id: drill-hlbv-5

Exercise 33 The function \(h(x)\equiv \ln(x)\) has a horizontal asymptote.

True       False      

question id: drill-hlbv-6

Exercise 34 The function \(\text{inv}(val)\equiv 1/val\) has a vertical asymptote.

True       False      

question id: drill-hlbv-7

Exercise 35 The function \(\text{inv}(val)\equiv 1/val\) has a horizontal asymptote.

True       False      

question id: drill-hlbv-8

Exercise 36 The function \(f(x)\equiv 1/x\) is monotonically decreasing (i.e., monotonic AND decreasing) on the domain \[0<x<\infty\]. (You need only check in the interval \(0<x\leq 100.\))

True       False      

question id: drill-hlbv-9

Exercise 37 The function \(\text{inv}(val)\equiv 1/val\) is continuous.

True       False      

question id: drill-hlbv-10

Exercise 39  

  1. What is the maximum number of horizontal asymptotes that a function can have?
one       two       three       as many as you like      

question id: seal-wake-bed-1

  1. True or false. A function can cross its horizontal asymptote.
True       False      

question id: seal-wake-bed-2

  1. What is the maximum number of vertical asymptotes that a function can have?
one       two       three       as many as you like      

question id: seal-wake-bed-3

  1. True or false: A function can cross its vertical asymptote.
True       False      

question id: seal-wake-bed-4

No answers yet collected