Chap 47 Exercises

$$$$

Exercise 1 Create a function, which iterated sufficiently from a starting guess, will implement Newton’s method to calculate $\sqrt{10}$.

1. Which of these functions is appropriate to use in Newton’s method for calculating $\sqrt{10}$?

$f(x)\equiv x^2-10$

$f(x)\equiv x-\sqrt{10}$

$f(x)\equiv (x-10{)}^2$

question id: aspen-dig-ship-1

Now you will translate $f(x)$ into a function, when iterated from some starting guess $x_0$, will tend toward a zero of $f(x)$. The function will have the form $$N(x)\equiv x-\frac{f(x)}{f^{\prime }(x)}.$$

2. What is the function $f^{\prime }(x)$ for the $\sqrt{10}$ problem?

$2x-10$

$2x$

$\frac{1}{3}{x}^3+10x+C$

$x$

question id: aspen-dig-ship-2

3. Which of these is the correct form for the Newtons-method iterator $N(x)\equiv x-\frac{f(x)}{f^{\prime }(x)}$?

$N(x)\equiv x-\frac{x^2-10}{2x}$

$N(x)\equiv x+\frac{x^2-10}{2x}$

$N(x)\equiv x+\frac{2x}{x^2-10}$

$N(x)\equiv x-\frac{2x}{x^2-10}$

question id: aspen-dig-ship-3

Implement $N(x)$ in Active R chunk 1.

Active R chunk 1

1

4. Using $N()$ as the dynamics and starting with $x_0=1$, what is $x_5$?

5.5

3.659091

3.141593

3.196005

3.162456

3.162354

3.162278

question id: aspen-dig-ship-4

5. Modify N() to find $\sqrt{20}$. Starting at $x_0=1$, how many times do you have to apply your new N() to get an answer right to within 1% of the true number?

After 2 steps we get 4.202

After 3 steps we get 4.713.

After 3 steps we get 4.472.

After 4 steps we get 4.472.

After 4 steps we get 4.478.

question id: aspen-dig-ship-5

6 Modify your N() once again to find $\sqrt[3]{10}$. (That is, the cube-root of 10.) Starting at $x_0=1$, take 3 Newton steps. What is $x_3$?

2.154

2.320

2.875

2.912

question id: aspen-dig-ship-6

Exercise 2 We introduced Newton’s method as a technique for finding zeros of functions. For instance, for finding zeros of $g(x)$, you would apply the function better() iteratively to an initial guess $x_0$.

$\text{better}(x)\equiv x-\frac{g(x)}{{\partial }_{x}g(x)}$

1. Suppose your goal is not to find a zero of $g(x)$ but instead to find an argmax. One way to do this is to find the zeros of ${\partial }_{x}g(x)$. Write down the Newton-step suitable for the argmax problem.

question id: kid-rise-coat-1

2. Imagine that $g(x)$ has an output of miles-per-gallons and an input speed in miles-per-hour. What will be the dimension of the Newton step for the optimization problem?

question id: kid-rise-coat-2

3. Taking into account the dimension of the input $x$ and of the output $f(x)$, what is the dimension of the step $-f^{\prime }(x_0)/f^{″}(x_0)$. Explain why this makes sense in terms of what a step needs to be.

question id: kid-rise-coat-3

Exercise 3  

1. Which of the following R/mosaic functions takes an initial condition as one of the inputs?

antiD()

D()

Iterate()

question id: birch-wake-linen-1

2. Which of the following R/mosaic functions requires that you specify a domain as one of the inputs to the function?

antiD()

D()

Iterate()

Solve()

question id: birch-wake-linen-2

3. The R/mosaic functions Solve() and argM() return what kind of computer object?

a number

a function

a graph

a data frame

question id: birch-wake-linen-3

Activities

Exercise 4 As an example of situation where Newton’s method fails, consider $x_0$ accidentally picked close to an argmax, that is $f^{\prime }(x_0)\approx 0$. (The situation is illustrated in Figure 1.) The length of the Newton step is proportional to $1/f^{\prime }(x_0)$, which is large when $f^{\prime }(x_0)\approx 0$. Such a Newton step can produce $x^{\star }$ further from the actual solution rather than closer to it.

Figure 1: An unlucky choice of $x_0$ (marked in magenta) near a local maximum has resulted in a Newton step that is too long. The Newton step creates $x_1\approx -3$, far to the left of the actual zero crossing which is near $x\approx 0$.

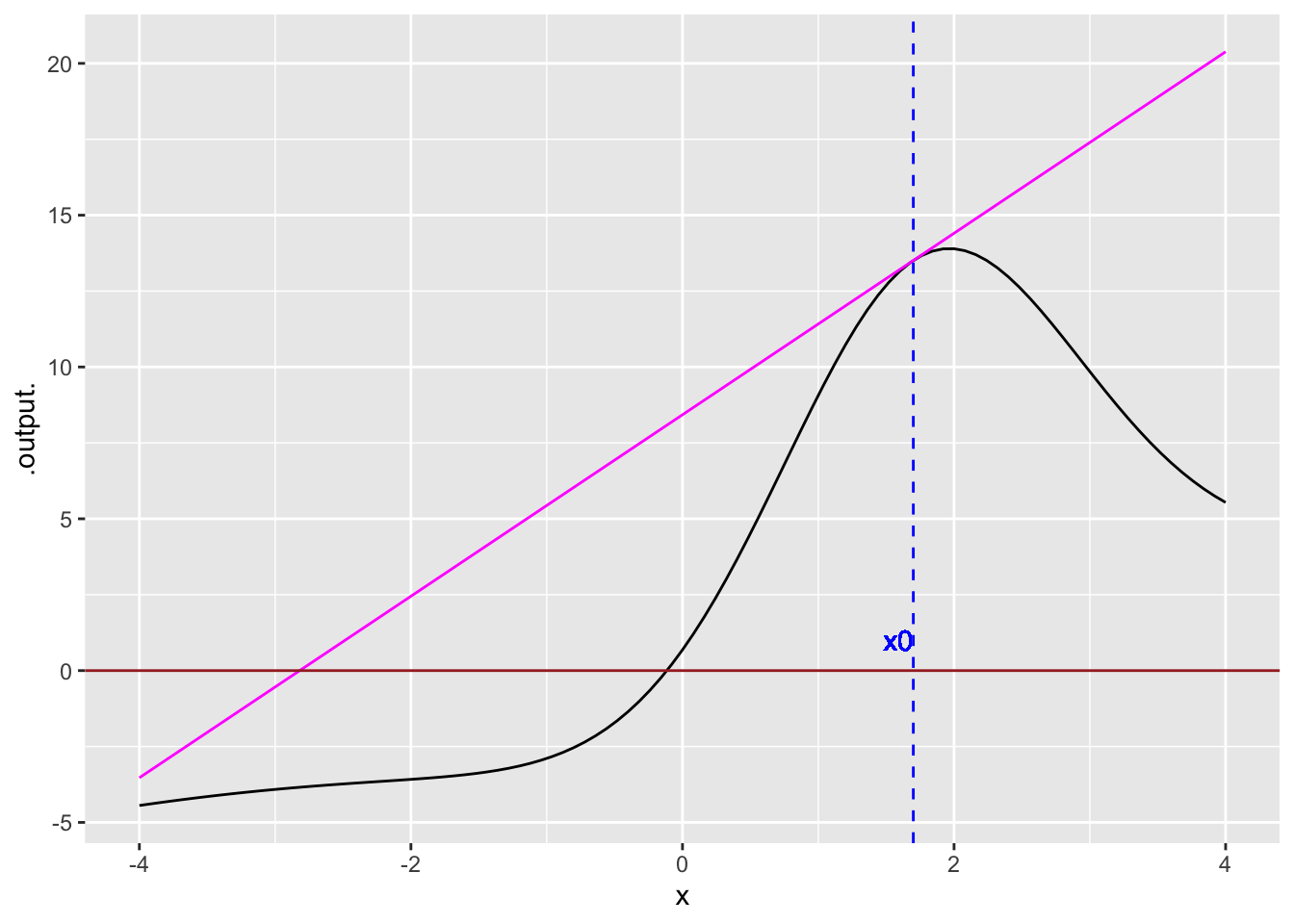
1. Take a second Newton step, that is, a step starting at $x_1$ and ending at $x_2$. You can eyeball the linear function that approximates $f(x)$ near $x_1$. What is the approximate value of $x_2$.

2. Try a simple modification to Newton’s method that can help deal with such situations. In the figure above, the full Newton step puts $x_1$ where the dotted line crosses the brown line. This full step has length $\parallel x_1-x_0\parallel$, in this case roughly 4.5.

In your modification, instead of taking the full Newton step, take a step from $x_0$ that is only half as long. That half step will bring you to a new $x_1$. From there, take another half Newton step to find $x_2$. Will this process converge toward the actual zero crossing of $f(x)$?

Exercise 5  

1. Write a Newton-step better() function to solve for $x$ in the equation $\sin (x)=\cos (x)$. Start with the guess $x_0=0$ and iterate better() enough times to get $\parallel x_i-x^{\star }\parallel <0.001$.

To help, we will give the hint that $x^{\star }\approx 0.785$.

Active R chunk 2

1

2. Suppose we hadn’t told you the answer $x^{\star }$. How could you know, just from your iterations of better(), that you are very close to the true answer.

question id: fish-ring-door

Exercise 6 A simple robot arm to move things in the $(x,y)$ plane consists of two links, the first connected to the base of the robot and the second to the free end of the first link, as in the diagram. At the end of the second link is a tool, such as a drill. Such a robot would be used to drill a series of precisely positioned whole in a metal plate.

Each link is moved by a digitally-controlled motor. To position the robot, commands are sent to the two motors to set their respective angles. For instance, in the diagram the motor-1 angle, ${\theta }_1$ is set to 45 degrees, while the motor-2 angle ${\theta }_2$ is set to -60 degrees.

The problem faced by the robot designer is to allow the user to input a series of $(x,y)$ coordinates (where the holes are to be drilled) and have the robot controller calculate the resulting angles.

For simplicity, assume that the link lengths are both $L=1$, but generalizing this to two different link lengths would not be difficult.

At this point, play with the problem a bit. Mark a point on your desk or paper. This will be the location of the base of the robot. Take two pencils, let’s call them “yellow” and “green,” putting the eraser of yellow at the base location and the eraser of green at the tip of yellow. Now, pick another point on your desk or paper to be the target for the robot arm. (This must be closer to the base than the sum of lengths of the two pencils.) Change the orientation of the pencils, keeping yellow attached to the base and green attached to the tip of yellow. Your job is to find an orientation that will place the tip of green on the target. Try different target points until you feel comfortable that you understand how to solve the problem.

Now to create a mathematical model of the situation so that we can automate the solution. The purpose of this model is to find ${\theta }_1$ and ${\theta }_2$ given the $(x,y)$ position of the target.

From your experience using pencils as the model of the robot, you may have noticed that the location of the “elbow” of the robot arm is key to the solution. Find the right position for the elbow and the angles can be calculated from trigonometry.

Note that the position of the elbow, which we will denote with coordinates $(u,v)$ is determined solely by $L$ and ${\theta }_1$.

1. Write down a formula for the $u$ and for the $v$ position of the elbow as a function of ${\theta }_1$ (taking the base as the origin). Hint: sine and cosine functions are relevant.

question id: snake-get-ring-1

2. Using Active R chunk 3, implement the formulas from (1) into two functions, one called elbow_u(theta1) and the other elbow_v(theta1).

Active R chunk 3

1

3. Using Active R chunk 4, write another function, elbow_to_target_dist(theta1, x, y) that will use elbow_u() and elbow_v() to calculate the distance from the elbow to the target point $(x,y)$. (The distance will be $\sqrt{(x-u{)}^2+(y-v{)}^2}$.)

Active R chunk 4

1

4. In Active R chunk 5, write yet another function, dist_at_theta(theta1, x, y) that, given an angle theta, will return the distance from the elbow to the target. The logic is to use elbow_u() and elbow_v() to find the location of the elbow $u$ and $v$ and then give these as the argments to elbow_to_target_dist().

Active R chunk 5

1

5. The next phase of the solution is to use elbow_to_target_dist(theta1, x, y) to find a value of theta1 that will make the distance equal to the length $L$ of link2. When you have found this theta1, you will know the position of the elbow that is consistent with reaching the target from the base with the two links.
   1. Pick a target location. This can be anything within distance $2L$ from the base. We will call the coordinates of your target target_x and target_y.
   2. Plot out elbow_to_target_dist(theta1, x=target_x, y=target_y) as a function of theta1 over the domain $-\pi \le {\theta }_1\le \pi$.
   3. Locate a value of ${\theta }_1$ where the output of the function is $L$.

Active R chunk 6

1

6. Write another function, elbow_theta1(x, y) that takes the $(x,y)$ position as input and produces as output suitable value(s) of ${\theta }_1$. To do this within the elbow_theta1(x, y) function, use Zeros(dist_at_theta(theta1) - L, bounds(theta1=-pi:pi)).

Active R chunk 7

1

Answer

47-exercises.rmarkdown

No answers yet collected