6  Describing functions

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Reading questions

Reading question 6.1 Which of these is not a function-shape concept discussed in Chapter 6?

periodicity       concavity       curl       monotonicity      

question id: 6-words

Reading question 6.2 Draw a graph of a periodic function of your own construction. Use your imagination. (Bring your drawing to class, either as a phone/picture or as a piece of paper.)

For grading purposes, once you have made your drawing, copy the following into the text box:

I have honorably completed the periodic-function drawing task.

question id: draw-period

Reading question 6.3 Which of these pattern-book functions are monotonic?

reciprocal       square       sigmoid       gaussian      

question id: monotonic-fun

Reading question 6.4 Which of these pattern-book functions is not monotonic and decreasing over part of their domain?

gaussian       logarithm       reciprocal       square       sinusoid      

question id: monotonic2

Reading question 6.5 Does the exponential function have a local maximum?

yes       no      

question id: exp-max

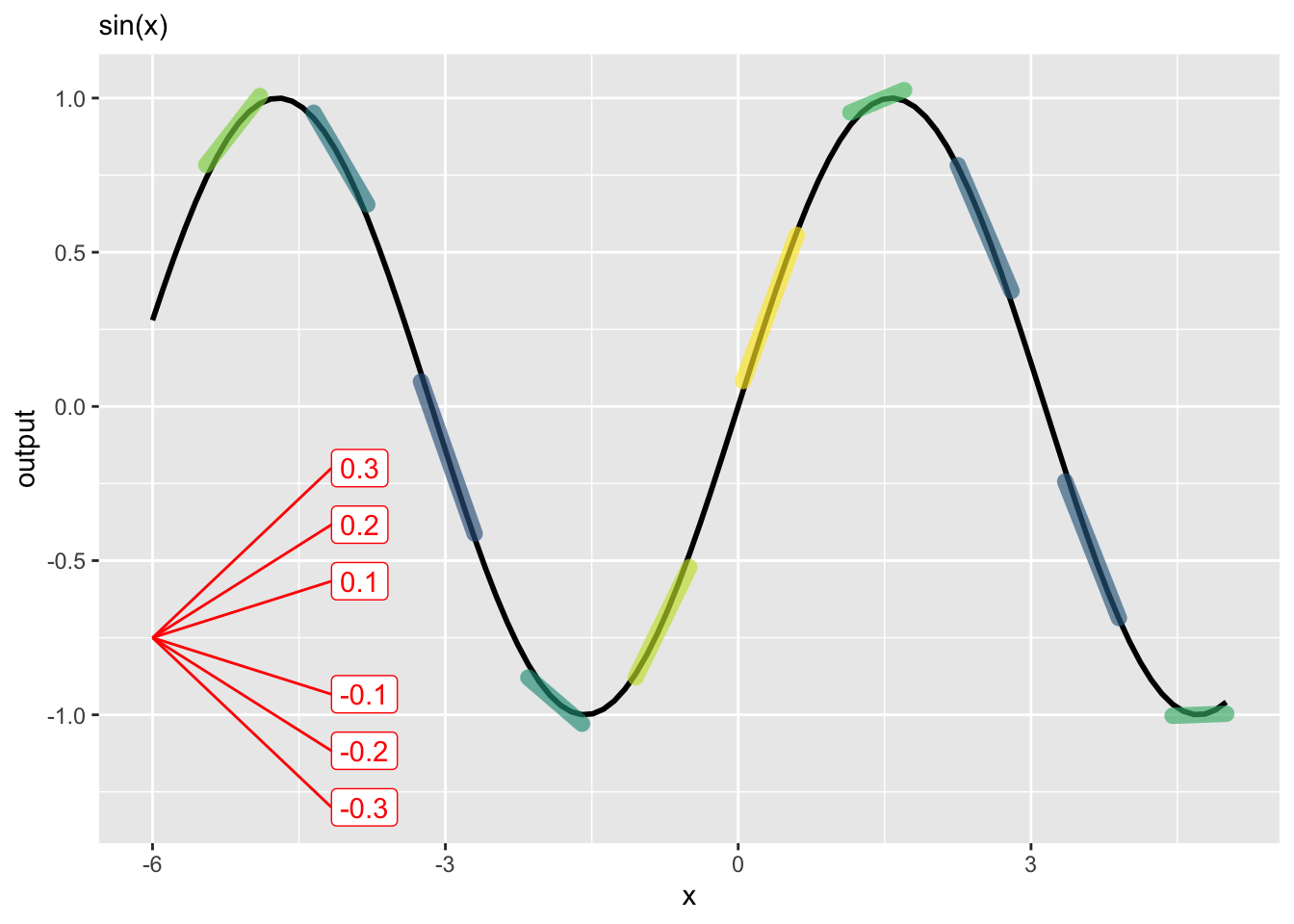
Reading question 6.6 These questions refer to Figure 6.2 in the Reading.

  1. At which value of \(x\) does the function have a negative slope?
-5       -3       0       4      

question id: sin-slope-a

  1. The red annotations in Figure 6.2 indicate the numerical value of lines drawn at the indicated slope. Which of these values of \(x\) is closest to an input value where the function has a slope of about 0.3?
-4.5       -0.2       1.7       4.0      

question id: sin-slope-b

  1. Again referring to the red annotations in Figure 6.2 … The line labelled 0.3 seems to be at about 45 degrees to the horizontal. This corresponds to a slope value of 1. Yet the line is marked as having a slope of 0.3, an apparent paradox. Give an explanation that accounts for the paradox.
No answers yet collected