Chap 13 Exercises

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1  

  1. What is the exact input to the pattern-book logarithm function where the output is 0?
0       0.3989423       1/2       1      

question id: nac89-1

  1. What is the exact input to the pattern-book reciprocal function where the output is 1?
0       0.3989423       1/2       1      

question id: nac89-2

  1. What is the exact input to the pattern-book identity function where the output is 1/2?
0       0.3989423       1/2       1      

question id: nac89-3

  1. The pattern-book square function just touches the horizontal axis. What’s the input where this happens?
0       0.3989423       1/2       1      

question id: nac89-4

Exercise 2 The graphs of functions and their inverses are related by a flip around the line of identity, shown in green Figure fig-inverse-flip-both.

Figure 1: The black curve is the graph of \(e^x\), \(\color{magenta}{\text{magenta}}\) shows \(\ln(x)\).
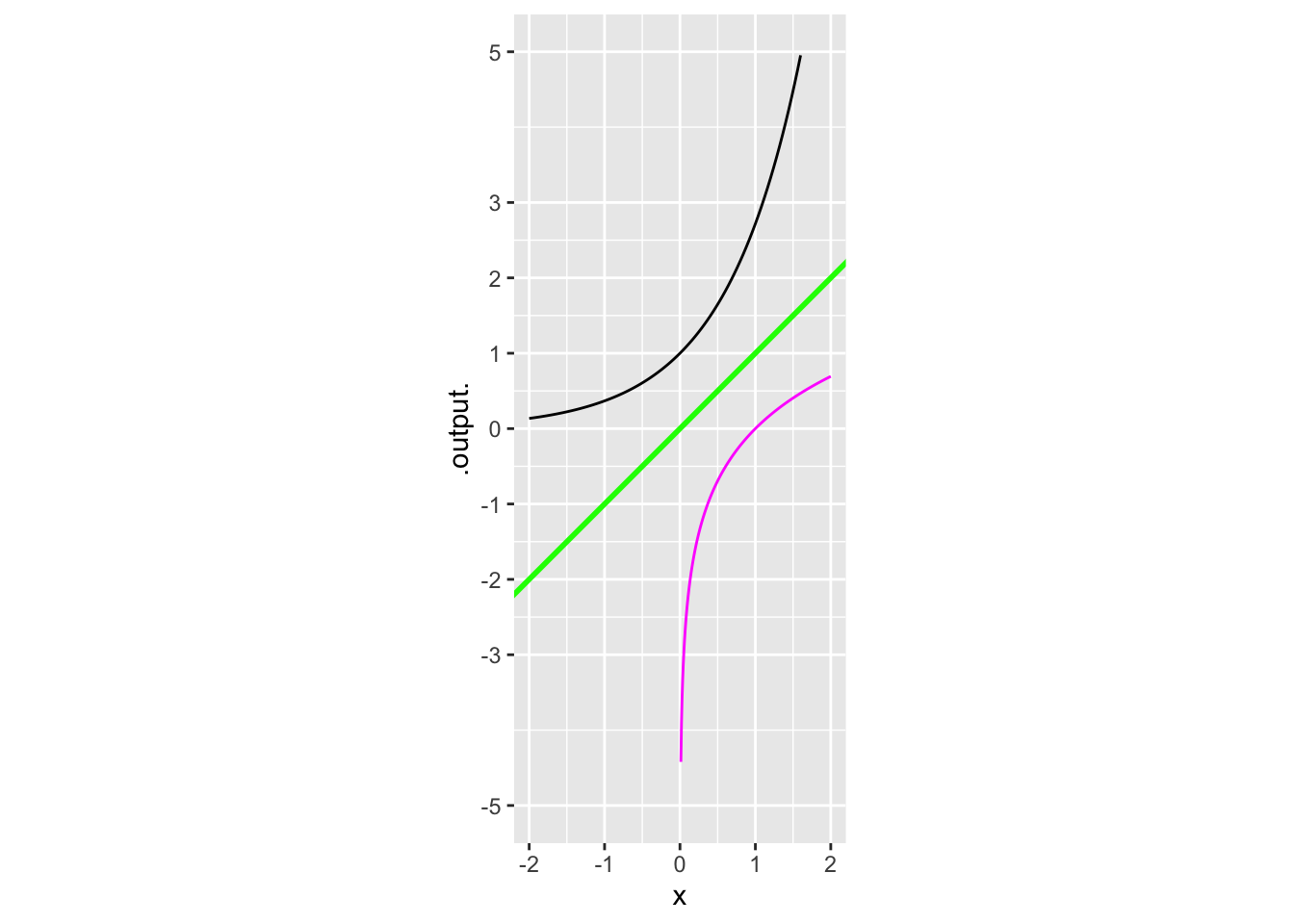
  1. Is the magenta curve the graph of a function? (Hint: Does it pass the vertical line test?)
Yes       No      

question id: inverse-flip-one-1a

  1. Which of these functions is graphed in magenta?
\(1/x\)       \(\ln(x)\)       \(\sqrt{x}\)       \(e^{-x}\)       \(-e^{x}\)      

question id: inverse-flip-one-1b

Exercise 3 Consider the function random function \(h(x)\) graphed by the code in this interactive R chunk:

You will run the plotting command several times to zoom in on each of the five crossings at level \(b\) listed below.

For each of the values \(b\) listed below, use graphical zero finding to identify one or more \(x^\star\) that will satisfy \(h(x^\star) = b\). (Your answer should be precise to \(\pm 0.1\).)

  1. \(b=100\)
  2. \(b=300\)
  3. \(b=500\)
  4. \(b= -100\)

question id: snail-pitch-knife-essay

Exercise 4  

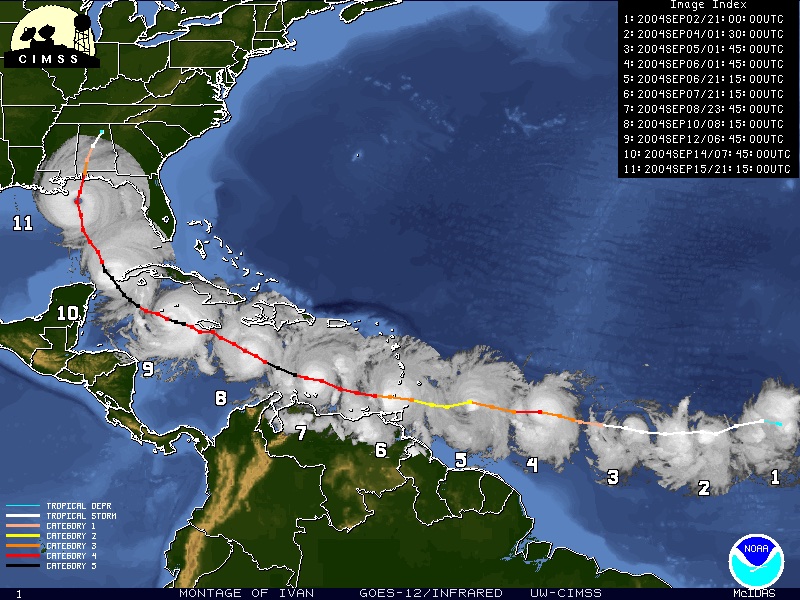
Figure 2: The path of Hurricane Ivan in 2004 as it moved over Jamaica to Alabama to Virginia to Florida to Texas.

Consider only days 2 through 11 in answering the following questions. (Recall that longitude is along the horizontal axis, while latitude is along the vertical.)

  1. For the path in Figure fig-hurricane-ivan, is the latitude a function of the longitude?
Yes.       No.      

question id: hurricane-ivan-1

  1. Is the longitude a function of the latitude?
Yes.       No.      

question id: hurricane-ivan-2

Exercise 5 Consider the problem of finding a value of \(x\) such that \(cos(x) = x^2\). This is easy to do graphically: find the input where the graphs of \(cos(x)\) and \(x^2\) cross.

Using the interactive chunk below, create a function \(h(x)\) that is zero when the equation is satisfied. Pass the tilde expression h(x) ~ x to the R/mosaic Zeros() operator to find a precise numerical answer to the problem:

Exercise 6 Consider finding the argmin and argmax of a straight-line function such as \(g(x) \equiv 4x - 1\). We’ll use the argM() function.

Note that a straight-line function has no local min or maximum. Yet argM() produced a result.

Experiment by changing the parameters on the linear function and the domain over which the operation is performed. Explain what simple strategy argM() uses to give a result even when the function has no local min nor max.

question id: duck-swims-pond

No answers yet collected