Chap 30 Exercises

$$$$

Loading webR...

Exercise 1 Here is a direction, $\overrightarrow{\mathbf{D}}$:

$$\overrightarrow{\mathbf{D}}\equiv \left(\begin{array}{c}2\\ 5\end{array}\right)$$ Find the projection of $\overrightarrow{\mathbf{V}}\equiv (1,3{)}^T$ onto $\overrightarrow{\mathbf{D}}$.

$0.59\overrightarrow{\mathbf{D}}$

${(5,6)}^T$

$\overrightarrow{\mathbf{V}}-{(5,6)}^T$

question id: kangaroo-light-bowl-1

Find the residual vector $\overrightarrow{\mathbf{R}}$ from the projection of $\overrightarrow{\mathbf{V}}\equiv (1,3{)}^T$ onto $\overrightarrow{\mathbf{D}}$.

$\overrightarrow{\mathbf{R}}=(0.83,2.07)$

$\overrightarrow{\mathbf{R}}=(0.31,1.28)$

$\overrightarrow{\mathbf{R}}={(1.28,0.31)}^T$

$\overrightarrow{\mathbf{R}}=(0.83,0.31)$

question id: kangaroo-light-bowl-2

Find the projection of $\overrightarrow{\mathbf{V}}\equiv (3,1{)}^T$ onto $\overrightarrow{\mathbf{D}}$.

$0.379\overrightarrow{\mathbf{D}}$

${(5,6)}^T$

$\overrightarrow{\mathbf{V}}-{(5,6)}^T$

question id: kangaroo-light-bowl-3

Find the residual vector $\overrightarrow{\mathbf{R}}$ from the projection of $\overrightarrow{\mathbf{V}}\equiv (3,1{)}^T$ onto $\overrightarrow{\mathbf{D}}$.

$\overrightarrow{\mathbf{R}}={(-0.17,0.07)}^T$

$\overrightarrow{\mathbf{R}}=(-0.17,0.07)$

$\overrightarrow{\mathbf{R}}={(0.07,-0.17)}^T$

$\overrightarrow{\mathbf{R}}=(0.07,-0.17)$

question id: kangaroo-light-bowl-4

Exercise 2 The text gives a formula for the scalar multiplier $\alpha$ such that $\alpha \overrightarrow{a}=\text{modeledby}\overrightarrow{b}\overrightarrow{a}$:

$$\alpha =\frac{\overrightarrow{b}\bullet \overrightarrow{a}}{\overrightarrow{a}\bullet \overrightarrow{a}}.$$ For a <- rbind(5, -2, 3, 7) calculate the scalar multiplier $\alpha$ for each of these $\overrightarrow{b}$ vectors. (Answers have been rounded to 3 decimal places.)

1. b1 <- rbind(1, 0, 0, 0)

-0.057       -0.287       -0.023       0.023       0.287
      0.057      

question id: child-dig-shoe-1

2. b2 <- rbind(0, 1, 0, 0)

-0.057       -0.287       -0.023       0.023       0.287
      0.057
     

question id: child-dig-shoe-2

3. b3 <- rbind(0, 1, 2, 3)

-0.057       -0.287       -0.023       0.023       0.287       0.057
     

question id: child-dig-shoe-3

4. b4 <- rbind(-4, 1, 2, 3)

-0.057       -0.287       -0.023       0.023       0.287
      0.057      

question id: child-dig-shoe-4

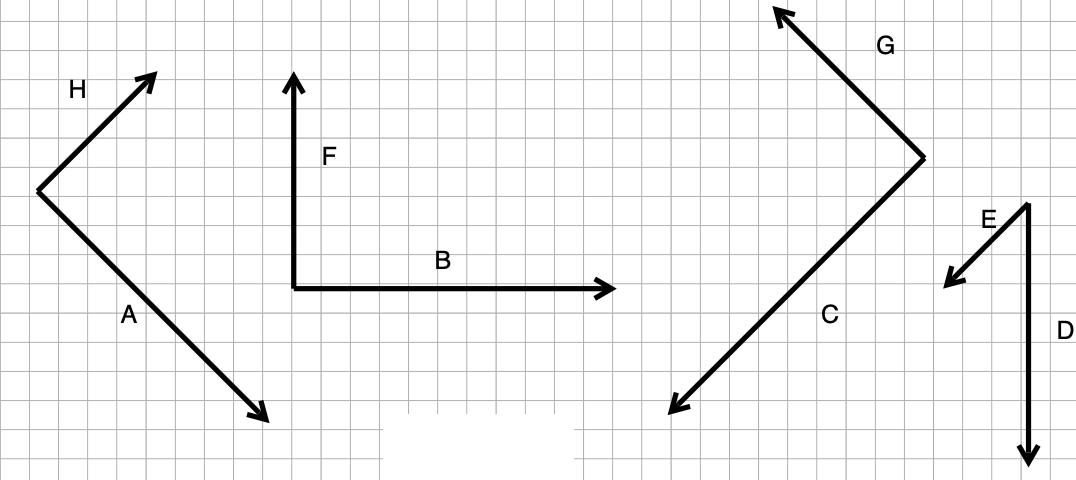
Exercise 3 Here are twelve labeled vectors, A through M. There is a thirteenth vector, labeled “Null vector,” that is a vector of length zero, so it cannot be drawn as an arrow. Note that the direction of the null vector does not matter since the vector length is zero.

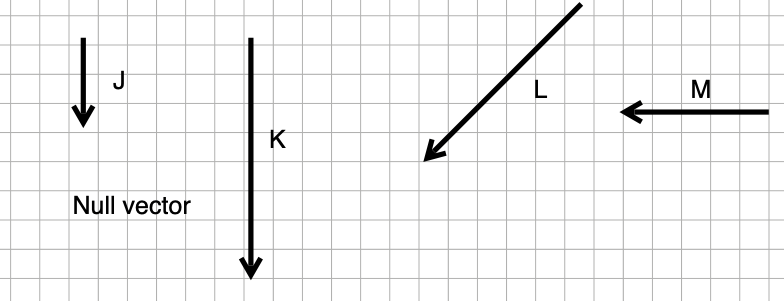
Each of the following statements is of the form, “$\overrightarrow{v}$ projected onto $\overrightarrow{u}$ gives $\overrightarrow{w}$. Say whether the statement is true or false.

1. $\overrightarrow{A}$ projected onto $\overrightarrow{D}$ gives $\overrightarrow{K}$

True

False

question id: beech-build-shirt-1

2. $\overrightarrow{D}$ projected onto $\overrightarrow{E}$ gives $\overrightarrow{L}$

True

False

question id: beech-build-shirt-2

3. $\overrightarrow{J}$ projected onto $\overrightarrow{E}$ gives the null vector.

True

False

question id: beech-build-shirt-3

4. $\overrightarrow{H}$ projected onto $\overrightarrow{A}$ gives the null vector

True       False      

question id: beech-build-shirt-4

5. $\overrightarrow{J}$ projected onto $\overrightarrow{K}$ gives $\overrightarrow{D}$

True       False      

question id: beech-build-shirt-5

6. $\overrightarrow{C}$ projected onto $\overrightarrow{D}$ gives $\overrightarrow{L}$

True       False      

question id: beech-build-shirt-6

7. $\overrightarrow{L}$ projected onto $\overrightarrow{B}$ gives the null vector

True       False      

question id: beech-build-shirt-7

8. $\overrightarrow{E}$ projected onto $\overrightarrow{C}$ gives $\overrightarrow{E}$

True       False      

question id: beech-build-shirt-8

9. $\overrightarrow{G}$ projected onto $\overrightarrow{C}$ gives the null vector.

True       False      

question id: beech-build-shirt-9

10. $\overrightarrow{E}$ projected onto $\overrightarrow{D}$ gives $\overrightarrow{J}$

True       False      

question id: beech-build-shirt-10

11. $\overrightarrow{A}$ projected onto $\overrightarrow{B}$ gives $\overrightarrow{K}$

True       False      

question id: beech-build-shirt-11

12. $\overrightarrow{H}$ projected onto $\overrightarrow{A}$ gives the null vector

True       False      

question id: beech-build-shirt-12

13. $\overrightarrow{F}$ projected onto $\overrightarrow{C}$ gives $\overrightarrow{H}$

True       False      

question id: beech-build-shirt-13

14. $\overrightarrow{C}$ projected onto $\overrightarrow{E}$ gives $\overrightarrow{E}$

True       False      

question id: beech-build-shirt-14

15. $\overrightarrow{E}$ projected onto $\overrightarrow{G}$ gives the null vector

True       False      

question id: beech-build-shirt-15

16. $\overrightarrow{G}$ projected onto $\overrightarrow{B}$ gives $\overrightarrow{C}$

True       False      

question id: beech-build-shirt-16

Exercise 4 Vectors $\overrightarrow{A},\overrightarrow{B},\cdots ,\overrightarrow{H}$ have are defined as A, B, …, H in ?lst-puppy-dream-spoon you can use them in the sandbox. (To see one of these vectors, give a command in the sandbox consisting of just the vector name.)

1

2

3

4

5

6

7

8

A <- rbind(2.1,  -3.4)

B <- rbind(0.3, 4.2)

C <- rbind(-2, 3.8)

D <- rbind(1.1,  -3,  2.2,  -1)

E <- rbind(6,  4,  -2,  -1)

F <- rbind(0,  3,  2,  1)

G <- rbind(1, -2,  1,  1)

H <- rbind(-2, 0, 3, 4)

Active R chunk 1 has commands of the sort used in solving the target problem.

Active R chunk 1

1

2

3

4

5

6

M <- cbind(A, B)    # Problem setup: Matrix packaging up vectors

b <- C              # Problem setup: Target vector 

x <- qr.solve(M, b) # Solve the target problem M %*% x = b for x

bhat <- M %*% x     # Result: projected  vector

resid <- b  - bhat  # Result: residual vector

t(A)  %*%  A        # square length of a vector

Use such commands to answer the following questions.

1. Solve $(\overrightarrow{A},\overrightarrow{C})\cdot \overrightarrow{x}=\overrightarrow{B}$ for $\overrightarrow{x}$. What is the length of $\overrightarrow{x}$?

Exactly 0

About 1.6

About 2.5

About 3.43

About 12

Can’t be solved

question id: puppy-dream-spoon-1

2. Solve $(\overrightarrow{A})\cdot \overrightarrow{x}=\overrightarrow{B}$ for $\overrightarrow{x}$. What’s the length of the residual?

Exactly 0

About 0.3

About 1.6

About 2.5

About 3.43

About 12

Can’t be solved

question id: puppy-dream-spoon-2

3. Solve $(\overrightarrow{D},\overrightarrow{E})\cdot \overrightarrow{x}=\overrightarrow{F}$ for $\overrightarrow{x}$. What is the length of the residual?

Exactly 0

About 0.3

About 1.6

About 2.5

About 3.43

About 12

Can’t be solved

question id: puppy-dream-spoon-3

4. Solve $(\overrightarrow{D},\overrightarrow{E},\overrightarrow{F})\cdot \overrightarrow{x}=\overrightarrow{G}$ for $\overrightarrow{x}$. What is the length of the residual?

Exactly 0

About 0.3

About 1.6

About 2.5

About 3.43

About 12

Can’t be solved

question id: puppy-dream-spoon-4

5. Solve $(\overrightarrow{D},\overrightarrow{E},\overrightarrow{F},\overrightarrow{G})\cdot \overrightarrow{x}=\overrightarrow{H}$ for $\overrightarrow{x}$. What is the length of the residual?

Exactly 0

About 0.3

About 1.6

About 2.5

About 3.43

About 12

Can’t be solved

question id: puppy-dream-spoon-5

Activities

Exercise 5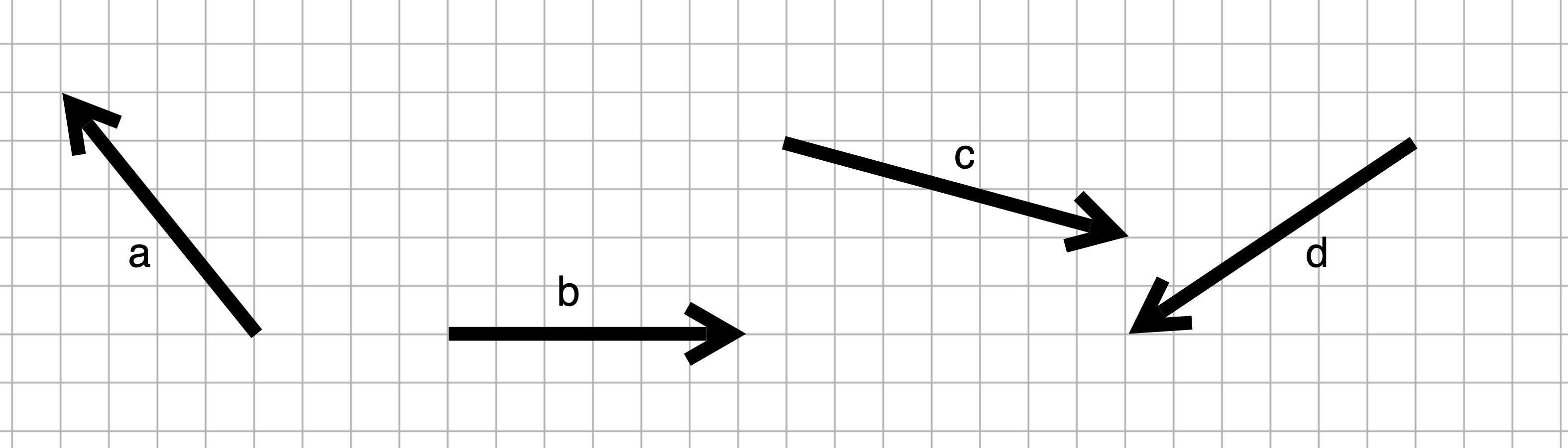

Refer to the vectors $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, and $\overrightarrow{d}$ above. Carry out the following projections graphically. You should show not only the result of the projection, but also the original vector being projected and the original vector being projected onto.

1. Project $\overrightarrow{a}$ onto $\overrightarrow{b}$
2. Project $\overrightarrow{c}$ onto $\overrightarrow{a}$
3. Project $\overrightarrow{b}$ onto itself.

Go back to your diagrams and add on to each diagram the residual vector from the projection. Make sure to use a different color ink or some other device to distinguish the residuals from the vectors you had already drawn.

Exercise 6 Construct a random 4-by-4 matrix named A whose columns are mutually orthogonal. Here’s the process:

1. Construct a vector with four elements that has random elements. A command to do so is

   1

   v1 <- cbind(rnorm(4))

   This will be the first column of the matrix.

2. Construct a new vector with random elements.

   1

   w <- cbind(rnorm(4))

   w will not be orthogonal to v1 as you can confirm by calculating the dot product between v1 and w. However, you can construct from the two vectors a new one that will be perpendicular to v1.

   1

   v2 <- w - (w %onto% v1)

3. Take the mutually orthogonal vectors you already have and package them into a matrix M. Then construct a new random vector w and project it onto M.

```{webr-r}
M <- cbind(v1, v2)
w <- cbind(rnorm(4))
v3 <- w - (w %onto% M)
```

Continue the process of step (iii) until you have 4 mutually orthogonal vectors, and collect them into the matrix `A`.

Use dot products to verify that v1, v2, v3, and v4 are mutually orthogonal.

Exercise 7  

1. Place a dot on a piece of paper. Hold a pencil perpendicular to the paper with the eraser on the dot. Now, (using a pen!) draw a vector on the paper that is perpendicular to the pencil. Now draw 5 more vectors, each different from the other, that are all perpendicular to the pencil.

2. Draw a vector $\overrightarrow{c}$ on the paper. Now draw another vector on the paper that is perpendicular to the first. Label it $\overrightarrow{a}$. Find another vector, to be labeled $\overrightarrow{b}$ that lies on the paper, is orthogonal to $\overrightarrow{c}$, and has a different direction from $\overrightarrow{a}$. It will turn out that $\overrightarrow{a}=k\overrightarrow{b}$. Write down the numerical value of the scalar $k$ for your $\overrightarrow{a}$ and $\overrightarrow{b}$.

3. Consider the vector $\overrightarrow{w}\equiv (2,5{)}^T$. Using only arithmetic, find some other vector $\overrightarrow{z}$ that is perpendicular to $\overrightarrow{w}$. (Hint: To be perpendicular, ${\overrightarrow{z}}^T\cdot \overrightarrow{w}$ must be zero. So make up two numbers such $a$ and $b$ such that $2a+5b=0$.) Write $\overrightarrow{z}$ on your paper.

4. Repeat (c) and create another vector ${\overrightarrow{z}}_2$ that is different from $\overrightarrow{z}$. Write ${\overrightarrow{z}}_2$ on your paper. In addition, find the scalar $k$ such that ${\overrightarrow{z}}_2=k\overrightarrow{z}$.

In the following exercises, you are asked to find numerical vectors that are perpendicular (“orthogonal”) to the stated vector. This is equivalent to finding a new vector whose dot product with the stated vector is zero. (Except … the new vector cannot be all zeros! The all-zero vector is exceptional and has no direction.) One effective strategy is to write down a vector consisting of a 1 in any position you like and zeros elsewhere. Find the dot product, calling it $d$. Then select one of the zeros to turn it non-zero. What value should it have? Just enough so that when included in the dot product it contributes $-d$.

5. Consider the vector $\overrightarrow{w}\equiv (1,2,-3,2{)}^T$.

   1. Find a vector $\overrightarrow{a}$ that is perpendicular to $\overrightarrow{w}$.
   2. Find another vector $\overrightarrow{b}$ that is perpendicular both to $\overrightarrow{w}$ and to $\overrightarrow{a}$. (Hint: It can be done.)
   3. Create yet another vector $\overrightarrow{c}$ that is a linear combination of $\overrightarrow{a}$ and $\overrightarrow{b}$. (You can choose whatever combination you like, but both coefficients should be non-zero.) What is the angle between $\overrightarrow{c}$ and $\overrightarrow{w}$?

6. You have been sent on a mission to 5-dimensional space. Your task is to find a vector that is perpendicular to $\overrightarrow{w}\equiv (2,1,3,3,-4{)}^T$. Do so.

7. BONUS. Find as many vectors as you can that are perpendicular to $\overrightarrow{w}\equiv (2,1,3,3,-4{)}^T$ and to each other. The arithmetic will not necessarily be easy. When you give up (with honor!), figure out how many mutually perpendicular vectors there can be in 5-dimensional space. How about 10-dimensional space?

Exercise 8 In physics and engineering, there is a very important operation called the cross product and written $\overrightarrow{u}\times \overrightarrow{v}$. The operation is only defined for vectors in 3-dimensional space. The output of the cross product is another 3-dimensional vector which can be calculated arithmetically as:

$$\left(\begin{array}{c}a\\ b\\ c\end{array}\right)\times \left(\begin{array}{c}e\\ f\\ g\end{array}\right)\equiv \left(\begin{array}{c}bg-cf\\ ce-ag\\ af-be\end{array}\right)$$

Make up coordinates for two three-dimensional vectors $\overrightarrow{u}$ and $\overrightarrow{v}$ that point in different directions.

Calculate the cross product $\overrightarrow{w}\equiv \overrightarrow{u}\times \overrightarrow{v}$.

1. Find the angle between $\overrightarrow{w}$ and $\overrightarrow{u}$.
2. Find the angle between $\overrightarrow{w}$ and $\overrightarrow{v}$.

Other than this brief description, we will not use cross products at all in this course. But keep them in mind for your upcoming physics and engineering courses.

30-exercises.rmarkdown

No answers yet collected