Chap 29 Exercises

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1 Here are 12 vectors, labeled “a” through “m.” (Letter “i” has been left out.) There are several quick questions, each of which makes a claim about whether the sum of two vectors equals a third. Answer true or false to the claim. There are no tricks about exactitude, so if the claim is close to being true, answer true.

Figure 1
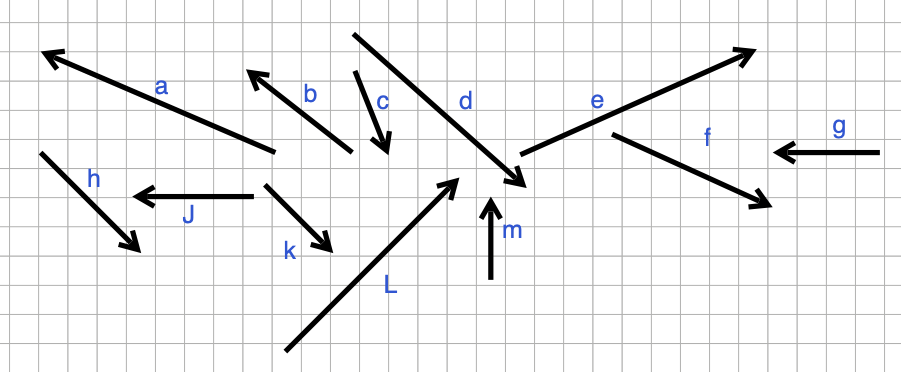
  1. \(\vec{a} + \vec{b} = \vec{L}\)
True       False      

question id: titmouse-stand-pantry-1

  1. \(\vec{b} + \vec{J} = \vec{a}\)
True       False      

question id: titmouse-stand-pantry-2

  1. \(\vec{b} + \vec{m} = \vec{J}\)
True       False      

question id: titmouse-stand-pantry-3

  1. \(\vec{c} + \vec{f} = \vec{d}\)
True       False      

question id: titmouse-stand-pantry-4

  1. \(\vec{k} + \vec{L} = \vec{e}\)
True       False      

question id: titmouse-stand-pantry-5

  1. \(\vec{e} + \vec{b} = \vec{m}\)
True       False      

question id: titmouse-stand-pantry-6

  1. \(\vec{m} + \vec{g} = \vec{b}\)
True       False      

question id: titmouse-stand-pantry-7

Exercise 2 Consider these vectors:

\[\vec{u} \equiv \left[\begin{array}{r} -81382\\ -9645\\ -5099\end{array}\right]\ \ \ \vec{v} \equiv \left[\begin{array}{r}\ 61713\\ -45063\\ -51427\end{array}\right]\ \ \ \vec{w} \equiv \left[\begin{array}{r}\ 90176\\\ 57269\\ -27150\end{array}\right]\] \[\vec{x} \equiv \left[\begin{array}{r} -93470\\ -85812\\\ 93693\end{array}\right]\ \ \ \vec{y} \equiv \left[\begin{array}{r}\ 14751\\\ 65466\end{array}\right]\ \ \ \vec{z} \equiv \left[\begin{array}{r}\ 30370\\\ 645\\ -45350\end{array}\right]\]

In Active R chunk lst-calf-pitch-chair, construct R versions of the above vectors, named u through z.

Active R chunk 1

Then, using R, construct these linear combinations.

  1. \(\ \ \ \ \vec{u} + 2 \vec{v}\)

\((42044, -99771, 54300)^T\)

\((42044, -99771, -107953)^T\)

\((42044, 99771, -54300)^T\)

invalid combination

question id: calf-pitch-chair-1

  1. \(\ \ \ \ 6 \vec{y} - 4\vec{z}\)

\((111752, 10290, -40251)^T\)

\((111752, 10290, 40251)^T\)

\((111752, -10290, -40251)^T\)

invalid combination

question id: calf-pitch-chair-2

  1. \(\ \ \ \ -2 \vec{w} + 0 \vec{u}\)

\((-180532, -99771, 54300)^T\)

\((-180532, -24446, 54300)^T\)

\((-180532, -24969, 54300)^T\)

invalid combination

question id: calf-pitch-chair-3

  1. \(\ \ \ \ - \vec{z} - \vec{u}\)

\((111752, -244496, 54300)^T\)

\((111752, 10290, -40251)^T\)

\((111752, -244496, -173698)^T\)

invalid-combination

question id: calf-pitch-chair-4

  1. \(\ \ \ \ \vec{u} + \vec{y}\)

\((-341248, 10290, -40251)^T\)

\((-180532, -244496, 54300)^T\)

\((-341248, -244496, -173698)^T\)

invalid combination

question id: calf-pitch-chair-5

  1. \(\ \ \ \ 2 \vec{u} - 4\vec{w} + 6 \vec{z}\)

\((-341248, 10290, -40251)^T\)

\((-180532, -244496, 54300)^T\)

\((-341248, -244496, -173698)^T\)

invalid combination

question id: calf-pitch-chair-6

Exercise 3 Locating WW I aircraft

The photograph shows part of an aircraft detection system from World War I. The concrete block is an “acoustic mirror.” Its purpose is to collect and reflect sound from an aircraft, concentrating them at a point where they can be picked up by a microphone. Moving the microphone to a point where the concentrated sound is strongest allows the aircraft’s bearing to be identified, helping observers acquire the aircraft visually.

Source

Figure fig-cat-understand-car-2 shows how, with two or more such acoustic mirrors, the location of the aircraft can be identified.

Figure 2

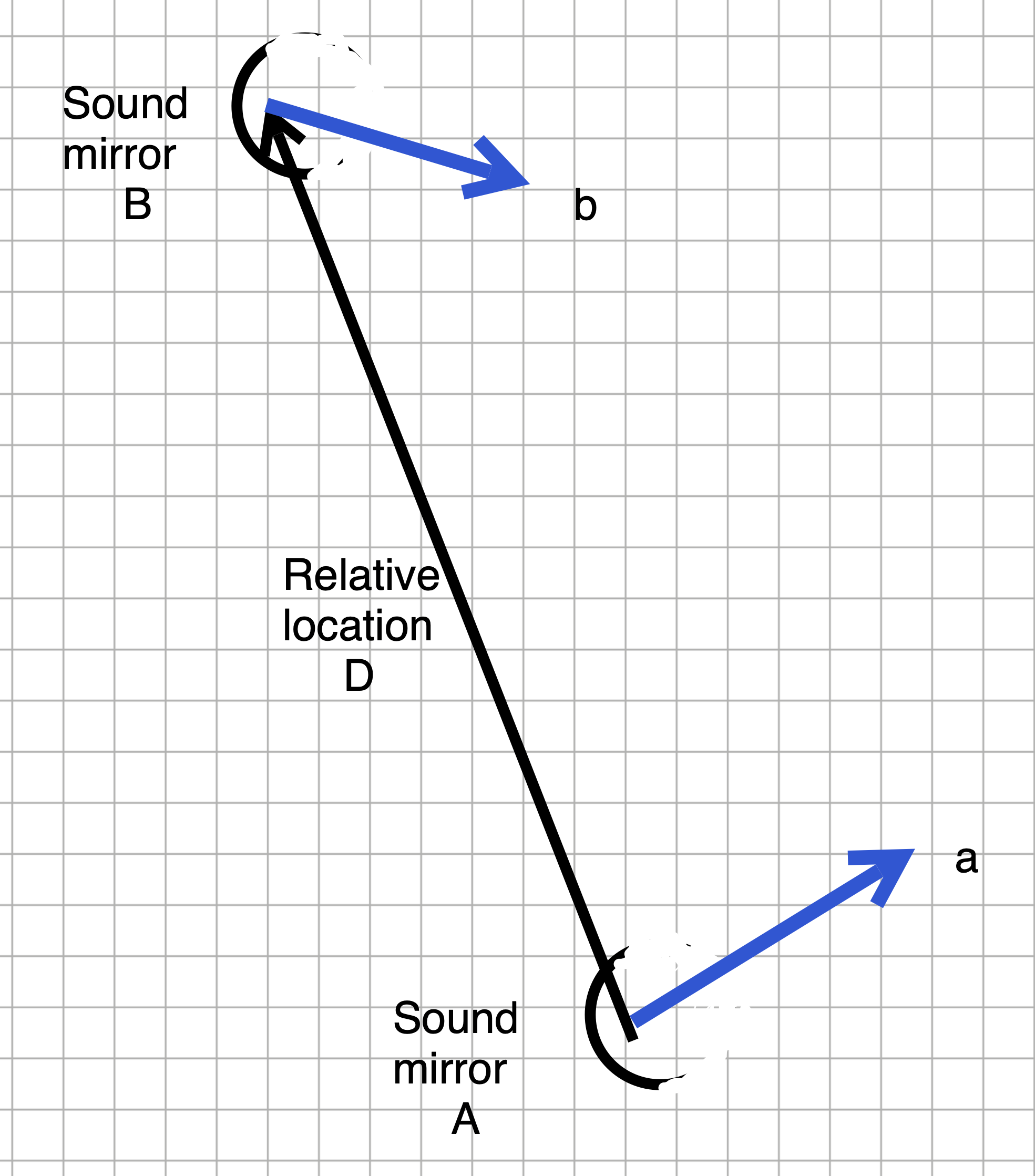
Give the position of the aircraft as a multiple of \(\vec{a}\) from sound mirror A and as a multiple of \(\vec{b}\) from sound mirror B. (Choose the closest answer)

\(3 \vec{a}\) and \(4.5 \vec{b}\)

\(4 \vec{a}\) and \(6 \vec{b}\)

\(3\vec{a}\) and \(2 \vec{b}\)

\(4\vec{a}\) and \(4.5\vec{b}\)

question id: g4ZZQz

Exercise 4  

  1. What’s the result of this multiplication:\[\left[\begin{array}{rr}-1 & \frac{3}{4}\\1 & 0\end{array}\right] \cdot \left[\begin{array}{r}2\\1 \end{array}\right] ?\]

\(\left[\begin{array}{r}-\frac{5}{4}\\2 \end{array}\right]\)

\(\left[\begin{array}{r}\frac{5}{4}\\\frac{1}{4} \end{array}\right]\)

\(\left[\begin{array}{r}-\frac{3}{4}\\2 \end{array}\right]\)

\(\left[\begin{array}{r}\frac{3}{4}\\-2 \end{array}\right]\)

question id: shark-understand-saw-1

  1. What’s the result of this multiplication:\[\left[\begin{array}{rr}3 & 4\\1 & 0\end{array}\right] \cdot \left[\begin{array}{r}-5\\6 \end{array}\right] ?\]

\(\left[\begin{array}{r}9\\-5 \end{array}\right]\)

\(\left[\begin{array}{r}9\\5 \end{array}\right]\)

\(\left[\begin{array}{r}-7\\5 \end{array}\right]\)

\(\left[\begin{array}{r}-7\\-5 \end{array}\right]\)

question id: shark-understand-saw-2

  1. What’s the result of this multiplication:\[\left[\begin{array}{rr}0 & -2\\1 & 0\end{array}\right] \cdot \left[\begin{array}{r}12.62\\-7.14 \end{array}\right] ?\]

\(\left[\begin{array}{r}14.28\\12.62 \end{array}\right]\)

\(\left[\begin{array}{r}-14.28\\12.62 \end{array}\right]\)

\(\left[\begin{array}{r}14.28\\-12.62 \end{array}\right]\)

\(\left[\begin{array}{r}12.62\\-12.62 \end{array}\right]\)

question id: shark-understand-saw-3

  1. All of these vectors point in the same (or exactly opposite) direction, except one:\[ {\mathbf v}_1 = \left[\begin{array}{r}7.2\\-2.4\end{array}\right], \ \ {\mathbf v}_2 = \left[\begin{array}{r}3.6\\1.2\end{array}\right],\ \ {\mathbf v}_3 = \left[\begin{array}{r}3.6\\-1.2\end{array}\right],\ \ {\mathbf v}_4 = \left[\begin{array}{r}-1.8\\0.6\end{array}\right] \] Which is the one exception?

\({\mathbf v}_1\)

\({\mathbf v}_2\)

\({\mathbf v}_3\)

\({\mathbf v}_4\)

question id: shark-understand-saw-4

  1. All of these vectors point in the same (or exactly opposite) direction, except one:\[ {\mathbf u}_1 = \left[\begin{array}{r}\sqrt{2}/2\\\sqrt{12}\end{array}\right], \ \ {\mathbf u}_2 = \left[\begin{array}{r}1/\sqrt{2}\\2\sqrt{3}\end{array}\right],\ \ {\mathbf u}_3 = \left[\begin{array}{r}-1/\sqrt{2}\\-\sqrt{2}\sqrt{6}\end{array}\right],\ \ {\mathbf u}_4 = \left[\begin{array}{r}\sqrt{2}/4\\\sqrt{6}\end{array}\right],\ \ {\mathbf u}_5 = \left[\begin{array}{r}\sqrt{2}/4\\\sqrt{3}\end{array}\right] \] Which is the one exception?

\({\mathbf u}_1\)

\({\mathbf u}_2\)

\({\mathbf u}_3\)

\({\mathbf u}_4\)

\({\mathbf u}_5\)

question id: shark-understand-saw-5

Activities

Exercise 5 Copy onto paper the vectors and their labels from Figure fig-squirrel-hear-glasses. Any good approximation will do.

Figure 3

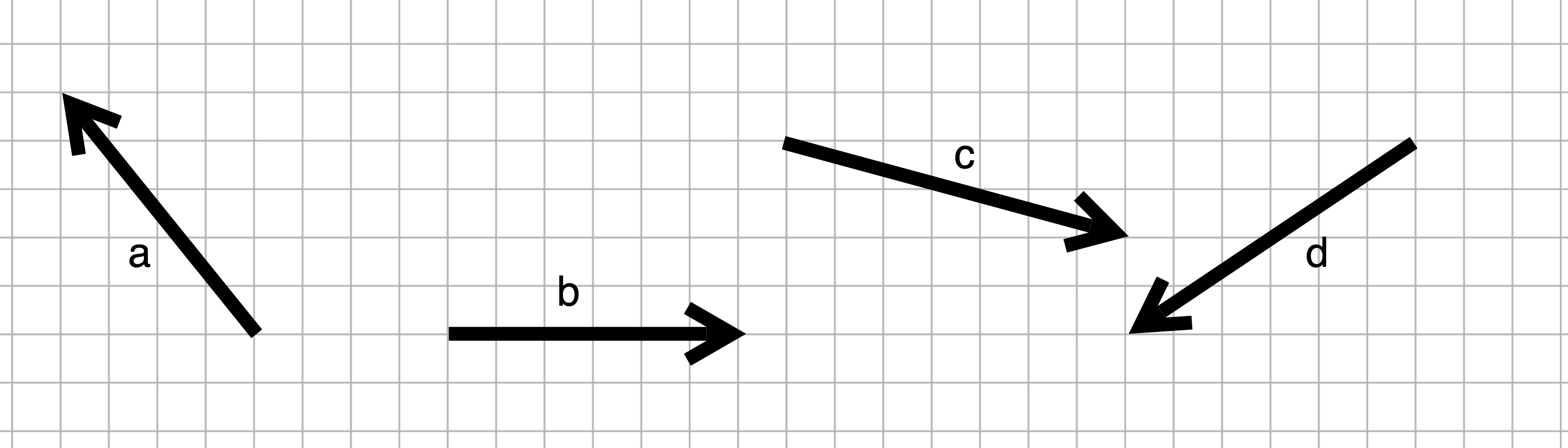
Then, on the paper …

  1. Draw (and label with the Roman numeral) the following vector additions and subtractions. (You should “show your work” by putting the vectors being added in the diagram along with the result of the addition.)
  1. \(\vec{a} + \vec{b}\)
  2. \(\vec{c} + \vec{d}\)
  3. \(\vec{d} + \vec{b} + \vec{a}\)
  4. \(\vec{b} - \vec{a}\)
  1. Construct these linear combinations. Your diagram should show both the scaled vectors being added and the output of the linear combination.

A. \(\ \ \ \ 2 \vec{a} + 1 \vec{b}\) B. \(\ \ \ \ 1.5 \vec{c} - 2 \vec{d}\) C. \(\ \ \ \ - \vec{b} + 2\vec{c} + 3\vec{d}\)

Exercise 6 Figure fig-sun-direction is a kind of treasure map. The starting point (the flagpole) is in the center of the map.

Figure 4: For June 1: \(\color{magenta}{\text{Sun's direction at 6:32}}\) and $$. (Location: latitude 38.0091, /longitude -104.8871). Source: suncalc.org

Find the treasure according to the instructions given in the text: 213 paces away from the sun at 6:32, then 126 paces toward the sun at 12:19.

For scale, a small part of the grid is shown below. Assume that each square of the grid is 15 paces on a side.

Exercise 7 Define the vector \[\vec{v} \equiv \left[\begin{array}{r}4\\1\\3\\-2\end{array}\right]\ .\]

Your task is to construct different vectors that are orthogonal to \(\vec{v}\). You can use the trick presented in sec-orthogonality of creating templates with zero in all but two of the positions, e.g. \[\left[\begin{array}{r}0\\0\\\_\\\_\end{array}\right] \ \ \text{or}\ \ \ \left[\begin{array}{r}0\\\_\\0\\\_\end{array}\right] \ \ \text{and}\ \ \ \left[\begin{array}{r}\_\\\_\\0\\0\end{array}\right]\] To construct a vector orthogonal to \(\vec{v}\), fill in the blanks by taking the corresponding elements of \(\vec{v}\), swapping them, and negating one of them. For example, taking the first template will produce

\[\left[\begin{array}{c}0\\0\\\underline{\ 2\ }\\\underline{\ 3\ }\end{array}\right]\ .\]

  1. Fill in the blanks of the other two tempates to create vectors orthogonal to \(\vec{v}\).

  2. Construct 3 new vectors by taking different linear combinations of the vectors you created in (A). Are any of these new vectors orthogonal to \(\vec{v}\)? Show your work.

  3. Prove algebraically that any linear combination of a set of vectors orthogonal to \(\vec{x}\) will itself be orthogonal to \(\vec{x}\).

No answers yet collected