question id: fox-knows-dress-1
Chap 22 Exercises
\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]
Exercise 1 Consider the following functions, all of which involve a domain split at \(x=0\) and the pasting together of two individually \(C^\infty\) functions:
\[f_A(x) \equiv \left\{\begin{array}{cl}{{x^2}} & \text{for}\ 0\leq x\\ x& \text{otherwise}\end{array} \right.\]
- How smooth is \(f_A(x)\)?
\[f_B(x) \equiv \left\{\begin{array}{cl}x^3 & \text{for}\ 0 \leq x\\0&\text{otherwise}\end{array} \right.\]
- How smooth is \(f_B(x)\)?
question id: fox-knows-dress-2
\[f_C(x) \equiv \left\{\begin{array}{cl}{x^3} & \text{for}\ 0 \leq x\\x^3& \text{otherwise}\end{array} \right.\]
- How smooth is \(f_C(x)\)?)
question id: fox-knows-dress-3
\[f_D(x) \equiv \left\{\begin{array}{cl}x^3 & \text{for}\ 0 \leq x\\x^2&\text{otherwise}\end{array} \right.\]
- How smooth is \(f_D(x)\)?
question id: fox-knows-dress-4
\[f_E(x) \equiv \left\{\begin{array}{cl}x^3 & \text{for}\ 0 \leq x\\-x^2 &\text{otherwise}\end{array} \right.\]
- How smooth is \(f_E(x)\)?
question id: fox-knows-dress-5
\[f_F(x) \equiv \left\{\begin{array}{cl}\cos(x) & \text{for}\ 0 \leq x\\0 &\text{otherwise}\end{array} \right.\]
- How smooth is \(f_F(x)\)?
question id: fox-knows-dress-6
\[f_G(x) \equiv \left\{\begin{array}{cl}\sin(x) & \text{for}\ 0 \leq x\\0 &\text{otherwise}\end{array} \right.\]
- How smooth is \(f_G(x)\)?
question id: fox-knows-dress-7
\[f_H(x) \equiv \left\{\begin{array}{cl}\sin(x) & \text{for}\ 0 \leq x\\x &\text{otherwise}\end{array} \right.\]
- How smooth is \(f_H(x)\)?
question id: fox-knows-dress-8
Exercise 2
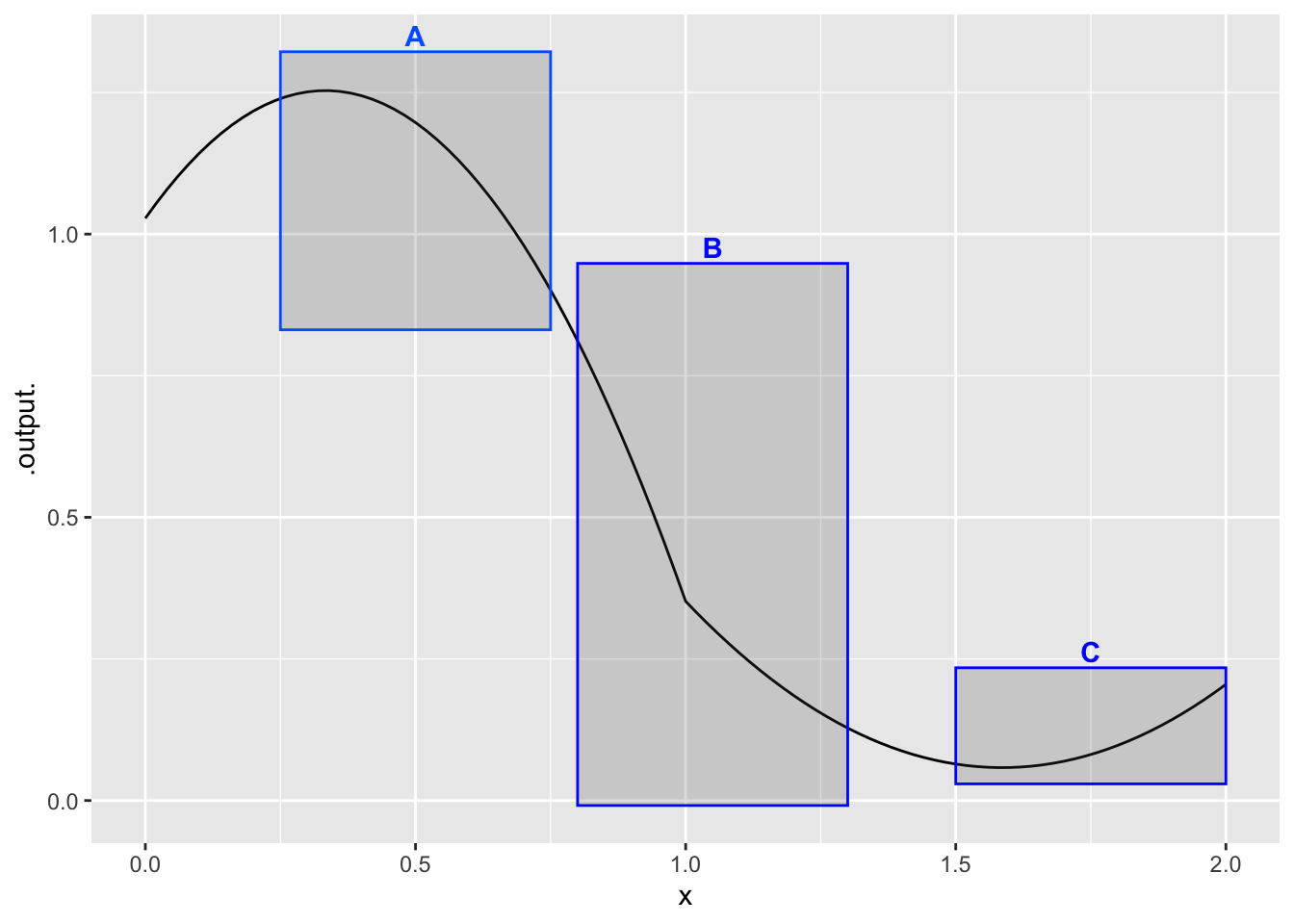
- In which boxes is the function shown in #fig-panda-drive-shirt-1 smooth?
question id: panda-drive-shirt-1
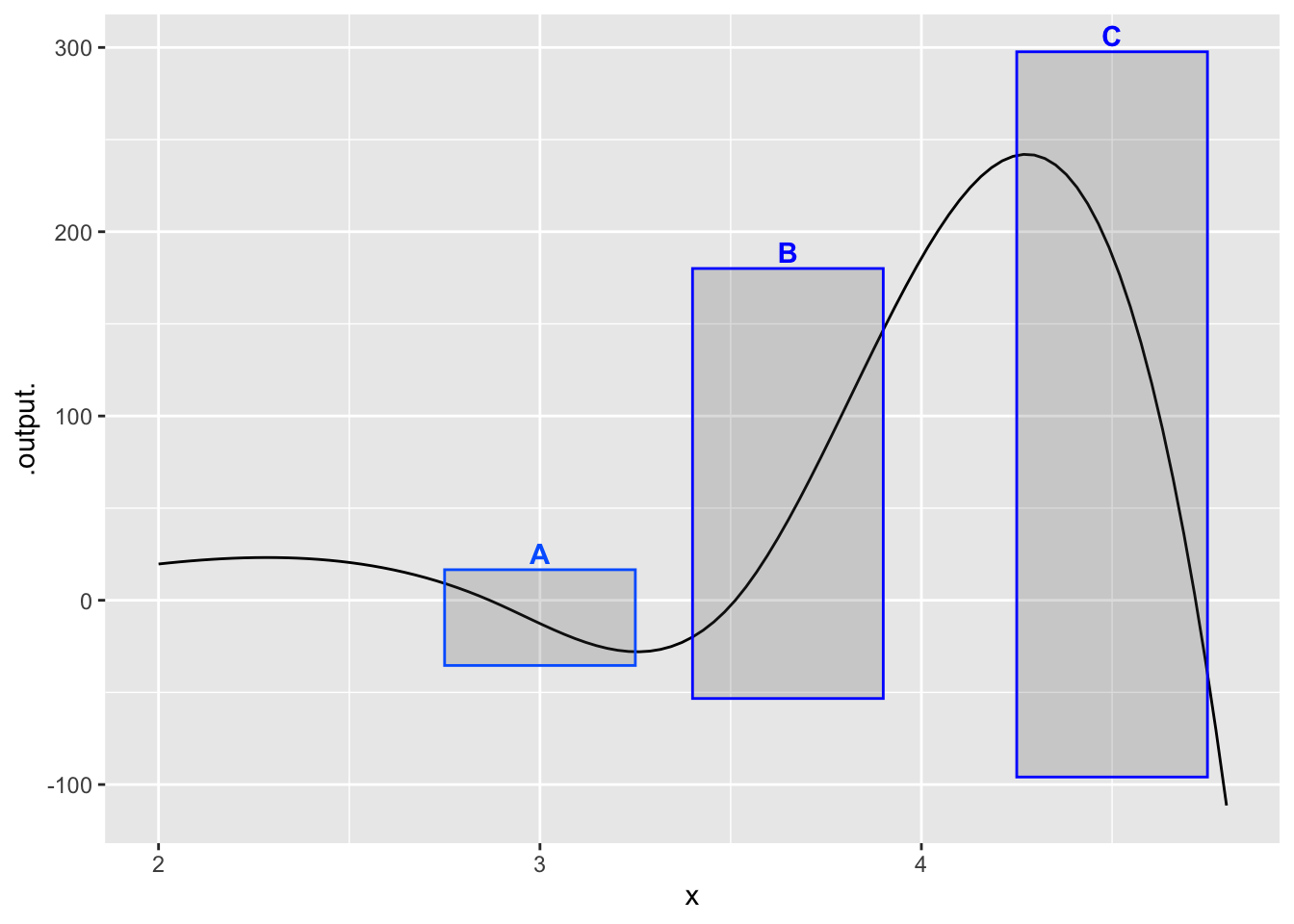
2.In which boxes is the function in Figure 2 smooth?
question id: panda-drive-shirt-2
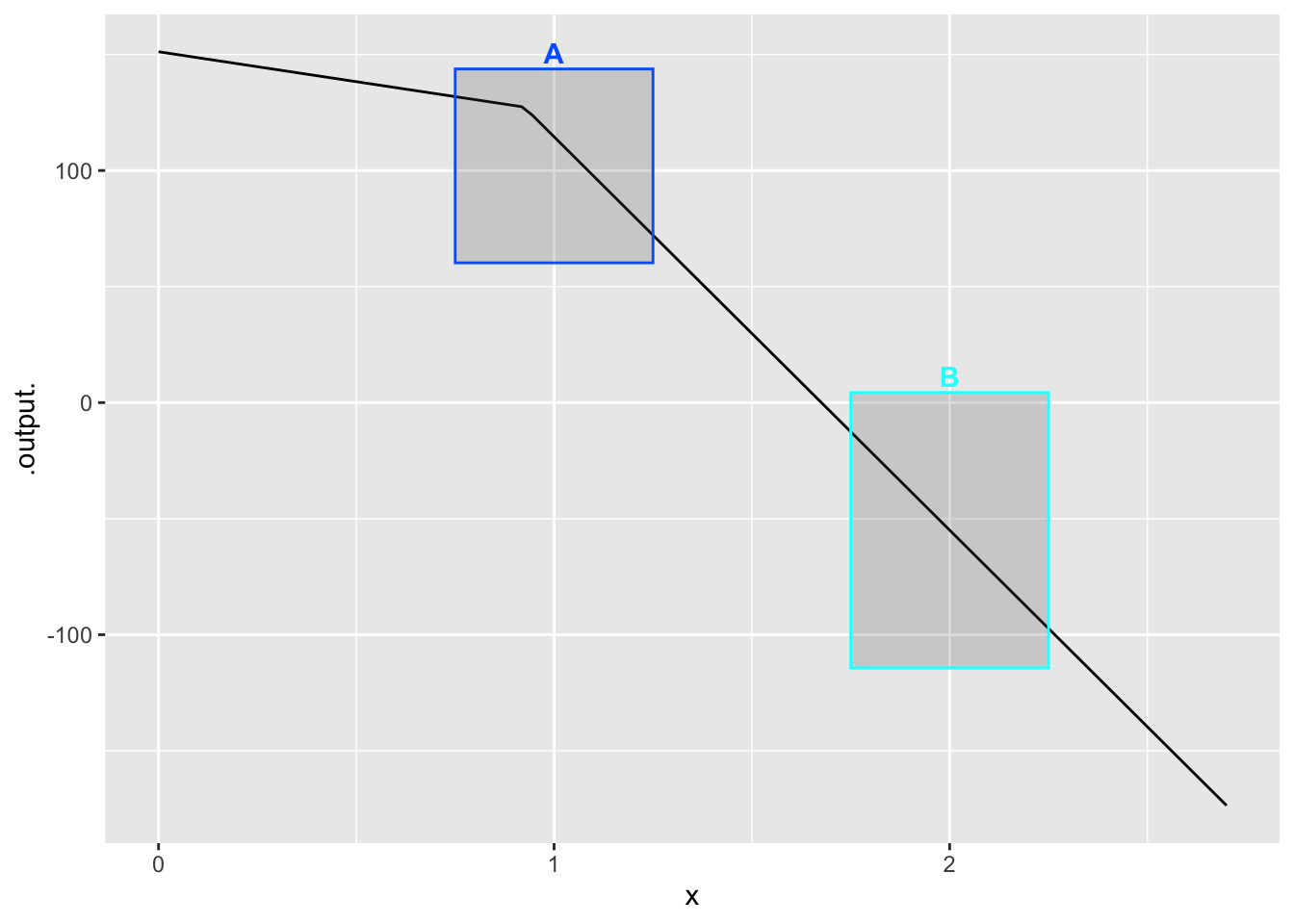
- In which boxes is the function in @?fig-panda-drive-shirt-3 is smooth?
question id: panda-drive-shirt-3
Exercise 3 For the sketched functions below, decide what level of smoothness—\(C^0, C^1, C^2, ...\)— best describes the function. (We make no tricks in the drawings. Where a function looks like it is broken–that is, the function locally has a V-shape or a \(\Lambda\)-shape–it is meant to be broken.)
- What’s the smoothness level of function A(x)? (Hint: A quadratic function has a first derivative that changes with x but a second derivative that is constant for all x.)
question id: moose-hears-door

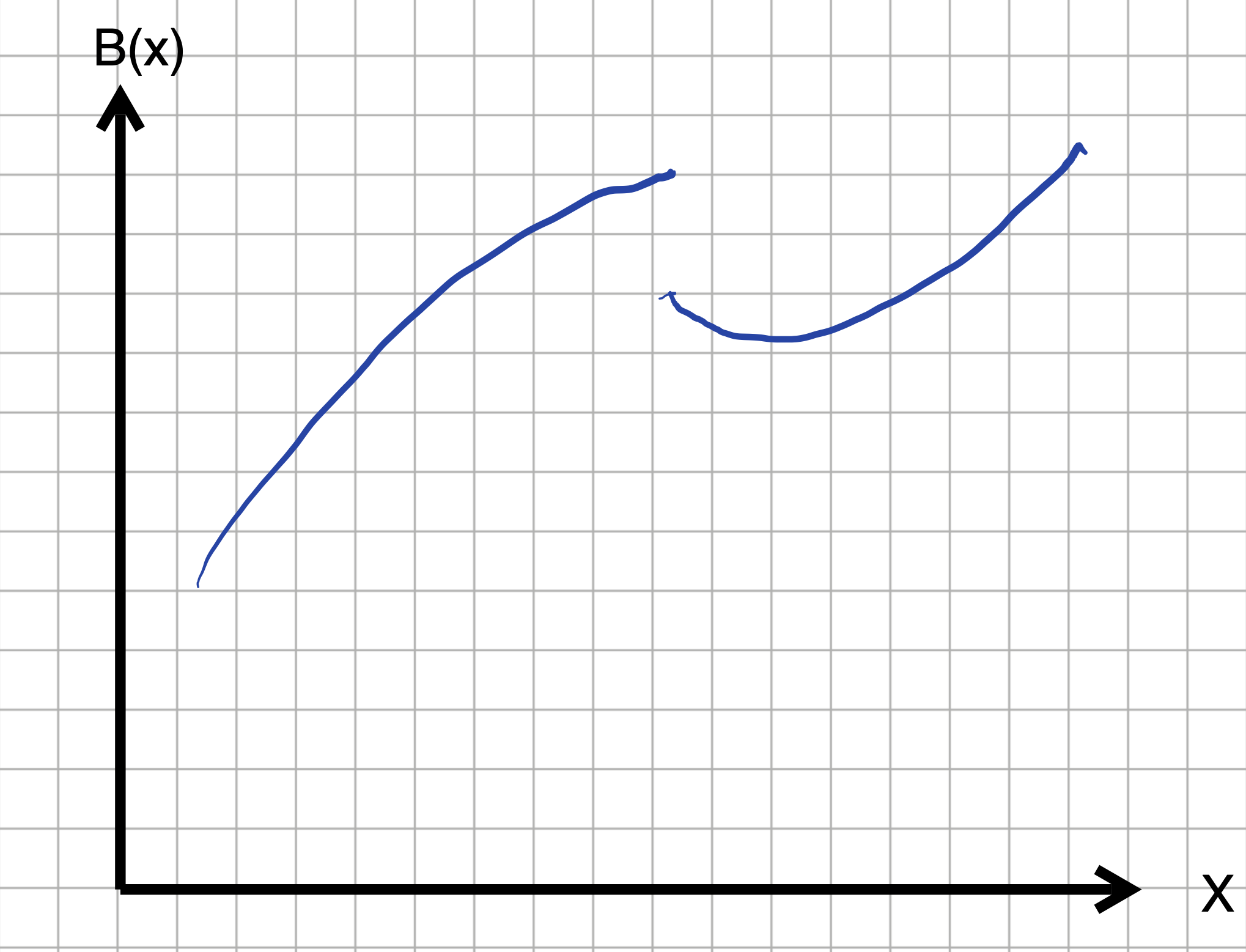
- What’s the smoothness level of function B(x)?
question id: moose-hears-door-2
- What’s the smoothness level of function C(x)?
question id: moose-hears-door-4
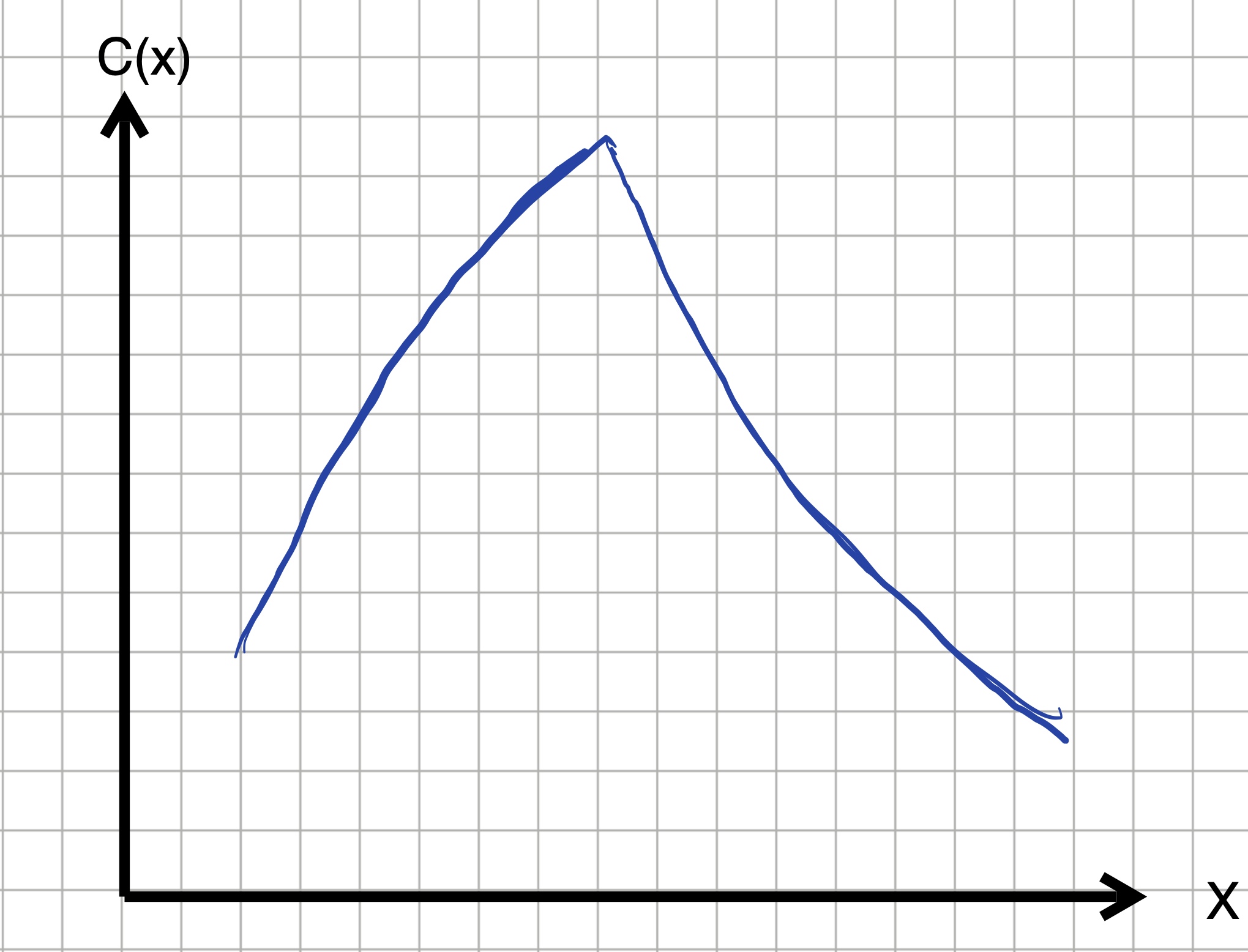
- What’s the smoothness level of function D(x)?
question id: mose-hears-door-4
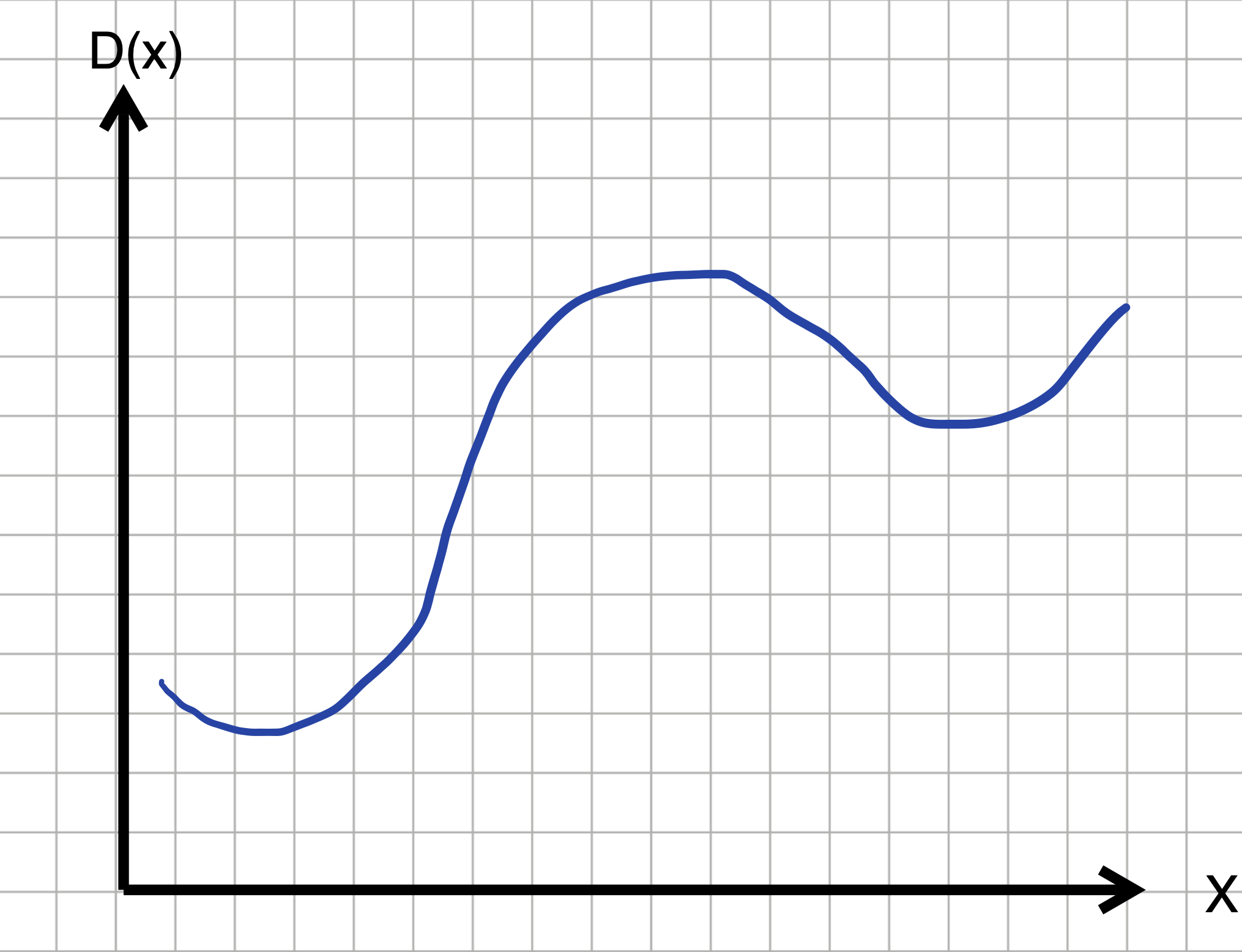
Activities
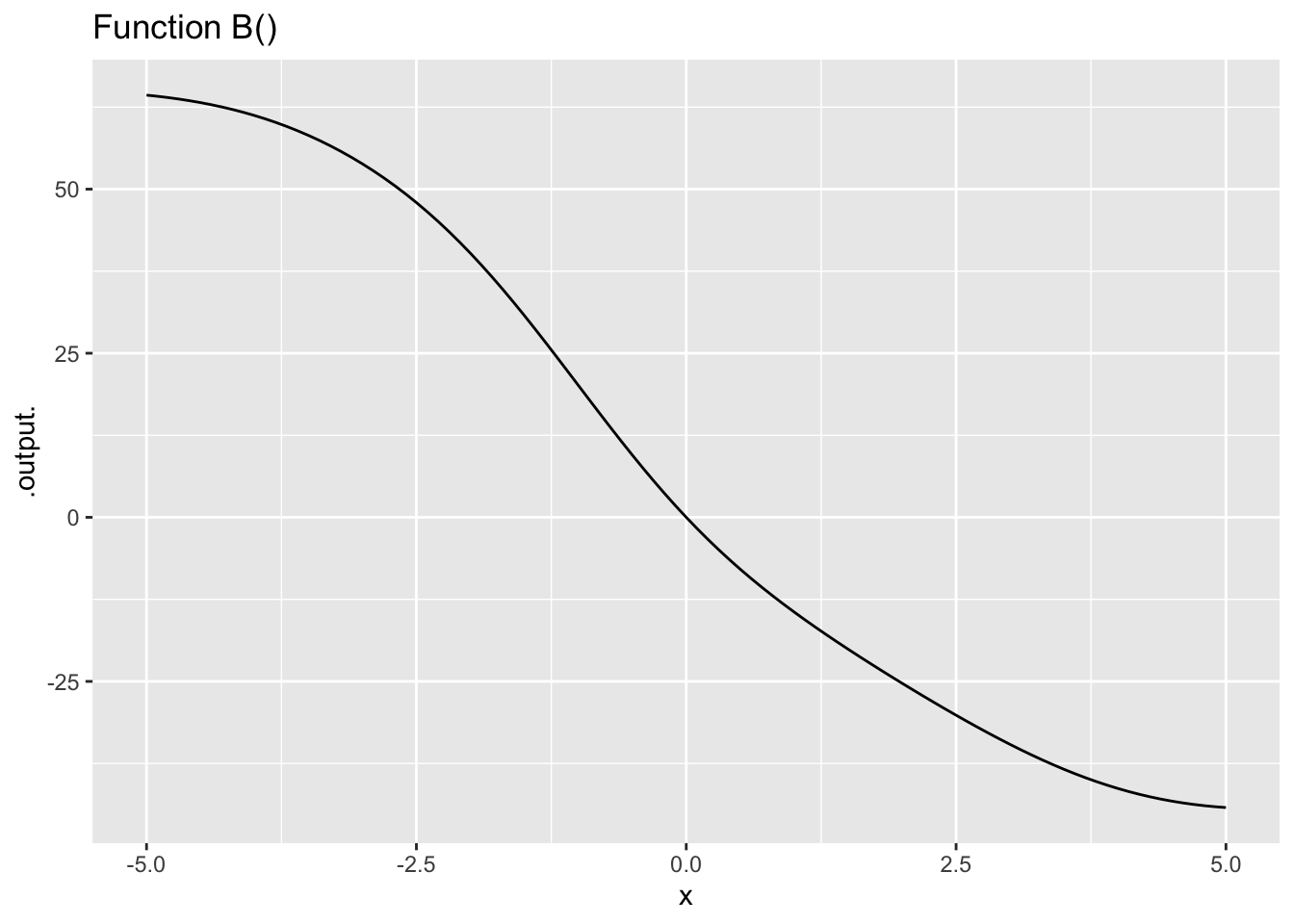
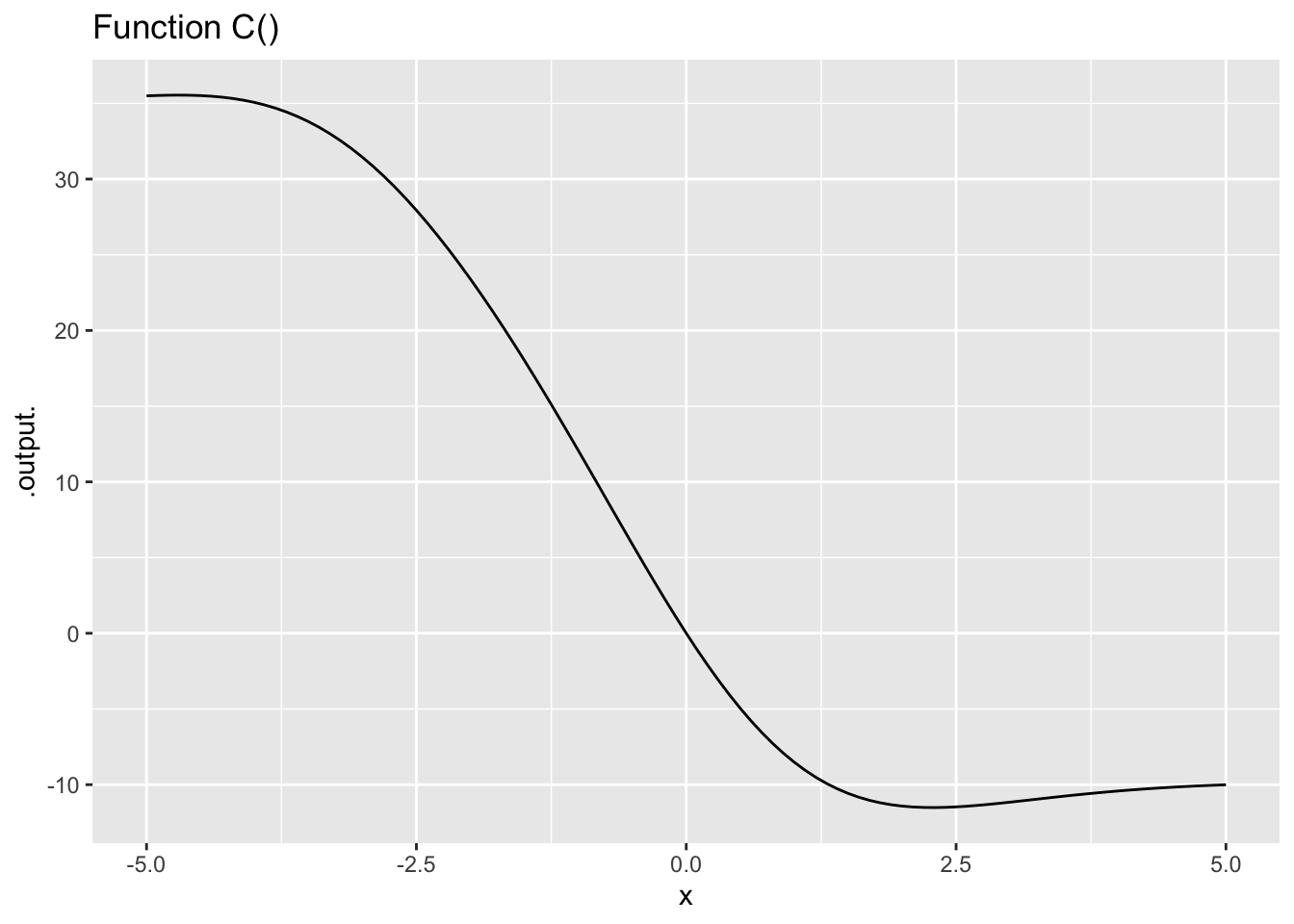
Exercise 4 The left column in Figure 3 shows functions A(), B(), C(), and D(). The right column shows functions dd1(), dd2(), and so on. Find which function (if any) in the right column corresponds to the 2nd derivative of a function in the left column.
Remember the concepts of “concave up” (a smile!) and “concave down” (a frown). At those values of \(x\) for which the 2nd derivative of a given function is positive, the given function will be concave up. When the 2nd derivative is negative, the given function will be concave down.
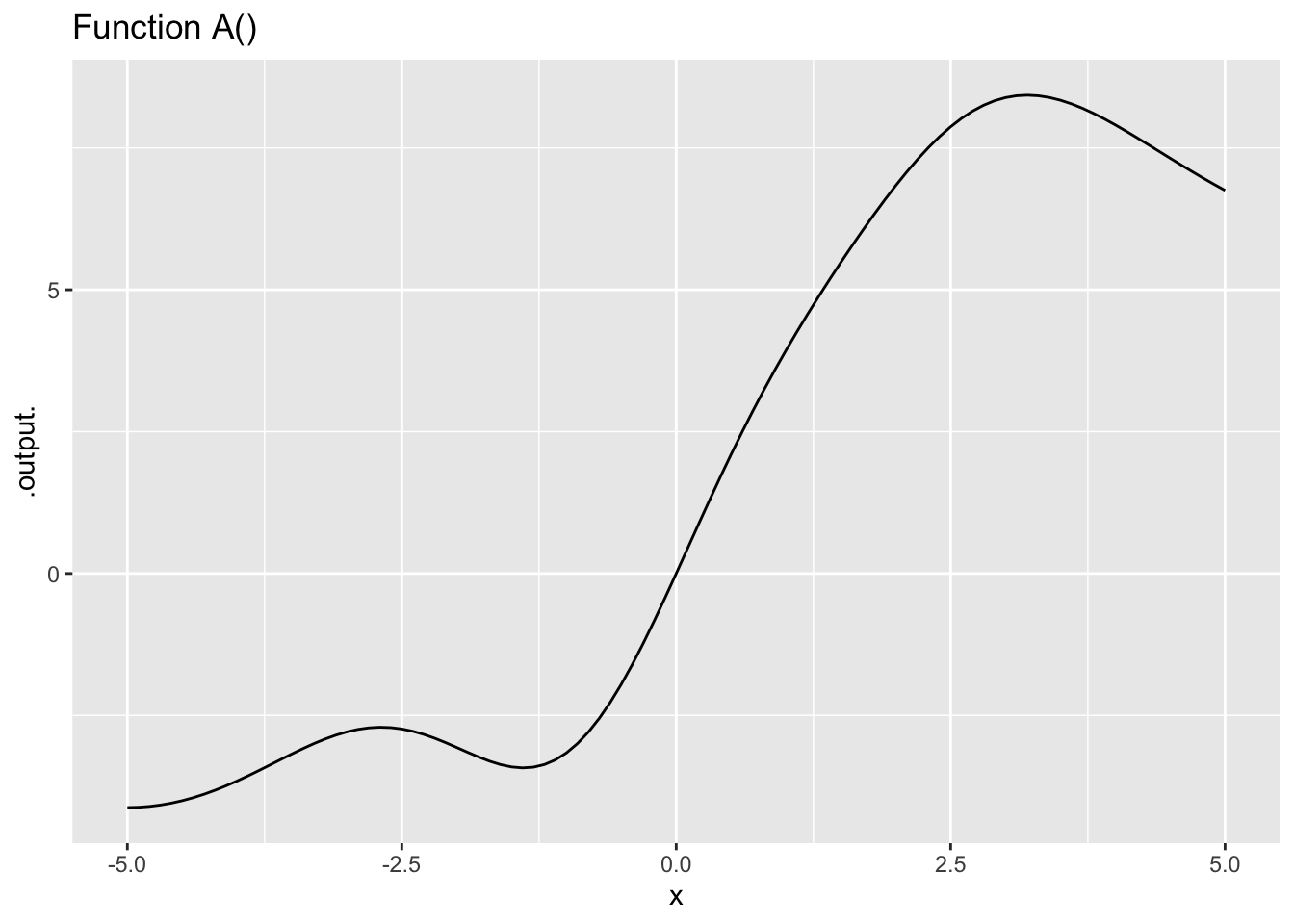
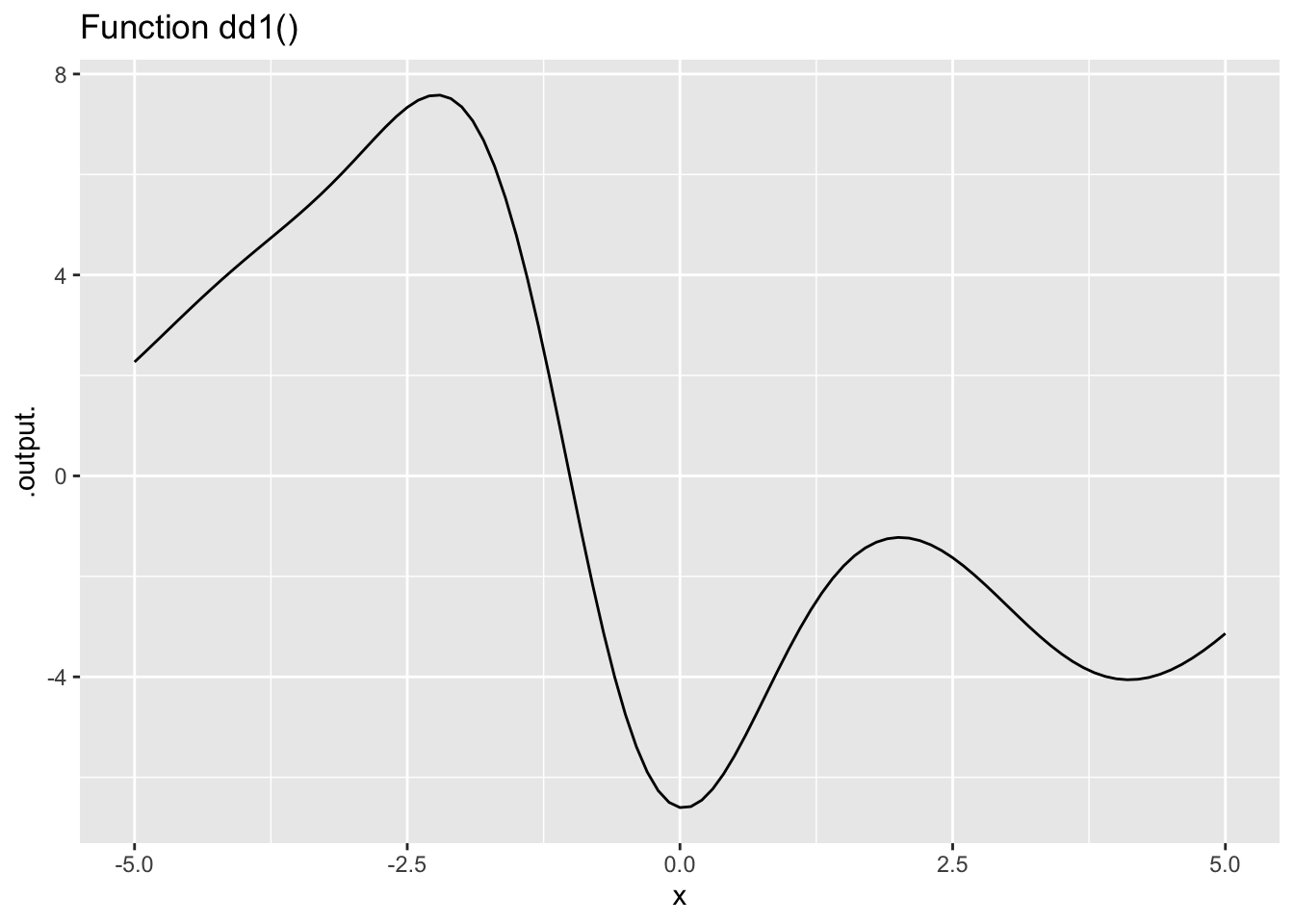
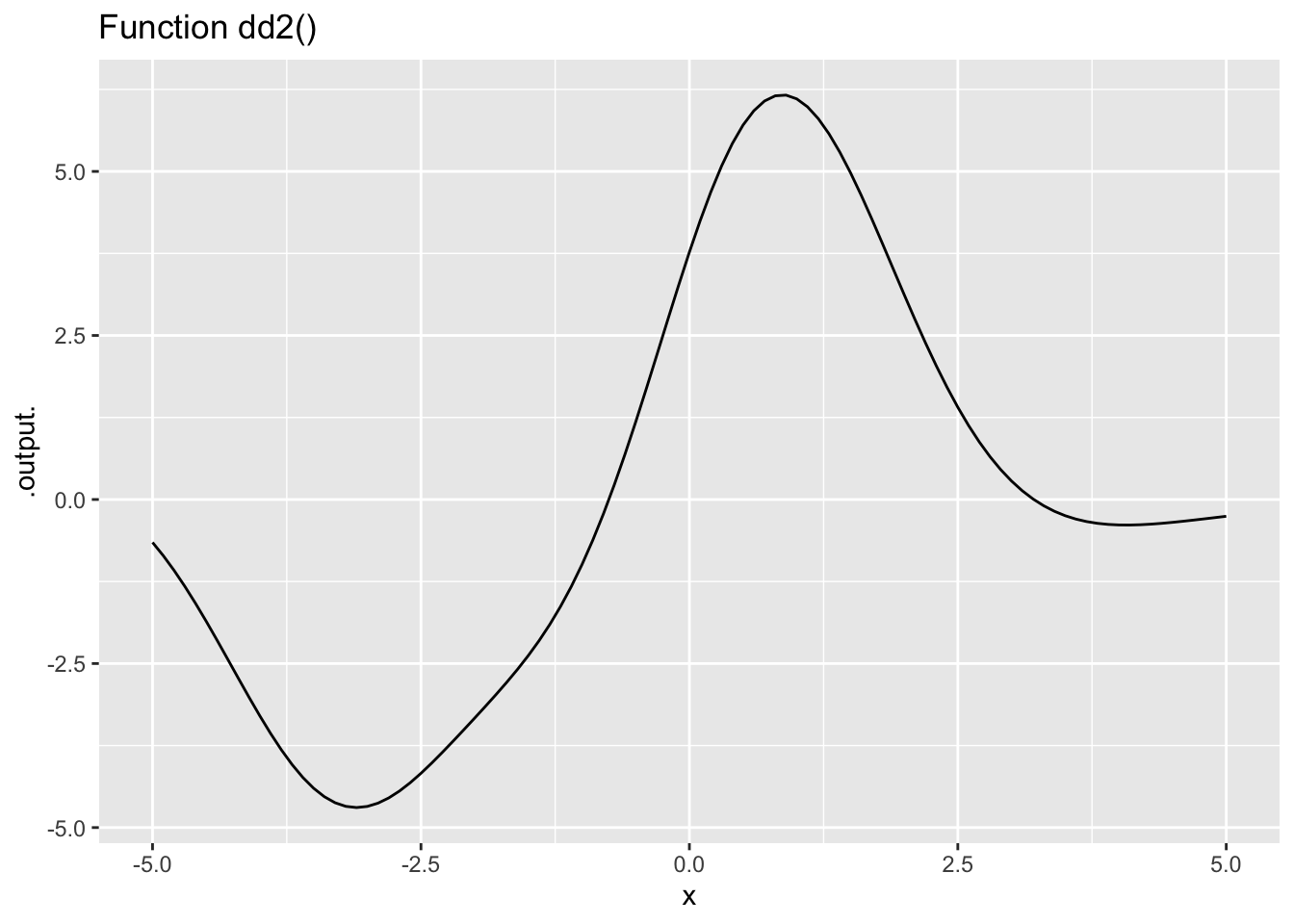
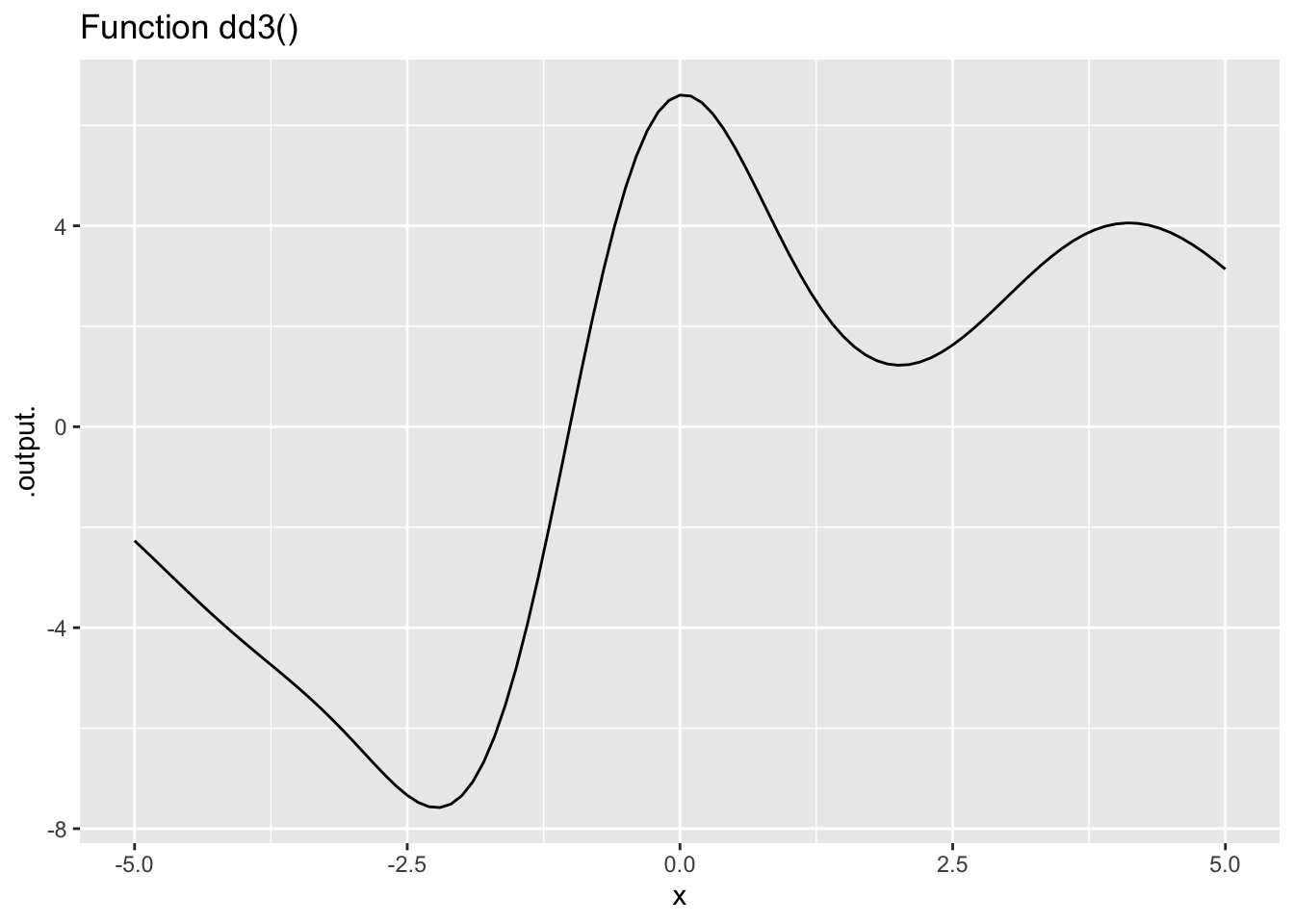
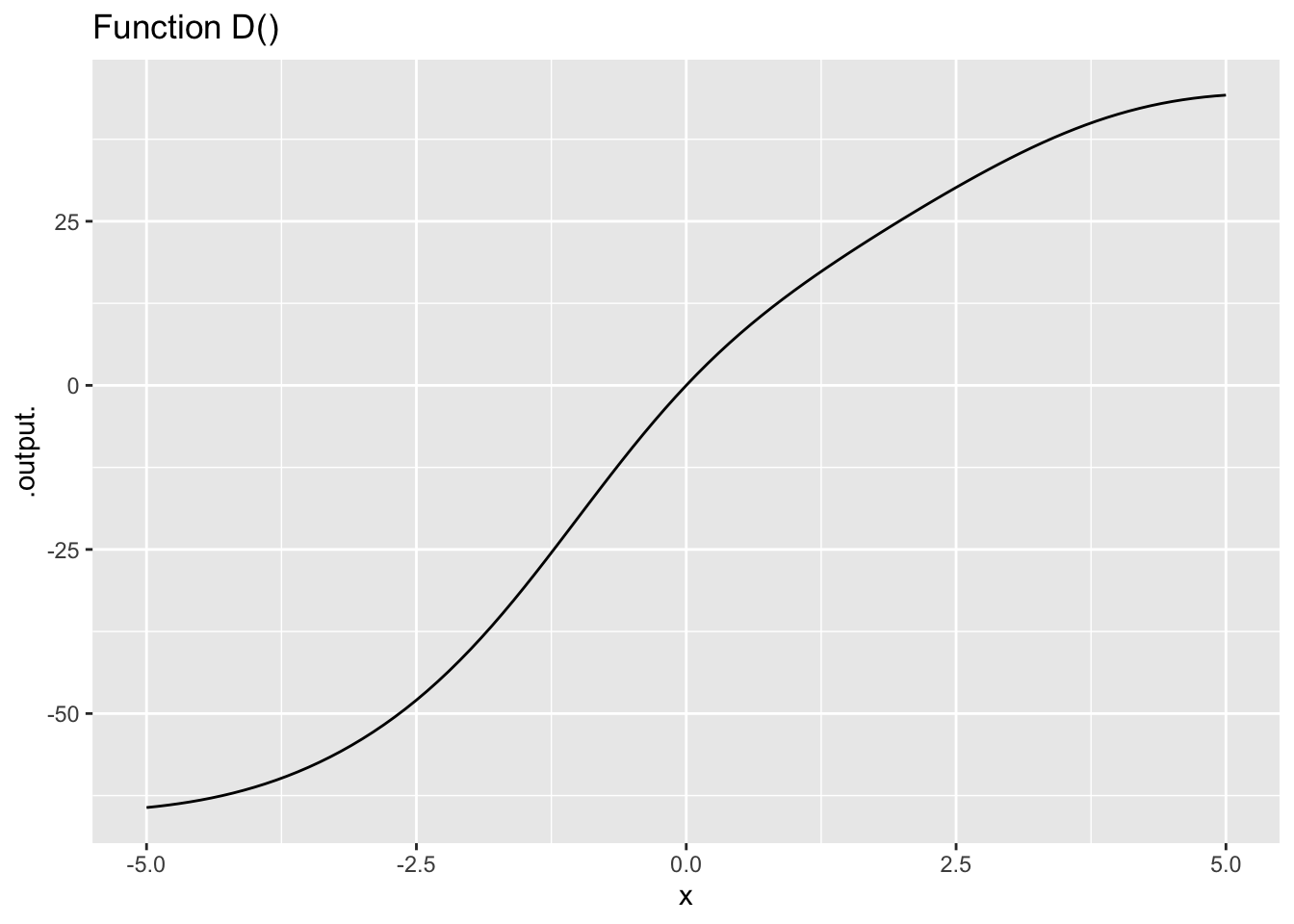
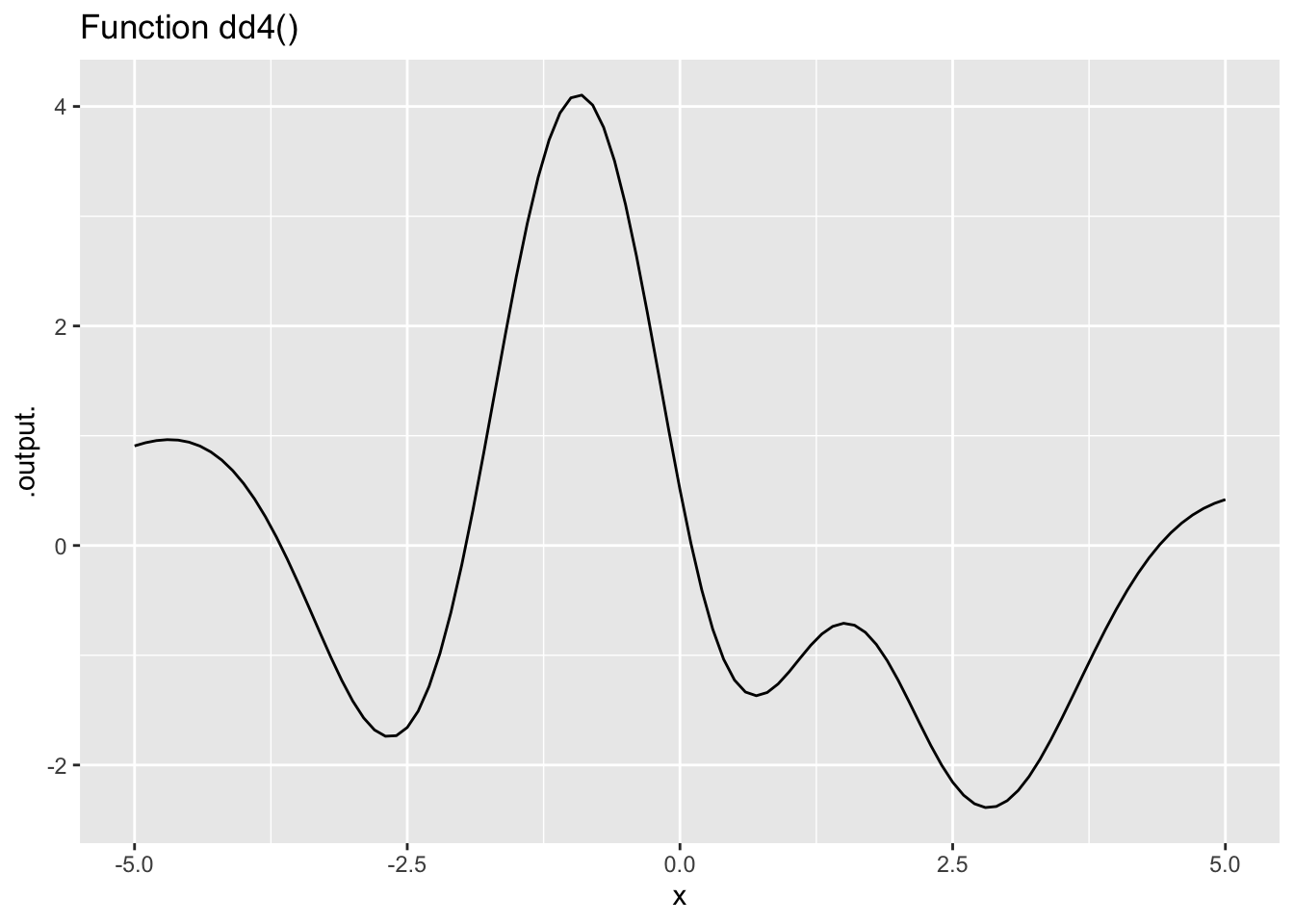
- The second derivative of Function A() is which of the following:
question id: deer-pitch-saw-QA1
- The second derivative of Function B() is which of the following:
question id: deer-pitch-saw-QA2
- The second derivative of Function C() is which of the following:
question id: deer-pitch-saw-QA3
- The second derivative of Function D() is which of the following:
question id: deer-pitch-saw-QA4
Exercise 5
Draw the graph of a function from your imagination over the domain \(-5 \leq x \leq 5\). The function should be continuous everywhere except at \(x = -2, 1, 3\).
Draw the graph of a second function from your imagination over the same domain as in (1). The second function should be continuous everywhere in domain: no discontinuities. It should also have a derivative everywhere except at \(x = -2, 1, 3\).