\(3\vec{a} - 7\vec{b}\)
\(\vec{a} + 2\vec{b}\)
\(-4 \vec{a} + 7 \vec{b}\)
\(- \vec{a} + 4\vec{b}\)
No combination will reach \(\vec{T}\) exactly.
None of the above
question id: srgM-9
Chap 31 Exercises
\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]
Exercise 1 In this exercise, you will check proposed solutions to the target problem. Each question poses one target problem. One of the answers is correct. Use Active R chunk 1 to select the correct answer.
The vectors you will be working with are: \[\vec{a} \equiv \left(\begin{array}{c}1\\2\end{array}\right)\ \ \ \ \vec{b} \equiv \left(\begin{array}{c}1\\1\end{array}\right)\ \ \ \ \vec{c} \equiv \left(\begin{array}{c}1\\-2\end{array}\right)\ \ \ \ \vec{d} \equiv \left(\begin{array}{c}-6\\2\end{array}\right)\ \ \ \ \vec{T} \equiv \left(\begin{array}{c}3\\-1\end{array}\right)\ \ \ \ \]
i. What linear combination of \(\vec{a}\) and \(\vec{b}\) will reach target \(T\)?
ii. What linear combination of \(\vec{b}\) and \(\vec{c}\) will reach target \(T\)?
\(\frac{4}{3}\vec{b} - \frac{5}{3}\vec{c}\)
\(\frac{2}{3}\vec{b} + \frac{7}{3}\vec{c}\)
\(-\frac{7}{3}\vec{b} + \frac{5}{3}\vec{c}\)
\(\frac{5}{3} \vec{b} + \frac{4}{3} \vec{c}\)
No combination will reach $ exactly.
None of the above
question id: srgM-10
iii. What linear combination of \(\vec{b}\) and \(\vec{d}\) will reach target \(T\)?
\(0\vec{b} - \frac{3}{2}\vec{d}\)
\(\frac{1}{2}\vec{b} + \frac{1}{2}\vec{d}\)
\(0 \vec{b} - \frac{1}{2} \vec{d}\)
\(\frac{3}{2}\vec{b} + \frac{1}{2}\vec{d}\)
No combination will reach \(\vec{T}\) exactly.
None of the above
question id: srgM-11
iv. Which of these linear combinations of \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) will reach target \(T\)?
\(\vec{a} -\vec{b} - 2\vec{c}\)
\(2\vec{a} +\vec{b} - 2\vec{c}\)
\(2\vec{a} -\vec{b} + 2\vec{c}\)
\(-2\vec{a} +\vec{b} + 2\vec{c}\)
No combination will reach \(\vec{T}\) exactly.
None of the above
question id: srgM-12
Exercise 2 This exercise uses R to find solutions to the target problem. Each question poses one target problem. You could solve these problems by eye, but we want to get you started on the computer solution so that you will be ready to solve harder problems that must be worked on the computer.
The vectors you will be working with are: \[\vec{a} \equiv \left(\begin{array}{c}1\\2\end{array}\right)\ \ \ \ \vec{b} \equiv \left(\begin{array}{c}1\\1\end{array}\right)\ \ \ \ \vec{c} \equiv \left(\begin{array}{c}1\\-2\end{array}\right)\ \ \ \ \vec{d} \equiv \left(\begin{array}{c}-6\\2\end{array}\right)\ \ \ \ \vec{T} \equiv \left(\begin{array}{c}3\\-1\end{array}\right)\ \ \ \ \]
To make your life easier, here are the commands for defining these vectors. One of the commands is wrong. You will have to correct it before moving on the the rest of the problem.
- What what is the correct linear combination of \(\vec{a}\) and \(\vec{b}\) to reach the target $?
\(-4 \vec{a} + 7 \vec{b}\)
\(-2 \vec{a} + 5 \vec{b}\)
\(2 \vec{a} -7 \vec{b}\)
\(4 \vec{a} - 5 \vec{b}\)
question id: ccmW-1
- What what is the correct linear combination of \(\vec{b}\) and \(\vec{c}\) to reach the target $?
\(\frac{5}{3}\vec{b} + \frac{4}{3} \vec{c}\)
\(\frac{4}{3}\vec{b} + \frac{7}{2} \vec{c}\)
\(\frac{5}{2}\vec{b} + \frac{4}{5} \vec{c}\)
\(\frac{2}{3}\vec{b} + \frac{9}{4} \vec{c}\)
question id: ccmW-2
- What what is the correct linear combination of \(\vec{c}\) and \(\vec{d}\) to reach the target $?
\(\frac{0}{3}\vec{c} + \frac{4}{5} \vec{d}\)
\(\frac{1}{3}\vec{c} + \frac{1}{3} \vec{d}\)
\(\frac{1}{2}\vec{c} + \frac{5}{7} \vec{d}\)
\(\frac{0}{3}\vec{c} + \frac{1}{2} \vec{d}\)
question id: ccmW-3
- What what is the correct linear combination of \(\vec{a}\) and \(\vec{c}\) to reach the target $?
\(\frac{5}{4}\vec{a} + \frac{7}{4} \vec{c}\)
\(\frac{5}{4}\vec{a} + \frac{5}{4} \vec{c}\)
\(\frac{7}{4}\vec{a} + \frac{9}{4} \vec{c}\)
\(\frac{3}{4}\vec{a} + \frac{7}{4} \vec{c}\)
question id: ccmW-4
Activities
Exercise 3 Each of the diagrams below consists of two vectors and a target point (denoted with a bull’s eye). Being a point, the target has a definite location relative to the coordinate axes.
“Solving” this sort of system amounts to finding a linear combination of the two vectors whose result is a vector that can connect the origin to the target. (We call this a target problem.)
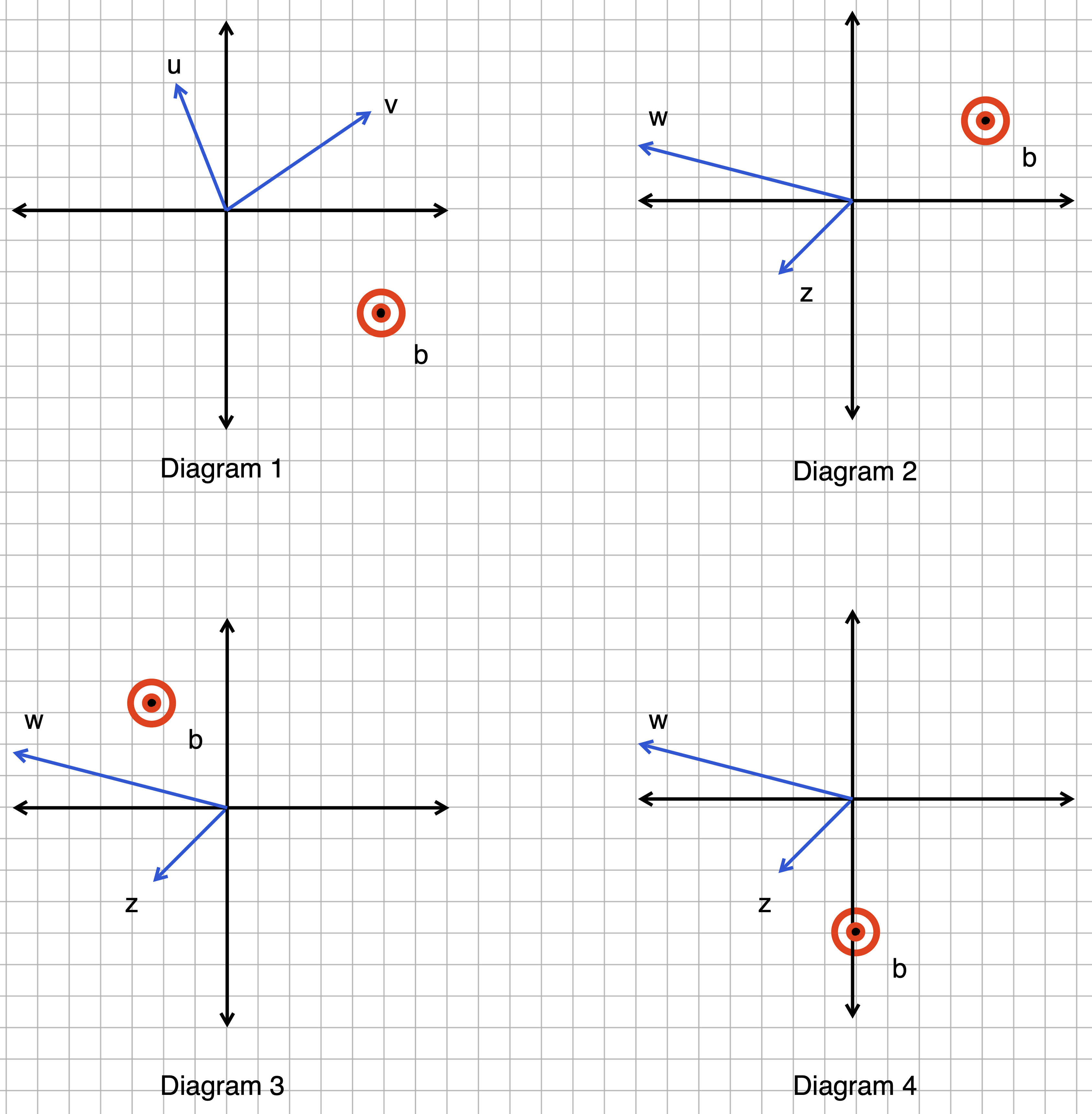
Copy over each diagram to your paper. (Any reasonable approximation will do.) Then, for each diagram, find the linear combination of the two vectors that will reach from the origin to the target. Show your work, meaning that you should draw the scaled vectors in a proper position that demonstrates that they do indeed connect the origin to the target. Underneath the diagram, write down the numerical value of the scalars in the linear combination. (Again, any reasonable approximation will do.)
No answers yet collected