Chap 4 Review

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

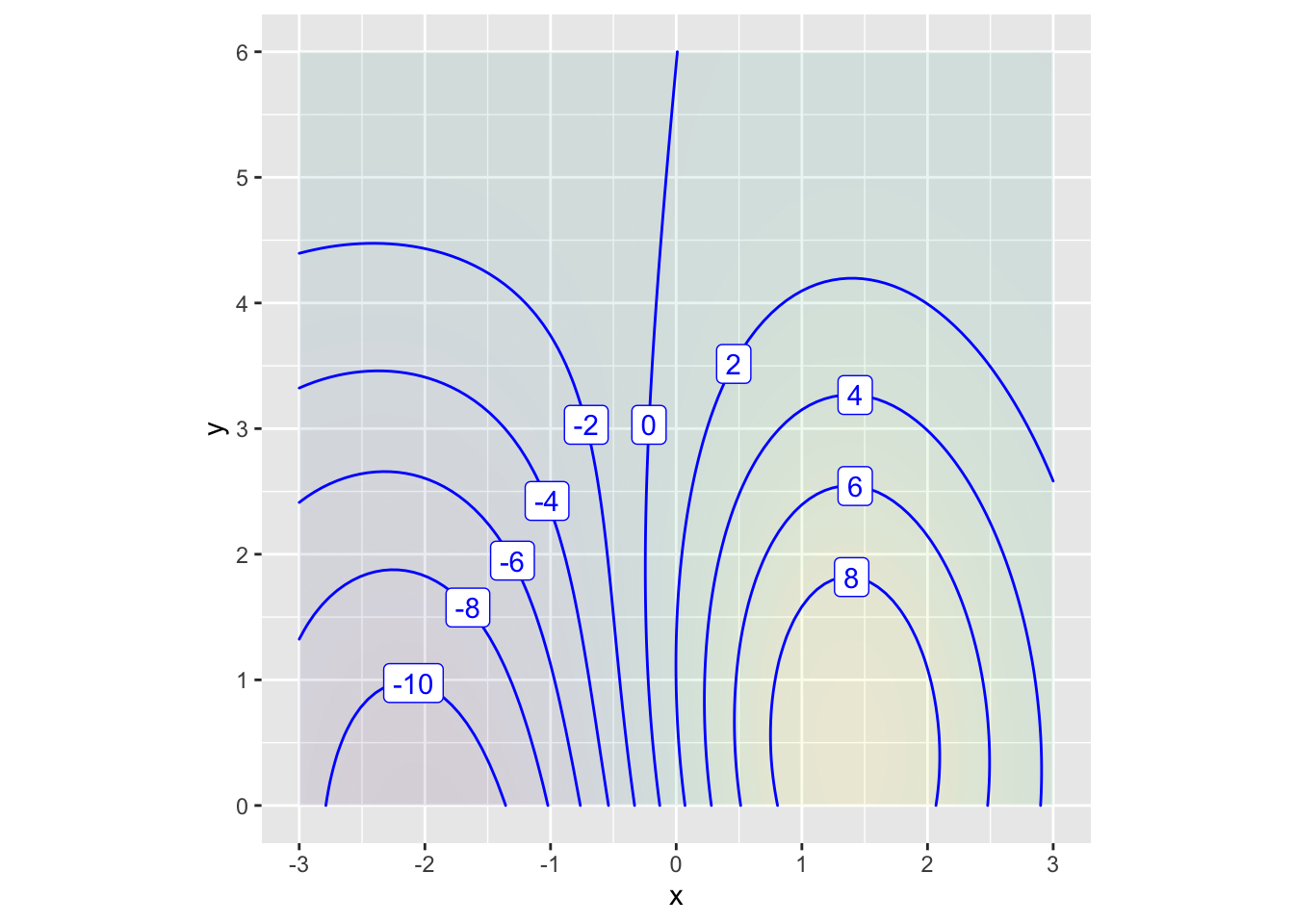
Figure 1: Contour plot of a function for the following three drill exercises.

Exercise 1 Considering the function shown in Figure fig-drill-rev2-05, at which of these inputs is the function output nearly zero?

\((x=0, y=6)\)

\((x=1, y=5)\)

\((x=-2, y=6)\)

\((x=0, y=1)\)

question id: drill-Quiz-2-9

Exercise 2 Considering the function shown in Figure fig-drill-rev2-05, at which of these inputs is the function output nearly 1?

\((x=0, y=6)\)

\((x=1, y=5)\)

\((x=-2, y=6)\)

\((x=0, y=1)\)

question id: drill-Quiz-2-10

Exercise 3 Considering the function shown in Figure fig-drill-rev2-05, at which of these inputs is the function output nearly zero?

\((x=0, y=6)\)

\((x=1, y=5)\)

\((x=-2, y=6)\)

\((x=0, y=1)\)

question id: rX4ZzL

Exercise 4 Which of these is a positive-going zero crossing of \(g(t)\) where \[g(t) \equiv \sin\left(\frac{2\pi}{5}t-3\right)\ ?\]

\(t=15/2\pi\)       \(t = 2 \pi/15\)       \(t = 3\)       None of the above      

question id: drill-Quiz-2-11

Exercise 5 Which of the following is a positive-going zero crossing of \(g(t)\)? \[\sin\left(\frac{2 \pi}{5} (t - 3) \right)\]

\(t=-5\)       \(t=-3\)       \(t=0\)       \(t=3\)       \(t=5\)      

question id: drill-Quiz-2-14

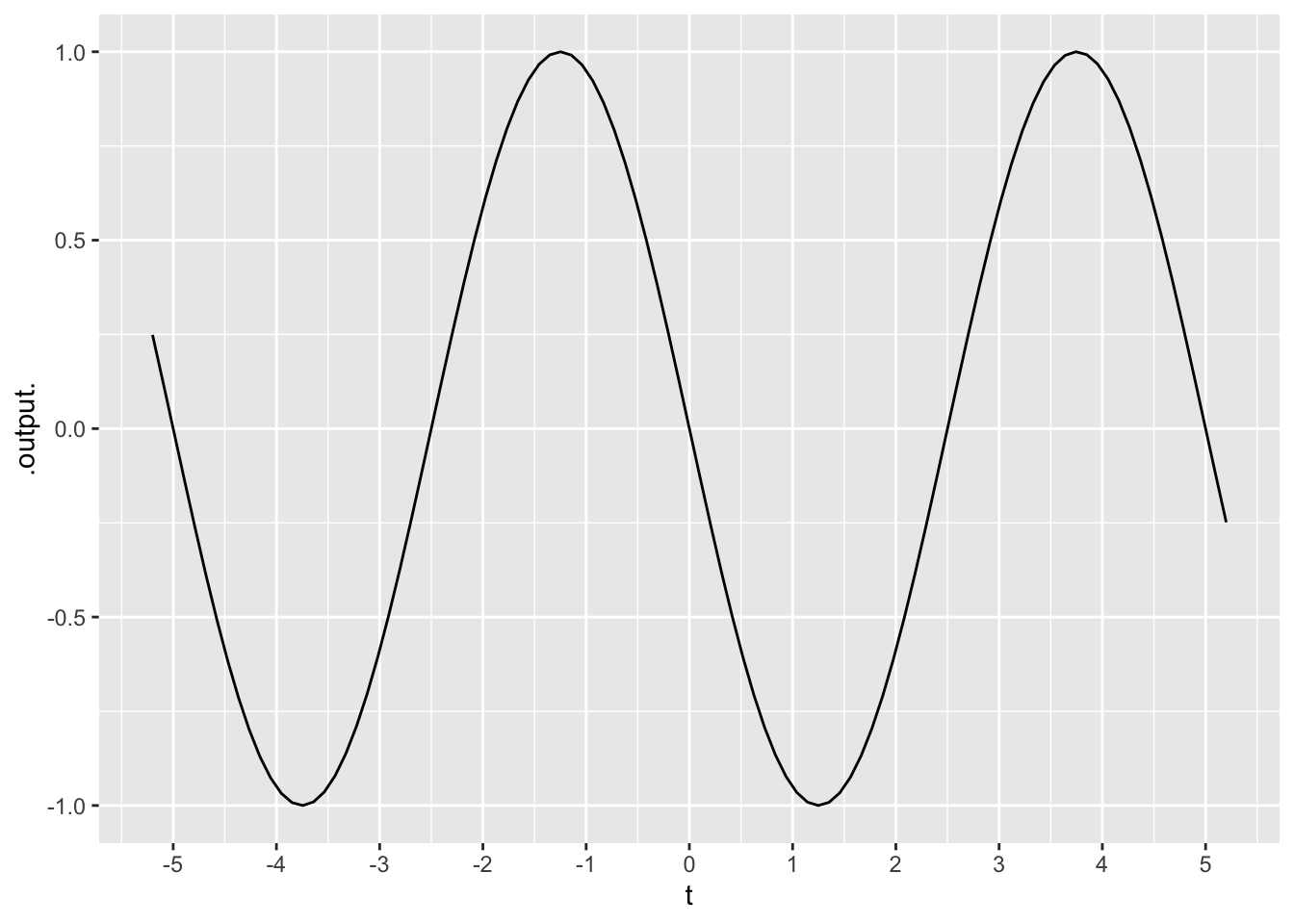
Figure 2: Slice plot of a function for the following drill exercise.

Exercise 6 Which input is a negative-going zero-crossing of the function graphed in Figure fig-rev2-02?

\(t = -2.5\)       \(t = -1.25\)       \(t = 0\)       \(t = 1.25\)       \(t = 2.5\)      

question id: drill-Quiz-2-2

slice_plot(sin(2*pi*t/5) ~ t, domain(t=c(-5.2,5.2))) %>%
  gf_refine(scale_x_continuous(breaks = -5:5))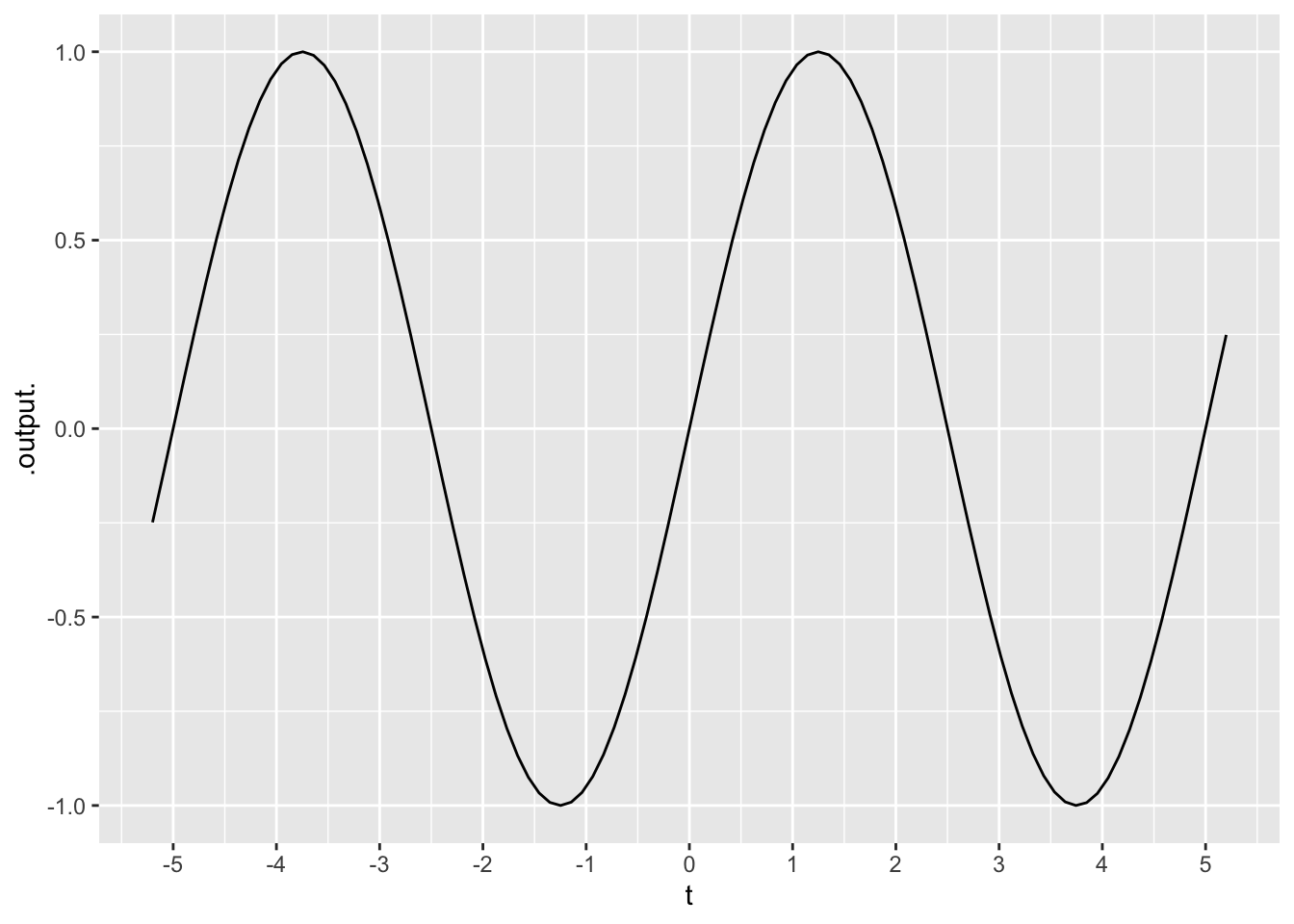

Figure 3: Slice plot of a function for the following drill exercise.

Exercise 7 Which input is a positive-going zero-crossing of the function graphed in Figure fig-rev2-01?

\(t = -5\)       \(t = -2.5\)       \(t = -1.25\)       \(t = 1.25\)       \(t = 2.5\)      

question id: drill-Quiz-2-1

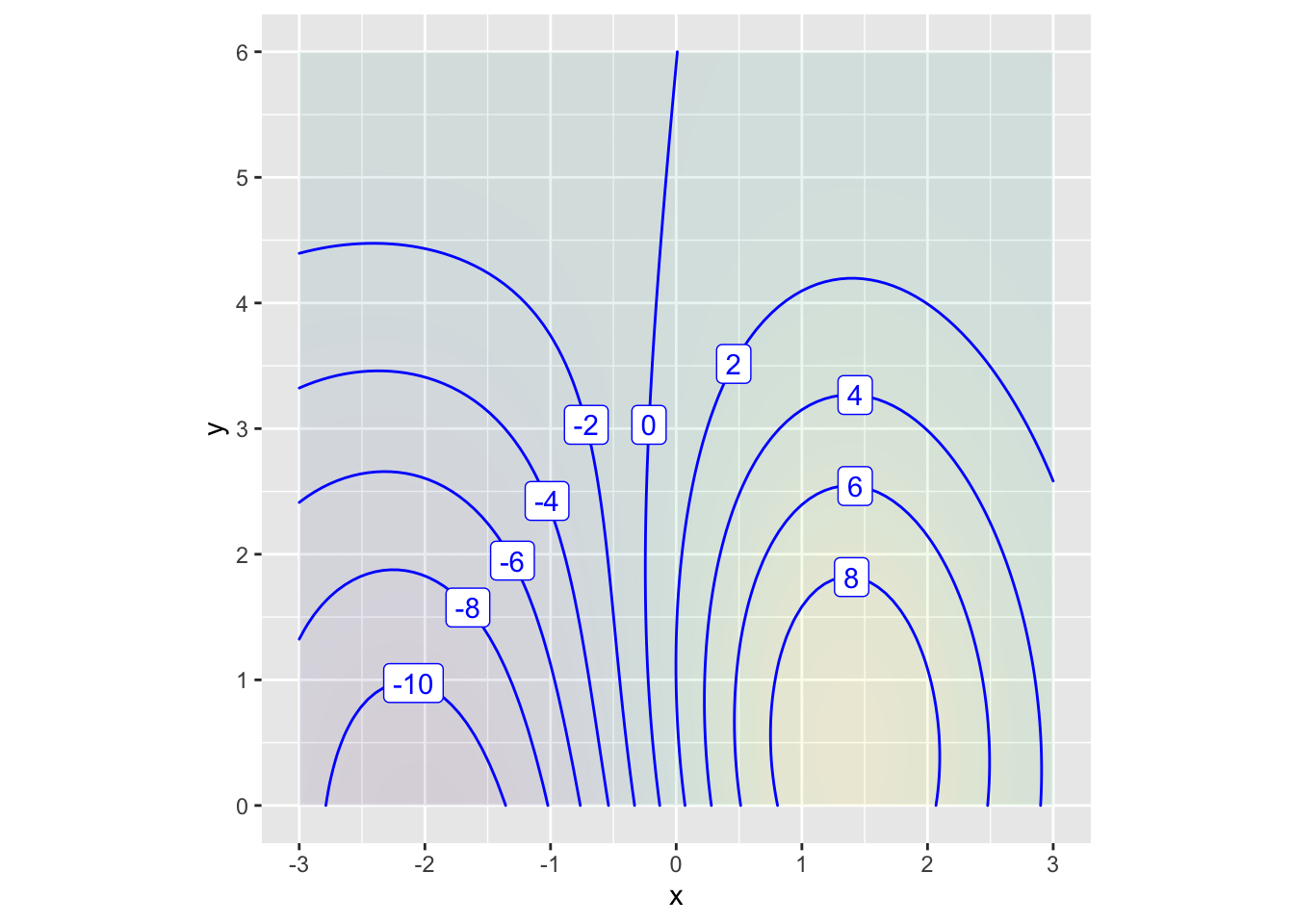
Figure 4: Contour plot of a function for the following three drill exercises.

Exercise 8 Considering the function graphed in Figure fig-drill-rev2-05, at which of these inputs is the function output nearly \(-1\)?

\((x=0, y=6)\)

\((x=1, y=5)\)

\((x=-2, y=6)\)

\((x=0, y=1)\)

question id: drill-Quiz-2-17

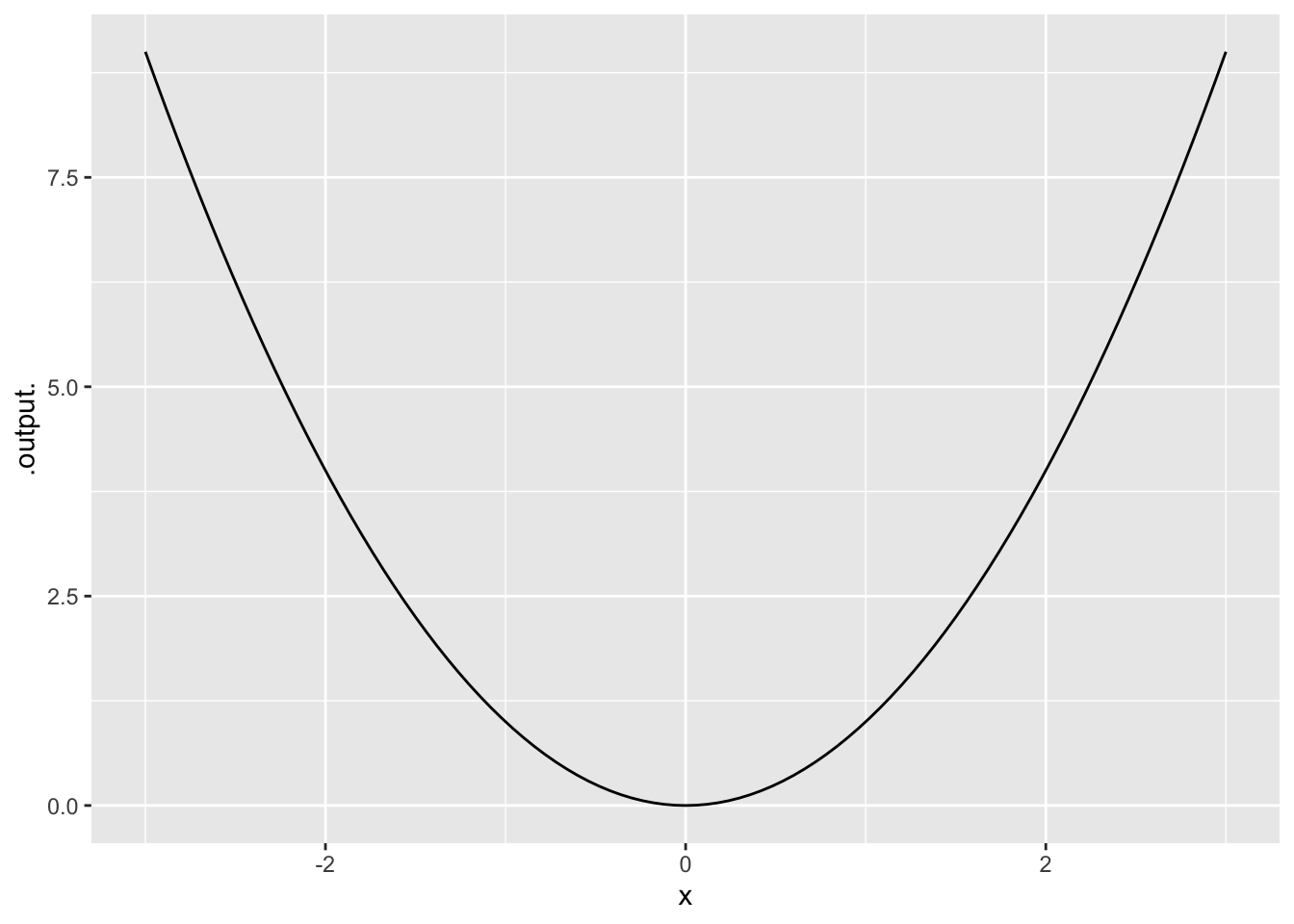
Figure 5: Contour plot of a function for the following drill exercise.

Exercise 9 Which command made this plot in Figure fig-M3-14-05?

slice_plot(x^2 ~ x, domain(x=c(-3,3)))

plot(x^2 ~ x, domain=c(-3,3))

slice_plot(x^2, domain(x=c(-3,3)))

slice_plot(x^2 ~ x, x=c(-3,3))

None of them correspond to the plot.

question id: drill-M04-29

Figure 6: .

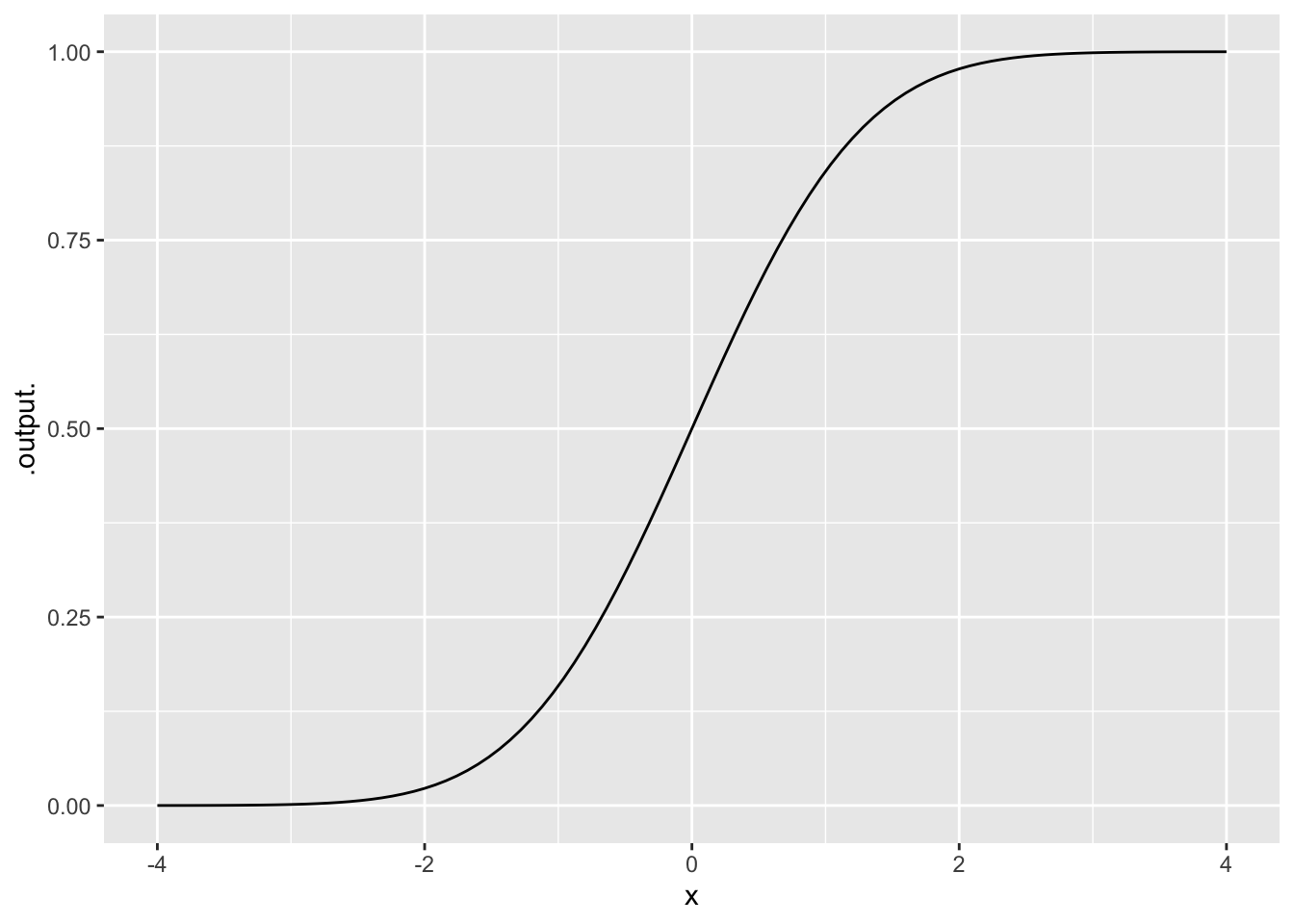
Exercise 10 Which command made the plot in Figure fig-M3-14-04?

slice_plot(pnorm(x) ~ x, domain(x=c(-4, 4)))

slice_plot(pnorm(x) ~ x, domain(x=(-4, 4))

slice_plot(pnorm(x) ~ y, domain(x=c(-4, 4)))

None of them correspond to the plot.

question id: drill-M04-30

Exercise 11 Only one of the following commands will successfully generate the graph of a function. Which one?

slice_plot(exp(y) ~ y, domain(y=c(-4, 4)))

slice_plot(pnorm(x) ~ x, domain(y=c(-4, 4)))

slice_plot(log(x) ~ x, domain(x=c(0; 10)))

slice_plot(dnorm(y)) ~ x, domain(y=c(-3,3)))

question id: drill-M04-31

No answers yet collected