Chap 33 Exercises

$$$$

Exercise 1  

1. What is the name of the with-respect-to input in $\int g(y)dy$?

y

dy

x

t

question id: wolf-beat-book-1

2. What is the name of the with-respect-to input in $\int g(t)dy$

y

dy

x

t

question id: wolf-beat-book-2

3. What is the name of the with-respect-to input in $\int g(x,t)dt$

y

dt

x

t

question id: wolf-beat-book-3

Exercise 2  

1. Which of the following functions is $\int [a+bx]dx$? (Hint: Differentiate each of them until you find the one that matches $a+bx$.)

$ax+\frac{1}{2}b{x}^2+C$

$ax+2b{x}^2+C$

$a+b{x}^2+C$

question id: fir-lead-canoe-1

2. Which of the following functions is $\int e^{-kx}dt$?

$-e^{-kx}/k$

$-k{e}^{-kx}$

$e^{-kx}/k$

question id: fir-lead-canoe-2

Exercise 3 Every function has an anti-derivative. But there are many functions, for example $\text{dnorm}()$ where there is no formula for the anti-derivative. Even so, the R/mosaic antiD() operator will figure out what is the anti-derivative.

For each of the following functions, use makeFun() to implement the function as f(). Then use antiD() to construct the anti-derivative of f() and give this the name F(). Finally, use D() to compute the derivative of F(). Active R chunk 1 is initialized with an example.

Active R chunk 1

1

2

3

4

5

f <- makeFun(x*dnorm(x) ~ x)

F <- antiD(f(x) ~ x)

dF <- D(F(x) ~ x)

slice_plot(f(x) ~ x, bounds(x=0:10)) %>%

  slice_plot(dF(x) ~ x, color="blue", size=3, alpha = 0.2)

1. For the function $f(x)\equiv \text{pnorm}(x^2)$, what is $F(5)$? (Pick the closest answer.)

4

4.5

5

5.5

6

6.5

question id: bee-bid-knife-1

2. For the function $f(x)\equiv \sin (x)\ln (x^2)$, what is $F(5)$? (Pick the closest answer.)

-4

-3.5

-3

-2.5

-2

question id: bee-bid-knife-2

3. For the function $f(x)\equiv x^2\text{pnorm}(x)$, what is $F(5)$? (Pick the closest answer.)

35

37

39

41

43

question id: bee-bid-knife-3

Exercise 4  

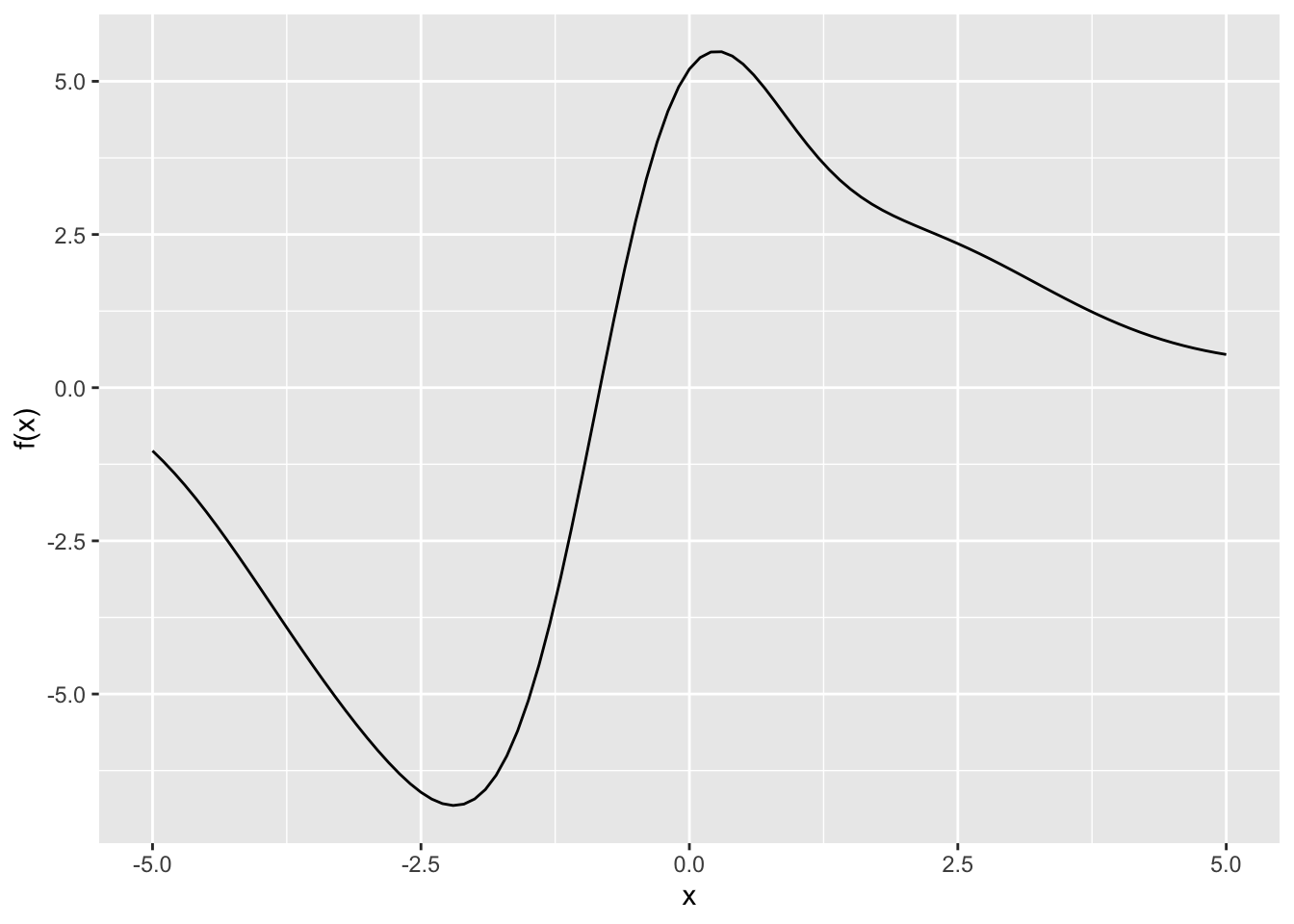
The graph shows a function $f(x)$. Like all functions, it has an anti-derivative.

Active R chunk 2 defines several functions, $F_1(x)$ through $F_4(x)$.

One and only one is the anti-derivative of the function shown in the graph. Which one?

Active R chunk 2

1

2

3

4

F1 <- doodle_fun(~ x, seed = 782)

F2 <- doodle_fun(~ x, seed = 934)

F3 <- doodle_fun(~ x, seed = 297)

F4 <- doodle_fun(~ x, seed = 892)

NOTE: doodle_fun() is a program that generates functions, a different one for each seed. It has been used here to generate F1() through F4() for you to use. Once you run those four lines in Active R chunk 2, you can use slice_plot() in the usual way to plot out any of the four functions over the domain $-5\le x\le 5$.

1. Confirming graphically that a candidate $F_i(x)$ is indeed the anti-derivative of $f(x)$ is hard because the two functions can have very different shapes. But there is a very simple operation you can apply to $F_i(x)$ to make the comparison trivial. What is this operation?

anti-differentiate $F_i(x)$

differentiate $F_i(x)$

compose $f(x)$ with itself

multiply $F_i(x)$ times $f(x)

question id: horse-takes-pillow-1

2. Which one of the functions is an anti-derivative of the function graphed above? (Hint: See the next problem.)

F1()

F2()

F3()

F4()

question id: horse-takes-pillow-2

Exercise 5 What pattern-book function has a derivative $${\partial }_{x}f(x)=\frac{1}{x}?$$

$f(x)\equiv e^x$

$f(x)\equiv sin(x)$

$f(x)\equiv \ln (x)$

$f(x)\equiv \text{dnorm}(x)$

question id: frog-choose-coat-1

What pattern-book function has a derivative $${\partial }_{x}f(x)=\text{dnorm}(x)?$$

$f(x)\equiv pnorm(x)$

$f(x)\equiv -xpnorm(x)$

$f(x)\equiv dnorm(x)$

$f(x)\equiv -xdnorm(x)$

question id: frog-choose-coat-2

Exercise 6  

1. What is the anti-derivative of Force with respect to distance?

Acceleration

Work/Energy

Momentum

Power

question id: kid-show-blanket-1

2. What is the anti-derivative of Velocity with respect to time?

Momentum

Displacement

Power

Acceleration

question id: kid-show-blanket-2

Exercise 7 The output of a function, being a quantity, has dimension and units. Suppose the dimension of the output of a function $v(t)$ is $L/T$, for instance, meters-per-second.

The anti-derivative function $V(t)\equiv \int v(t)dt$ will also have dimension and units.

Recall that in constructing the anti-derivative using the Euler method, we multiply the values of $v(t)$ times some small increment in the input, $h$. Therefore the dimension of the output of $V(t)$ will be $[v(t)][t]$. So if $[v(t)]=L/T$, the dimension $[V(t)][t]=LT/T=L$. Units for such a dimension would be, for instance, meters. This makes sense, since if you accumulate velocity (meters-per-sec) over an interval of time (sec) you end up with the distance travelled (meters).

Suppose you know the acceleration $a(t)$ of an object as a function of time. The dimension of acceleration is $L/T^2$.

1. What is the dimension of $$\int a(t)dt\text{?}$$

$L/T^3$       $L$       $LT$       $L/T$       $L{T}^2$      

question id: units-of-antiD-1

Suppose you know the power consumed by an appliance $p(t)$ as a function of time. Typically appliances have a cycle and use different amounts of power during different parts of the cycle. (Think of a clothes washer.)

2. What will be the dimension of $\int p(t)dt\text{?}$

energy       force       acceleration       length      

question id: units-of-antiD-2

Exercise 8 The following graphic was produced based on data from the US Centers for Disease Control in early December 2020. It shows deaths as a function of time of year.

1. What are the units of the quantity on the vertical axis of the graph?

people/week       people weeks       people       none of these      

question id: ftm1

2. What is the dimension of the quantity on the vertical axis?

T       T${}^{-1}$       L/T       Dimensionless      

question id: ftm2

3. What are the units of the quantity on the horizontal axis?

Unitless       Months       Weeks       Days      

question id: ftm3

Suppose we want to use the information in the plot to estimate the total number of deaths in 2019. This is conceptually an integral of the death rate over the entire year. An integral has units that are the product of the vertical units times the horizontal units. Here, that is people.months/week.

As a shortcut we will model the 2019 death-rate function as a segment of a sine wave:

1

2

3

4

f2019 <- makeFun(60000 - 8000*sin(2*pi*t/24) ~ t)

slice_plot(f2019(t) ~ t, bounds(t=0:12)) %>%

  gf_labs(y = "Deaths per week", x="Month") %>%

  gf_lims(y = c(50000, 80000))

Here’s the integral over the year:

1

2

F2019 <- antiD(f2019(t) ~ t)

F2019(12) - F2019(0)

This is a precise-looking answer, but it is completely wrong. There were approximately 3,000,000 deaths in the US in 2019.

Explain what’s wrong with the estimate based on F2019(12) - F2019(0) and how you can easily fix it. (Hint: What are the units of F2019()?)“)

question id: falcon-tell-mug-essay

Activities

Exercise 9 In the population prediction model at the start of the chapter we want to find a function $P(y)$ that gives the population as a function of year $y$. From the data, we plotted out $\ln [P(y)]$ and found a fairly smooth curve that was upward sloping and concave down. Next, we made a plot of the derivative with respect to year of that upward-sloping, concave-down curve and found the derivative to be well approximated by a straight-line function with a negative slope $a-by$. In other words, we found $${\partial }_y\ln (P(y))=a-by$$ We want to figure out $P(y)$ from this relationship.

Step 1: Anti-differentiate the functions on both sides of the equation. Anti-differentiation has the effect of cancelling out the ${\partial }_y$ from the left side of the equation. Anti-differentiating the right side means calculating $\int [a-by]dy$.

Task 1: Confirm that $\int [a-by]dy=ay-\frac{1}{2}b{y}^2+C$.

Step 2: From Step 1 we have translated the relationship between population and year into this form:

$$\ln (P(y))=ay-\frac{1}{2}b{y}^2+C$$

Task 2: Exponentiate both sides of the newly framed relationship to get $$P(y)=\exp (ay-\frac{1}{2}b{y}^2+C)=e^{ay-b{y}^2}{e}^C=A{e}^{ay-b{y}^2}$$ where $A=e^C$.

Step 3: Let’s declare that $y=0$ means year 2020.

Task 3: Find the census estimate of the population in 2020 and use that information to estimate the parameter $A$ in $P(y)=A{e}^{ay-b{y}^2}$.

Step 4: The per-capita growth rate is $$G(y)\equiv \frac{{\partial }_{y}P(y)}{P(y)}\approx \frac{{\partial }_{y}A{e}^{ay-b{y}^2}}{A{e}^{ay-b{y}^2}}=a-2by$$ The data suggest that the current growth rate is about 1% per year, so $G(0)=a=\approx 0.01$. We also know that the growth rate will be around zero in 2070 years time. Year 2070 corresponds to $y=50$. Consequently, $G(50)=0.01-2\cdot 50\cdot b\approx 0$. You can easily solve this for $b$.

Task 4: You now have numerical estimates for the parameters $A$, $a$, and $b$ in the function $P(y)$. Using these parameters, plot out $P(y)$ for the next 200 years. According to the prediction, what will be the population in year 2220?

1

2

3

4

5

6

7

# Fill in your estimates for A, a, and b.

P <- makeFun(A*exp(a*y - b*(y^2)) ~ y, 

             a = ____, b = ____, A = ____)

# y = 200 is year 2220.

slice_plot(P(y) ~ y, bounds(y=c(0,200)))

# At y=200, the estimate is 50 M

Exercise 10 A textbook might have a problem like this: $$\text{Find}\int x^{2}dx$$ This is a command to you, the student, to find a simpler algebraic form for the function $\int x^{2}dx$. The answer the textbook seeks is, of course, $$\frac{1}{3}{x}^3+C$$.

I would rather textbooks say: “Write an algebraic expression for the anti-derivative of the function $f(x)\equiv x^2$.” We don’t really need the $\int$ involved.

Now consider a textbook problem like this: $$\text{Find}{\int }_{500}^{1000}\frac{x^2}{10000000}dx$$

The 0 and 10 here are the “limits of integration.” (The word “limit” here does not have any connection to the concept of “limits” we studied in defining the derivative of a function.) Maybe it would be better to say, “0 to 10 are the bounds of integration.” The idea is that we will accumulate the quantity $x^2/10000000$ over the interval $500\le x\le 1000$.

To be more concrete, watch the first 30 seconds or so of the following video, which shows a truck laying out traffic cones along a road with a few moments showing the “anti” operation of collecting the cones.

Put yourself on the scene when the construction site is being set up, a first step of which is to mark off the construction zone with traffic cones. That is what the truck is doing at the start of the video.

Suppose the truck is at position $x$ along the road. At that position, there are $f(x)$ cones on the truck. We will call this the “cone stock” on the truck. The function ${\partial }_{x}f(x)$ is the derivative of $f(x)$ with respect to $x$: As the truck drives along the road, that is, as $x$ increases, the truck is unloading its stock of cones. How fast is this unloading? In the video it looks like it is about 1 cone every 33 feet, or let’s say 3 cones per hundred feet. That is, the quantity $f(x)$ is changing at a rate of 3 cones per hundred feet: ${\partial }_{x}f(x)=-0.03$. The derivative function is a constant: the cones are being placed evenly along the road.

Now imagine yourself on another day at another place, at the end of construction. The job of the truck is to pick up the cones. Imagine that the density of cones is described by the function $g(x)$. If we evaluate $g(x)$ at a specific point on the road, we get the density of cones at that point for example 6 cones per 100 feet (0.06 cones/foot). The truck has already picked up some cones and is continuing to do so. Suppose that the contractor or laid out the cones was not very good: they weren’t put down at a regular spacing. Instead, in some spots the cones were put close together: so $g(x)$ is large. In other places the cones are far apart: $g(x)$ is small. The higher is $g(x)$, the more densely the cones are spaced.

As it drives along the road, the truck pick up the cones. Suppose the truck is at mile marker 1.3, equivalent to 6864 feet from marker 0. The truck picks up cones until reaching mile marker 2.4: equivalent to 12,672 feet from marker 0. How many cones did the truck pick up? Easy, it is: $${\int }_{6864}^{12,672}g(x)dx$$ The cone density along the road, $g(x)$, is a function of position. But the accumulation from mile marker 1.3 to marker 2.4 is not a function: it is a number of cones. Note the units: $g(x)$ is cones/foot while $\int g(x)dx$ is simply cones.

Now, we might prefer to keep track of the cone stock as the truck drives along the road. This would simply be a matter of counting the number of cones on the truck at each point $x$ along the road. Of course this number is changing with $x$: the stock is a function of $x$. This stock function is what we are trying to find when we anti-differentiate $g(x)$. If we know $g(x)$—the density of cones along the road—we can figure out $G(x)$.

It is not quite the case that $G(x)$ is the stock on the truck. to know that, we would have to know how many cones were on the truck when it started out. All we know for certain is that the flow of cones onto the truck (with respect to road position $x$) is the derivative of $G(x)$ w.r.t. $x$. That is, the flow onto the truck is ${\partial }_{x}G(x)=g(x)$.

When we know $G(x)$ we don’t exactly know the stock on the truck. But from $G(x)$ we can exactly calculate how many cones the truck accumulated from mile marker 1.3 (6864 ft) to 2.4 (12,762 ft). That accumulated number will be $$G(12672)-G(6864)$$ Back to the textbook problem: $$\text{Find}{\int }_{500}^{1000}\frac{x^2}{10000000}dx$$

In terms of road construction, think of this as the number of cones picked up when driving from position 500 ft to position 1000 ft. Evidently, at the start of the run—that is, at $x=500$, the density of cones is ${500}^2/10000000=0.025$ cones per foot: one cone every 40 feet. At the end of the run—position $x=1000$—the density is 0.1 cones per foot: one cone every 10 feet.

The answer to the textbook problem will be a number of cones. To find that number, we can follow this procedure:

1. Find an anti-derivative of the function $g(x)=\frac{x^2}{10000000}$ This will be $G(x)=\frac{x^3}{30000000}$.
2. Evaluate the anti-derivative at the starting and ending points of the run and subtract: $$G(1000)-G(500)=\frac{{1000}^3}{30000000}-\frac{{500}^3}{30000000}=33.333-4.166=29.166\text{cones}$$

Let’s restate this in terms of some typical quantities involving anti-differentiation:

1. $\int g(x)dx$ is just the function $G(x)$, the anti-derivative of $g(x)$ with respect to $x$. We can find an anti-derivative using any of the techniques we are studying for doing so. But to remind us that we can add a constant to any anti-derivative of $g(x)$ and still have an anti-derivative, we write down $+C$.
2. ${\int }_a^{b}g(x)dx$ is the total accumulation of $g(x)$ over the interval $a\le x\le b$. In terms of our road-cone example, this is the number of cones picked up between road position $x=a$ and position $x=b$. We will calculate this number using the anti-derivative evaluated at each endpoint: $${\int }_a^{b}g(x)dx=G(b)-G(a)$$ We don’t have to worry about the $+C$ in problem (1) because we know the starting point for accumulation. At point $x=a$ we had accumulated no cones yet. There might have been some cones already on the truck (that is the $+C$) but it does not matter because we are looking at the difference in the number or cones on the truck at point $x=a$ and $x=b$, and the already-on-the-truck cones cancel out.
3. ${\int }_a^{y}g(x)dx$ can be confusing. We are used to seeing a constant for the upper bound of integration, but here we have a name. It is easier to see what’s going on if we express ${\int }_a^{y}g(x)dx$ in terms of an anti-derivative function $G(x)$: $${\int }_a^{y}g(x)dx=G(y)-G(a)$$ This will be a function of $y$. There is no need to put in a $+C$ because the $+C$ for the first term will be canceled out when we subtract the $+C$ in the second term.

Form (3) is asking us to keep track of how many cones have been added to the truck since we left point $x=a$ and reached some other point $x=y$. If we plug in $y=b$, Form (3) turns into Form (2), how many cones were collected between positions $a$ and $b$. Form (3) is something like the anti-derivative function. The only difference is that we do not need the $+C$ because whatever it might be, it gets canceled out in the subtraction.

Suppose we are asked to calculate yet another quantity:

4. ${\partial }_y{\int }_a^{y}g(x)dx$, the derivative of form (3) with respect to $y$. Again, think of this in terms of the difference of anti-derivatives: $${\partial }_y{\int }_a^{y}g(x)dx={\partial }_y[G(y)-G(a)]={\partial }_{y}G(y)-{\partial }_{y}G(a)={\partial }_{y}G(y)-0=g(y)$$

The next-to-last step reflects that $G(a)$ is a number of cones, not a function of $y$. The derivative with respect to $y$ of something that is not a function of $y$ is always 0.

${\partial }_y{\int }_a^{y}g(x)dx$ tells us how fast the cones are accumulating on the truck as we drive along the road. In other words, ${\partial }_y{\int }_a^{y}g(x)dx$ has units cones/foot and it is exactly the density of cones (per foot of road) at position $y$, that is, $g(y)$, the density of cones at position $y$.

Note in draft

find-C is an exercise connected to a Shiny app. Re-implement the shiny app using ShinyLive, then include the problem here.

33-exercises.rmarkdown

No answers yet collected