Chap 12 Exercises

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1 Your roommate has challenged you to a chocolate chip cookie bakeoff. Your grandmother has sent you the ingredients for her county-fair award winning recipe, but the baking instructions are missing. You decide to construct a model to help you find the optimal combination of how hot to set the oven \((H)\) and baking time \((T)\). You initially come up with the following model for the yumminess \((Y)\) of the cookies as a function of \(T\) and \(H\):

\[Y(T,H)\equiv Y_0+C_TT+C_HH+C_{TH}TH+C_{TT}T^2+C_{HH}H^2\]

  1. Which of the following is a linear term?
\(Y_0\)       \(C_TT\)       \(C_{TH}TH\)       \(C_{HH}H^2\)      

question id: rhinosaurus-send-car-1

  1. Which coefficient represents the inherent yumminess of cookie dough. That is, dough that has no heat applied to it over no time.
\(Y_0\)       \(C_T\)       \(C_H\)       \(C_{TH}\)       \(C_{TT}\)       \(C_{HH}\)      

question id: rhinosaurus-send-car-2

While making practice batches, you obtain the data in the chart below. You note that increasing the baking time from 10 to 15 minutes accounts for an increase of yumminess score by 1. Similarly, increasing the oven heat from 350° to 425° accounts for an increase of yumminess score by 1. Based on this, when you increase both together, you expect a score increase of 2, but instead observe a score increase of 3.

Cookie yumminess
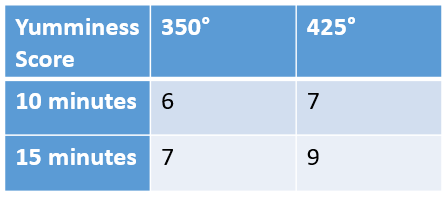
  1. What mathematical behavior is indicated by the data on yumminess?
local max       quadratic relationship       interaction       saddle      

question id: rhinosaurus-send-car-3

  1. What term should be included in your model to capture the behavior in (3)?
\(Y_0\)       \(C_TT\)       \(C_HH\)       \(C_{TH}TH\)       \(C_{TT}T^2\)       \(C_{HH}H^2\)      

question id: rhinosaurus-send-car-4

  1. Given that well baked cookies are more yummy than either raw dough or burnt cookies, what do you infer about the value of \(C_{TT}\)?

\(C_{TT}>0\) (that is \(C_{TT}\) is positive)

\(C_{TT}<0\) (that is \(C_{TT}\) is negative)

\(C_{TT}=0\) (that is the \(T^2\) term does not affect your model)

question id: rhinosaurus-send-car-5

:::

Credit: Math 141Z/142Z 2021-2022 development team

:::

No answers yet collected