f <- antiD( x^1.5 ~ x )
f(5) - f(2)[1] 20.09794Chap 35 Review
\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]
Exercise 1 Using whatever computational tool you like, find the numerical value of this definite integral.
\[\int^{5}_{2} x^{1.5} dx\]
Recall that for a definite integral of function \(f()\), you find the anti-derivative \(F(x) \equiv \int f(x) dx\) and evaluate it at the limits of integration. Here that will be \(F(5) - F(2)\).
Answer
Exercise 2 The following exercises are based on properties of definite integrals that were discussed in class.
Here are some definite integrals for which, without stating anything more about the function, we give you the numerical result.
| \(\int_{2}^{7} f(x) \,dx = -8\) | \(\int_{-6}^{-2} g(x) \,dx = 3\) |
| \(\int_{2}^{12} f(x) \,dx = -14\) | \(\int_{0}^{2} g(x) \,dx = 1\) |
| \(\int_{2}^{7} h(x) \,dx = 5\) | \(\int_{0}^{2} h(x) \,dx = 6\) |
Use the above information to answer the multiple-choice questions below.
- \(\int_{2}^{7} 3f(x) \,dx =\)
-8
-42
-24
13
question id: moose-speaks-greek-1
- \(\int_{7}^{12} f(x) \,dx =\)
6
22
-6
-22
question id: moose-speaks-greek-2
- \(\int_{2}^{7} f(x) + g(x) \,dx =\)
-3
8
-8
insufficient information to answer question
question id: moose-speaks-greek-3
- \(\int_{2}^{2} r(x) \,dx =\)
-3
0
-8
insufficient information to answer question at t
question id: moose-speaks-greek-4
- \(\int_{-6}^{-2} g(x)+3 \,dx =\)
6
15
12
3
question id: moose-speaks-greek-5
- \(\int_{12}^{7} f(x) \,dx =\)
-6
22
6
-22
question id: moose-speaks-greek-6
Exercise 3 Famously, the acceleration due to gravity at the Earth’s surface is a constant: roughly -9.8 meters / sec\(^2\). But let’s write it as a function of time: \[\text{accel}(t) \equiv -9.8\] Galileo climbs up to the top of the Tower of Pisa, 56.7 meters above the ground. He is holding a small lead ball between thumb and forefinger. He spreads his fingers and the ball starts to fall from a standstill. How fast will the ball be going as it falls.
In this problem, we are given information in the form of acceleration, and want to turn it into a statement about velocity. Remembering that acceleration is the derivative of velocity with respect to time, we see this as an anti-derivative problem:
\[\text{vel}(t) \equiv \int \text{accel}(t) dt = \int -9.8 dt = -\int 9.8 dt\] \[\text{vel}(t) = -9.8 t + C\ .\]
- Imagine that the time of release was \(t=3\) seconds. Remembering that 9.8 is in meters/sec\(^2\), what is the value of \(C\) in the velocity function?
29.4 meters per sec\(^2\)
29.4 meters per sec
29.4 meters
29.4 dimensionless/unitless
question id: falling-from-pisa-1
Where will the ball be in 2 seconds after release (that is, at 5 seconds)? “Where” is a position question, so we need to convert the original information that we had in terms of acceleration into information in terms of position.
We’ve already used the relationship between acceleration and velocity (acceleration is \(\partial_t\) accel(t)) to compute the velocity vel(t) at any time: vel(t) \(= -9.8 t + 29.4\) and we know the units of \(t\), \(-9.8\) and \(29.4\).
Since velocity is the derivative of position with respect to time, we can compute position as the anti-derivative of velocity: \[\text{pos}(t) = \int \text{vel}(t) = \int (29.4-9.8 t) dt\] \[\text{pos}(t) = 29.4 t - 9.8 \frac{t^2}{2} + C_{pos}\] Another \(C\)! we are writing it as \(C_{pos}\) to remind us that this \(C\) is different than the \(C\) that appeared in the vel(t) function. That \(C\) was from the accumulation of acceleration to get velocity. This \(C_{pos}\), even though it is the same letter, is something different. Remember that \(C_{pos}\) is a reminder that pos(t) is the accumulation of velocity up until time \(t\), but we haven’t (yet) specified when the accumulation started. To calculate the \(C_{pos}\) for the pos(t) function, we need to consider the problem situation (Galileo in Pisa) and figure out some \(t_0\) for which we know \(pos(t_0)\).
What we know here is that at the release time (\(t=3\) seconds) the ball was at the top of the Tower of Pisa. So dist(3) = 56.7 meters.
- What’s the value of \(C_{pos}\) in the distance function given that dist(3) = 56.7 meters?
\(C = 56.7 - 29.4 \times 3 + 9.8 \times 3^2 / 2 = 12.6\) meters
\(C = -29.4 \times 3 + 9.8 \times 3^2 / 2 = 44.1\) meters
\(C = 56.7\) meters
\(C = 0\) meters
A quantity not in meters.
question id: falling-from-pisa-2
- What is the position of the ball two seconds after release? (The units for each of these is “meters” above the ground.)
\(29.4 \times 2 - 9.8 \times 4/2 + 12.6\)
\(29.4 \times 5 - 9.8 \times 5^2/2 + 12.6\)
\(29.4 - 9.8 \times 5 / 2 + 12.6\)
question id: falling-from-pisa-3
Exercise 4 What’s the numerical value of \[\int_2^5 x^{1.5} dx ?\]
0.58 6.32 20.10 27.29 53.6 107.9 1486.8
question id: dolphin-choose-sofa-1
Exercise 5 What’s the numerical value of \[\int^{10}_{0} \sin( x^2 ) dx ?\]
0.58
6.32
20.1
27.29
53.6
107.9
1486.8
question id: crow-bid-gloves
Exercise 6 Famously, the trajectory of a batted ball has the shape of a parabola. A textbook problem in ball studies—sorry, “ballistics” is the accepted term—asks how long is the trajectory followed by a ball that travels a horizontal distance D and reaches a maximum height H. Knowing these things about the batted ball—parabola, D, H— is enough to write down the formula for the height of the ball when it passes over position \(x\) on the ground: \[y = \frac{4H x (D-x)}{D^2}\]
We didn’t ask you to derive the formula, in part because it is only of theoretical interest and not the actual path of a ball in the sky. Nonetheless as a good modeler you should take it apart a bit. Is it a parabola? Is it dimensionally consistent? (\(x\), \(y\), \(D\), and \(H\) each have dimension L) Does it reach height \(H\) at the maximum? (Where is the argmax? What’s the value of the function at the argmax?)
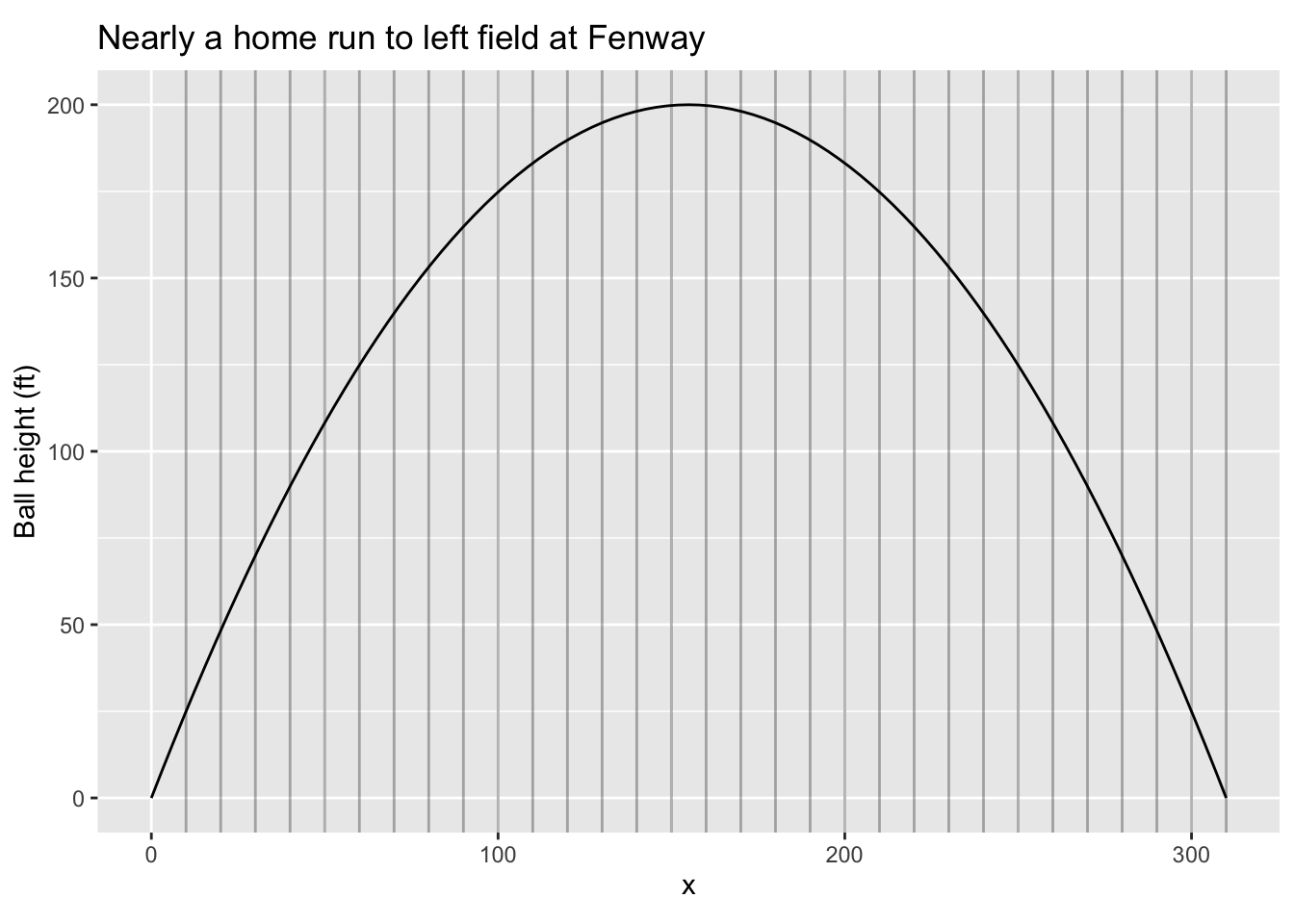
So how long is the trajectory? This is equivalent to asking how long is the piece of string that would cover the graph of the trajectory. To answer this question from the formula, we do the usual thing of breaking up the problem into smaller bits: that is what the vertical gray lines on the graph are doing. The distance between adjacent lines is \(dx\) (10 feet in the graph). Now we ask how long is the trajectory in each segment, then add the results together for all the segments.
Within each segment, the trajectory is very close to being a straight line. The run of the line is \(dx\), the rise is \(y'(x) dx\), where \(y'\) is just a concise way of writing \(\partial_x y(x)\). Using the Pythagorean theorem, the length of the line segment is \(\sqrt( y'^2 dx^2 + dx^2) = \sqrt{y'^2 + 1}dx\).
We can set up the problem algebraically, as we do in this paragraph, or on the computer, as in Active R chunk lst-curve-length. For algebra …Plug in the parabolic formula for \(y\), the length of each little \(ds\) of line segment given \[ds = \sqrt{16 \frac{H^2}{D^4}(D-x)^2 + 1}\cdot dx\] Accumulate the many little \(ds\) segments, we get \[S = \int_{\text{start}}^{\text{finish}} ds = \int_{\text{start}}^{\text{finish}} \sqrt{16 \frac{H^2}{D^4}(D-x)^2 + 1}\cdot dx\\ = \int_{x=0}^{x=D} \sqrt{16 \frac{H^2}{D^4}(D-x)^2 + 1}\cdot dx\] We call this “differential modeling” because we are constructing a model of the segment-length differential as a function of \(x\). Once we have the model, finding the total trajectory length is “just” a matter of calculating the anti-derivative and evaluating it at the endpoints.
It is generally a good idea to check an algebraic solution with a numerical solution. Also, it is a good professional practice to have a way of constructing a simple approximation to the answer. For instance, the trajectory in the graph is very roughly an upside-down V shape. The base of each segment in the V is 155 feet, the height is 200 feet, so the length of the two segments added together is \(2\sqrt{155^2 + 200^2} = 506.1\). We’d expect the length of the actual curve to be a bit longer than this, which it is.
Another approximation of the flight of a baseball corresponds better to what is observed visually:
y <- makeFun(H*sin(pi*(x/D)^2)^(0.5 + x/(2*D)) ~ x, D=310, H=200)Essay: Using Active R chunk lst-curve-length, plot out the new approximation over the domain \(0 \leq x \leq 310\). Home plate is at \(x=0\). Describe briefly what you think might be more realistic about this approximation and what might be less realistic compared to the parabola model.
question id: curve-length-essay
Again using Active R chunk lst-curve-length, compute the length of the curve from \(0.01 \leq x \leq 310\). What is it?
I get an error when I compute DS(0).
528.4 ft
528.7 ft
529.2 ft
529.6 ft
question id: curve-length-1
No answers yet collected