Chap 23 Exercises

$$$$

Loading webR...

Exercise 1 For each of the following, say whether the function is a composition $f(g(x))$ or a product $f(x)g(x)$, or neither.

1. What sort of combination is $h_1(x)\equiv \ln (x)e^x$?

product       composition       neither      

question id: lamb-rise-sofa-1

2. What sort of combination is $h_2(x)\equiv \sin (x)\cos (x)$?

product       composition       neither      

question id: lamb-rise-sofa-2

3. What sort of combination is $h_3(x)\equiv \sin (\ln (x))$?

product       composition       neither      

question id: lamb-rise-sofa-3

4. What sort of combination is $h_4(x)\equiv e^{\ln (x)}$?

product       composition       neither      

question id: lamb-rise-sofa-4

5. What sort of combination is $h_5(x)\equiv \sin (x)-\text{dnorm}(x)$?

product       composition       neither      

question id: lamb-rise-sofa-5

6. What sort of combination is $h_6(x)\equiv e^{x^2}$?

product       composition       neither      

question id: lamb-rise-sofa-6

7. What sort of combination is $h_7(x)\equiv \text{pnorm}(x^2)$?

product       composition       neither      

question id: lamb-rise-sofa-7

8. What sort of combination is $h_8(x)\equiv \text{pnorm}(x)\text{dnorm}(x)$?

product       composition       neither      

question id: lamb-rise-sofa-8

9. What sort of combination is $h_9(x)\equiv 1/\sin (x)$?

product       composition       neither      

question id: lamb-rise-sofa-9

Exercise 2 In function compositions of the form $f(g(x))$, the function $f()$ is called the exterior function and $g()$ is called the interior function.

1. In $\cos (\ln (x))$ which is the interior function?

$\ln ()$       $\cos ()$       $\sin ()$       None of the above       It is not a function composition      

question id: bdb932-1

2. In $1/\sin (x)$ which is the exterior function?

$\text{recip}()$       $\cos ()$       $\sin ()$       None of the above       It is not a function composition      

question id: bdb932-2

3. In $\sin (\frac{2\pi }{P}(t-t_0))$ which is the exterior function?

$t-t_0$       $\frac{2\pi }{P}$       $\frac{2\pi }{P}t$       $\frac{2\pi }{P}(t-t_0)$       $\sin ()$       None of the above       It is not a function composition      

question id: bdb932-3

4. In $\sin (2\pi (t-t_0)/P)$ which is the interior function?

$t-t_0$       $2\pi /P$       $2\pi t/Pt$       $2\pi (t-t_0)/P$       $\sin ()$       None of the above       It is not a function composition.      

question id: bdb932-4

Exercise 3 Recall the differentiation rules for three of the pattern-book functions as presented in [Faulty cross reference: sec-symbolic-differentiation]:

Function name	Formula	Formula for derivative	power-law exponent $p$
Identity	$x$	$1$	1
Square	$x^2$	$2x$	2
Reciprocal	$1/x$	$-1/x^2$	-1

All three of these pattern-book functions are members of the power-law family: $x^p$. They differ only in the value of $p$.

There is a differentiation rule for the power-law family generally. The next question offers several formulas for this rule, only one of which is correct. You can figure out which one by trying the pattern-book functions in the table above and seeing which formula gives the correct answer for the derivative.

Which of these formulas gives the correct differentiation rule for the power-law family $x^p$?

$p{x}^{p-1}$

$(p-1)x^{p+1}$

$x^{p-1}$

$(p-1)x^{p-1}$

question id: doe-pay-kitchen

Exercise 4 Although we created an R function named slopeFun() for the purposes of demonstration, it is better to use the R/mosaic operator D() which calculates the derivative, sometimes using symbolic methods and sometimes using a finite-difference method.

As an example of the use of D(), here is some more R code that defines a function f() and finds ${\partial }_{x}f()$, calling it d_f(). Then each function is plotted on the same domain.

Active R chunk 1

1

2

3

4

5

6

7

8

9

f   <- makeFun(sqrt(exp(x)) - x^2 ~ x)

d_f <- D(f(x) ~ x)

slice_plot(

  f(x) ~ x, 

  domain(x = 0:5))

slice_plot(

  d_f(x) ~ x, 

  domain(x = 0:5), 

  color = "orange3")

For each of the following functions, write a brief comparison of the function to it is differenced version. You can combine phrases such as “same shape”, “different shape. larger in amplitude”, “smaller in amplitude”, “same period”, “shorter period”, “longer period”, or whatever seems appropriate. For instance, for the original example in the sandbox, a reasonable comparison might be, “f() is concave down but Diff(f) is concave up.”

A. For the function $f(x)\equiv 3x$, compare $f()$ to ${\partial }_{x}f$.

B. For the function $f(x)\equiv x^2$, compare $f()$ to ${\partial }_{x}f$.

C. For the function $f(x)\equiv e^x$, compare $f()$ to ${\partial }_{x}f$.

D. For the function $f(x)\equiv e^{-0.3x}$, compare $f()$ to ${\partial }_{x}f$.

E. For the function $f(x)\equiv \sin (x)$, compare $f()$ to ${\partial }_{x}f$.

F. For the function $f(x)\equiv \sin (2\pi x)$, compare $f()$ to ${\partial }_{x}f$).

G. For the function $f(x)\equiv \sin (\frac{2\pi }{20}x)$, compare $f()$ to ${\partial }_{x}f$).

H. The graphic produced by Active R chunk 1 uses two separate frames, one for $f(x)$ and the other for ${\partial }_{x}f(x)$. Explain why in general it’s necessary to plot $f(x)$ and ${\partial }_{x}f(x)$ with different vertical axes. (Hint: Suppose $x$ is denominated in meters or any other dimensionful quantity.)

Exercise 5 MOSAIC Calculus Sec 23.1 explains that in differentiating a linear combination of two functions, or a product of two functions, or one function composed with another, your first task is to identify the two functions $f()$ and $g()$ involved. Second, compute the derivative of each of those functions on its own: ${\partial }_{x}f(x)$ and ${\partial }_{x}g(x)$.

Carry out these two tasks for each of the combined functions shown in the table. (The first row has been done for you as an example.)

Combination	$f()$	$g()$	${\partial }_{x}f()$	${\partial }_{x}g()$
$e^x\ln (x)$	$\ln (x)$	$e^x$	$\text{recip}$ (that is $1/x$)	$e^x$
$sin(e^x)$
$x+x^2$
$1/\sin (x)$
$\text{pnorm}(x{)}^2$
$\sqrt{\text{pnorm}(x)}$
$\text{pnorm}(x^2)$
$\text{pnorm}(\sin (x))$

Exercise 6 Confirm using algebraic manipulation the differentiation rule for a product of three functions:

$${[u\cdot v\cdot w]}^{\prime }=u^{\prime }\cdot v\cdot w+u\cdot v^{\prime }\cdot w+u\cdot v\cdot w^{\prime }$$ Here, $u$ is shorthand for $u(x)$, and $u^{\prime }$ is shorthand for ${\partial }_{x}u(x)$, and similarly for $v$ and $w$.

Hint: $[u\cdot v\cdot w]=u\cdot [v\cdot w]$. So a product of three functions can be seen as a product $u\cdot h$ where $h\equiv v\cdot w$.

Exercise 7 In Exercise 7 you constructed models $D(t)$ of the availability of a drug in the bloodstream for three different pill-taking regimens: every six hours, every eight hours, and a double dose to start followed by a single dose every eight hours. The model for from a single, isolated pill is a zero before the pill is taken, then exponential decay from the level of the pill dose after the pill is taken. Like this:

1

2

3

4

5

pill <- makeFun(

  ifelse(t < 0, 

         0, 

         exp(-k * t)) ~ t, 

  k = log(2)/3)

The parameter $k$ has been set to represent a drug with a half-life of three hours.

The model for the entire regiment is a linear combination of time-shifted single pills, e.g.

1

2

3

4

5

6

regimen8 <- makeFun(

  A*pill(t) + A*pill(t-8) + 

    A*pill(t-16) + A*pill(t-24) + 

    A*pill(t-32) ~ t, 

  A=1

  )

From graphs of the functions themselves it is easy to check whether the availability ever falls below the therapeutic threshold (which we stipulated is 0.25). For instance, the eight-hour regiment with a dose of A=1 does fall below the threshold during the first day. So a larger dose is needed than A=1.

A primary objective in choosing a drug regime is to ensure that the availability stays above the therapeutic level. A secondary objective is to keep the elimination rate small so that the drug can be handled by patients with poorly functioning livers.

The derivative ${\partial }_t\text{regimen8}(t)$ tells the instantaneous rate at which the drug is being administered to and eliminated from the patient’s body. This is the reason for using the name elimination() for the function created in Active R chunk 2.

Active R chunk 2

1

2

3

4

5

elimination <- D(regimen8(t) ~ t)

slice_plot(

  elimination(t) ~ t, 

  domain(t=-1:30)

  )

For each of the three regimens—6-hour, 8-hour, 8-hour-double-first-dose—construct ${\partial }_t\text{regimen}(t)$. Ignoring the glitches due to discontinuity at the times the pills are consumed, which of the three regimens has the lowest average rate of drug elimination?

Exercise 8 The function $F(t)$ shown in Figure 1 is a linear combination of three time-shifted sigmoids.

Figure 1

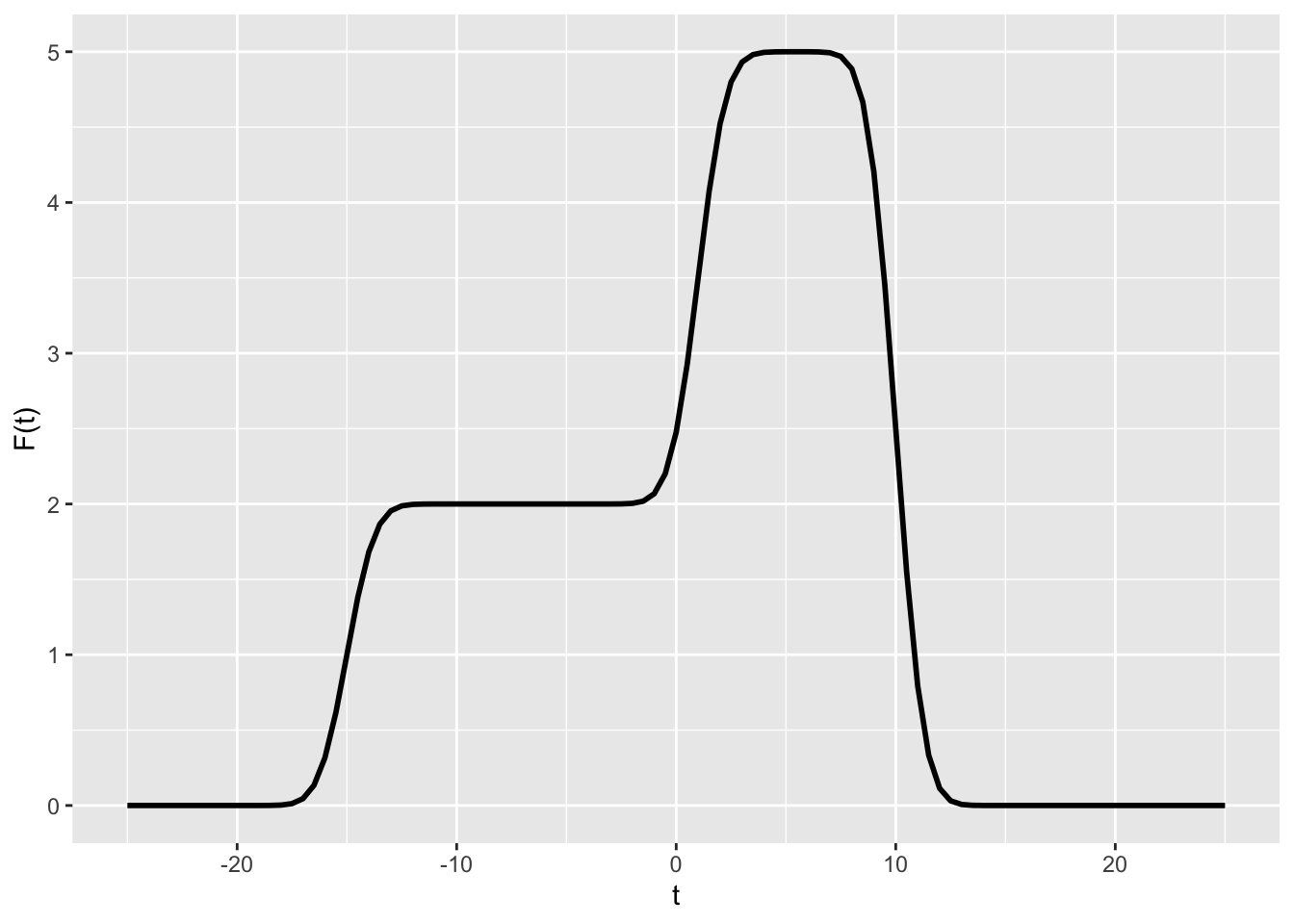
As you know, the derivative of a sigmoid $\text{pnorm}(t)$ is a gaussian with the same center and standard deviation.

1. How many gaussians will be in ${\partial }_{t}F(t)$.

2       3       6       none      

question id: psp4-1

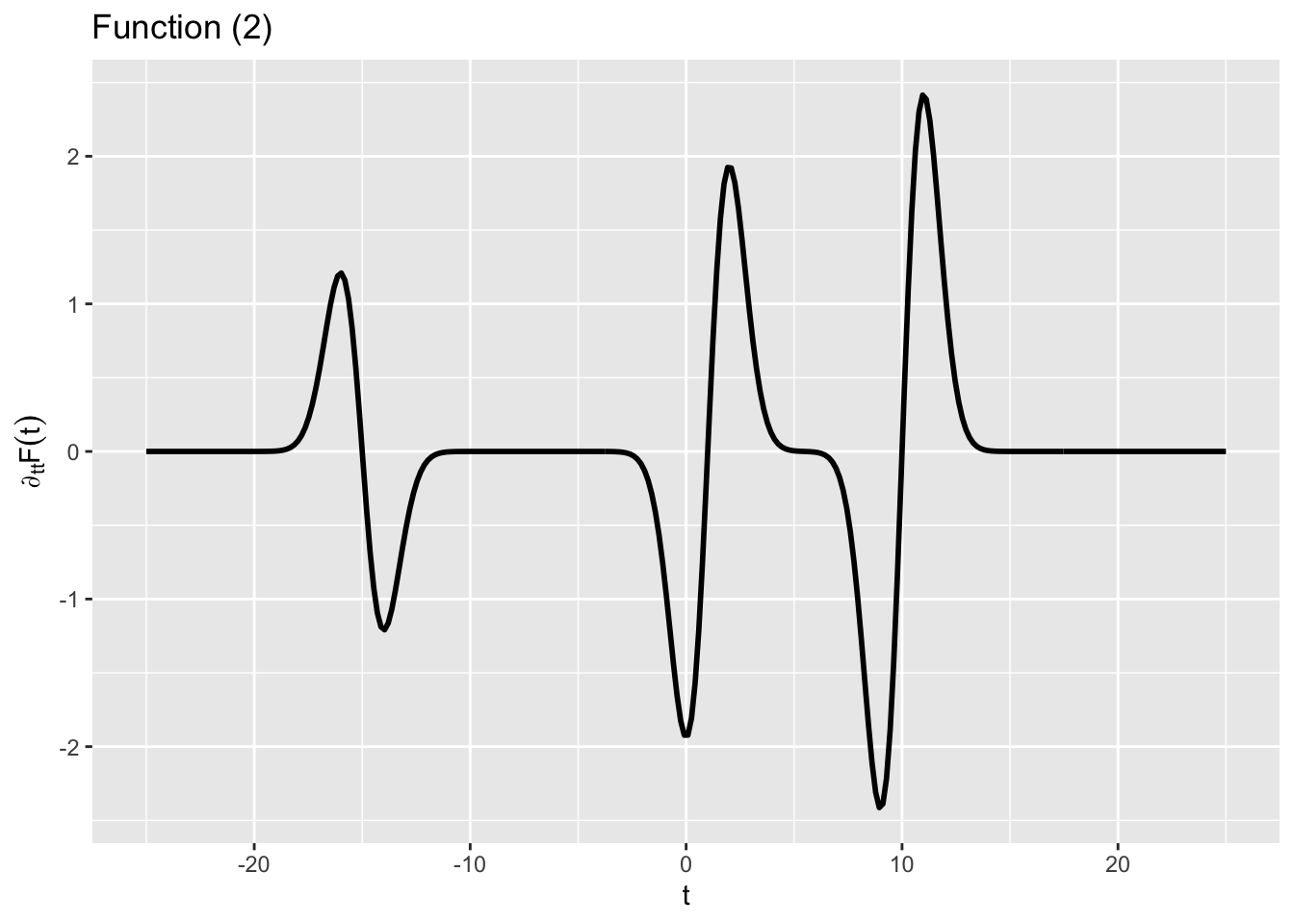
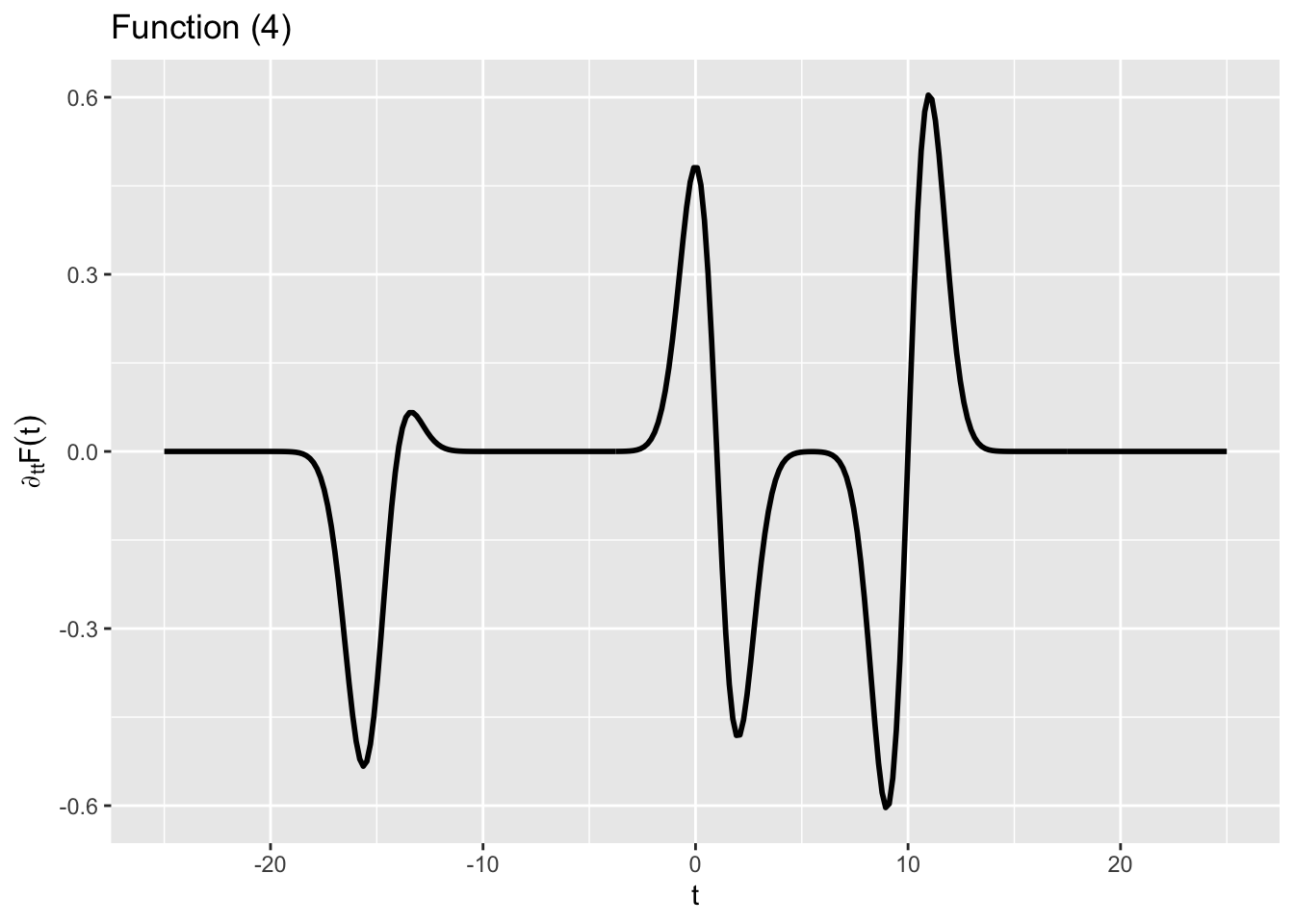
Figure 2 shows several functions. One of them is ${\partial }_{t}F(t)$.

Figure 2

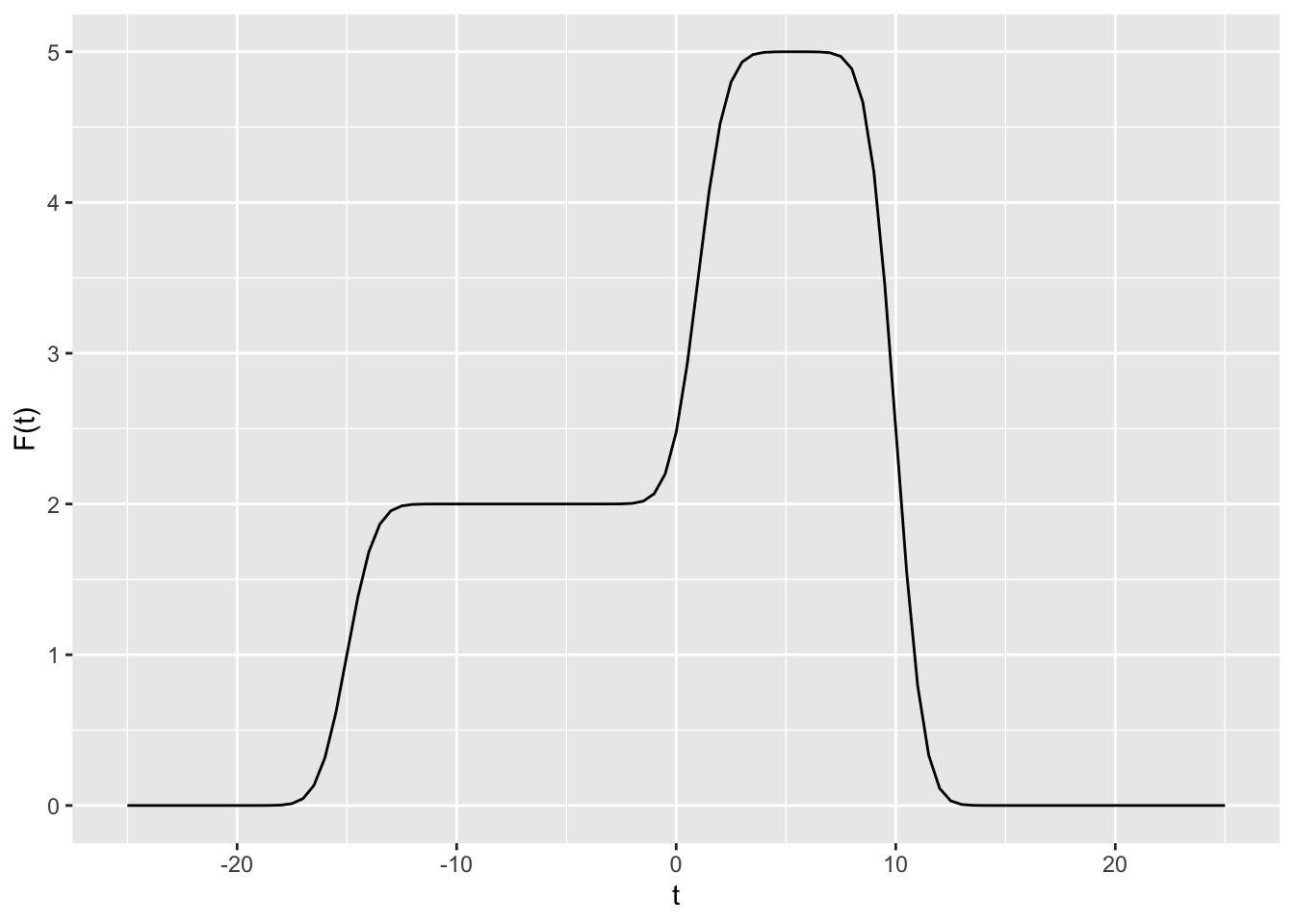
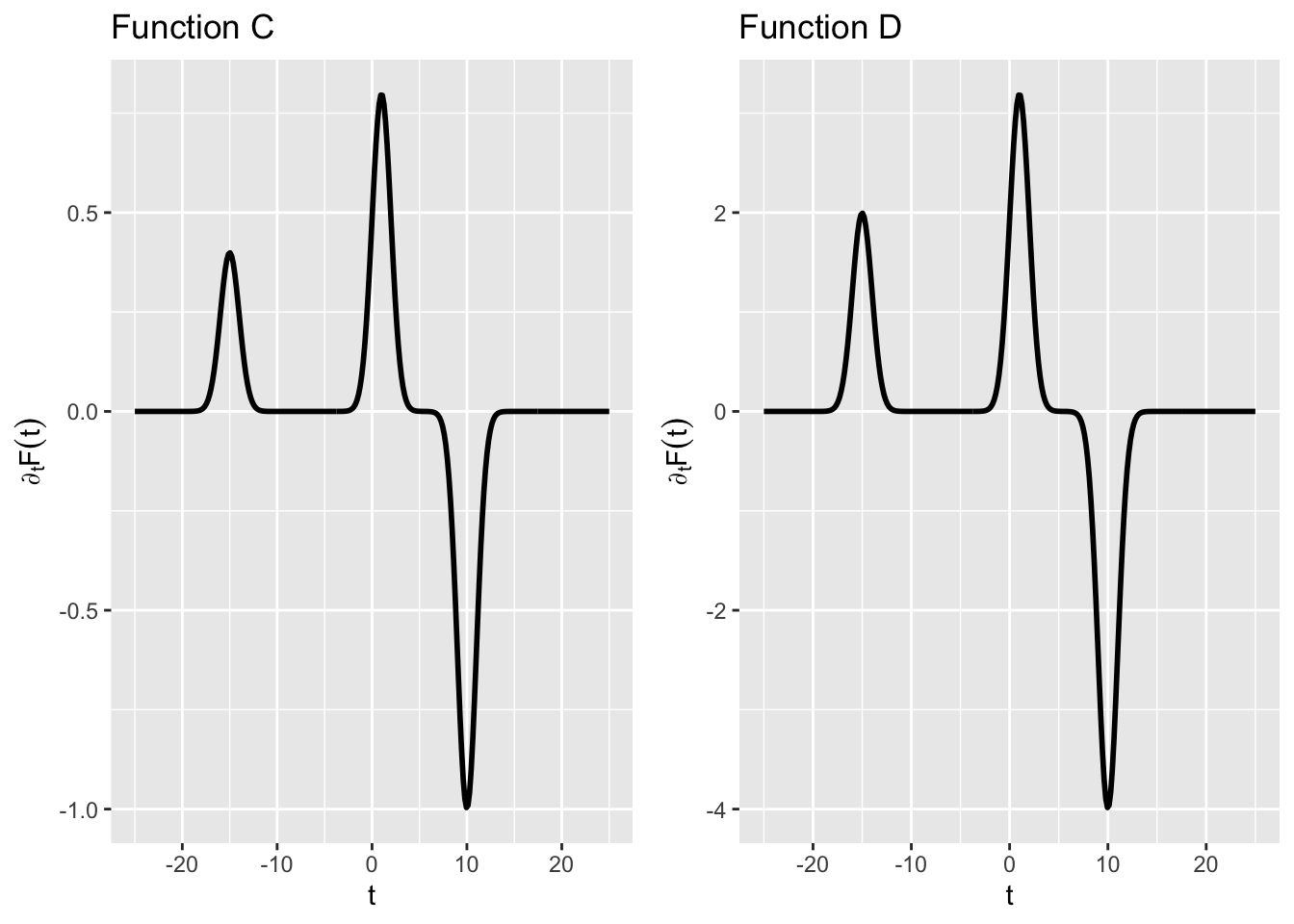
2. Which function is the actual derivative of $F(t)$? (Hint: The vertical axis is important as is the value of $\text{dnorm}(0)$.)

A       B       C       D      

question id: psp4-2

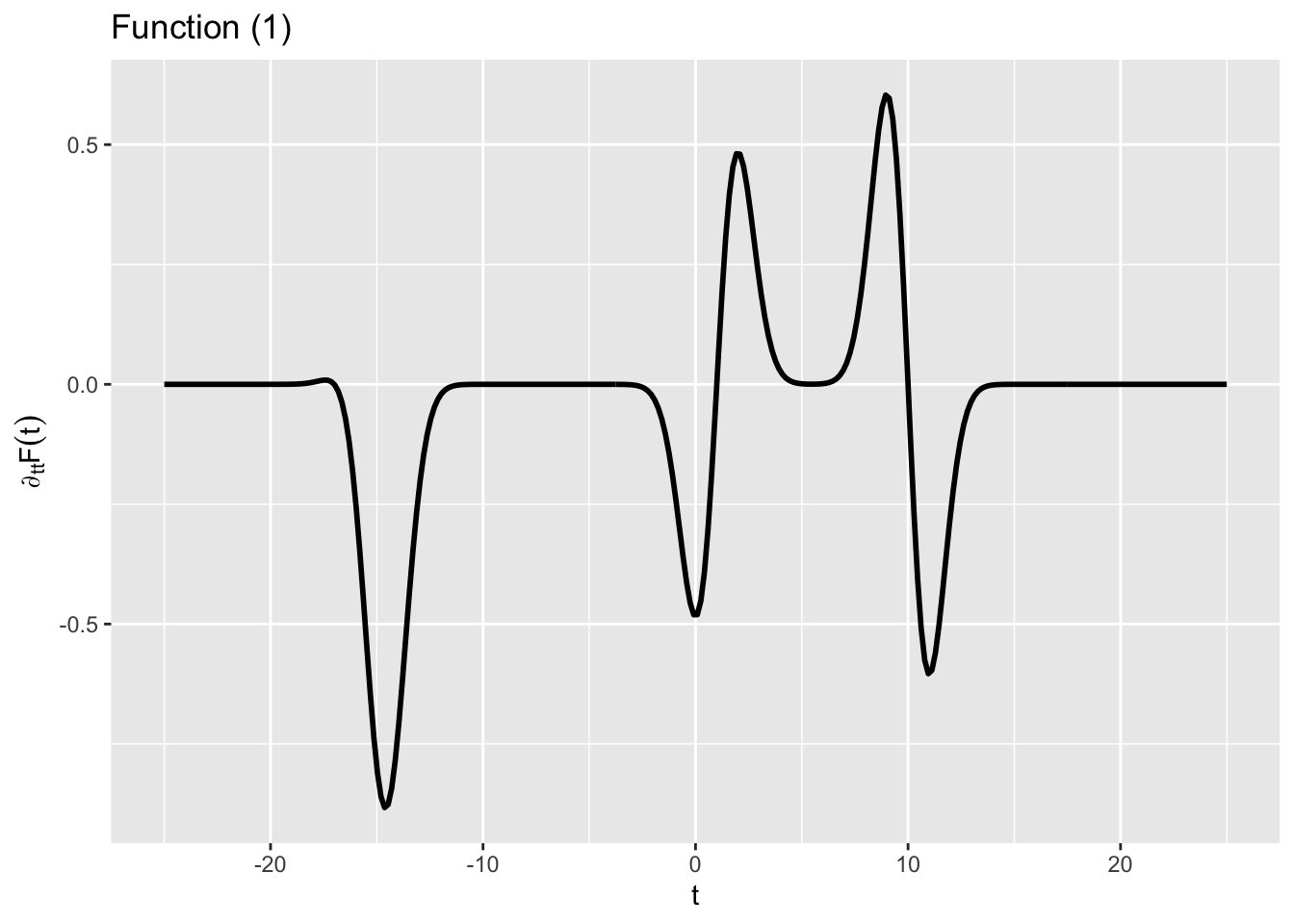
3. Of the functions (1), (2), (3), and (4) below, which function is the second derivative of $F(t)$? (Hints: The vertical axis is important as is the value of $\text{dnorm}(0)$.)

(1)       (2)       (3)       (4)      

question id: pig-see-pantry-3

Figure 3

Exercise 9 Recall from MOSAIC Calculus Sec 6.4 that a function is monotonically increasing on a given domain when the function’s slope is positive everywhere in that domain. A monotonically decreasing function, similarly, has a negative slope everywhere in the domain. When the slope is zero, or positive in some places and negative in others, the function is neither monotonically increasing or decreasing.

Each of the following graphs shows the derivative of some function $f(x)$. (Note: the graph does not show $f(x)$ but rather the function ${\partial }_{x}f(x)$) For each graph, say whether the function $f()$ is monotonically increasing, monotonically decreasing, or neither. (Note that the horizontal scale is the same in every graph, but the vertical scale can be different from one scale to another.)

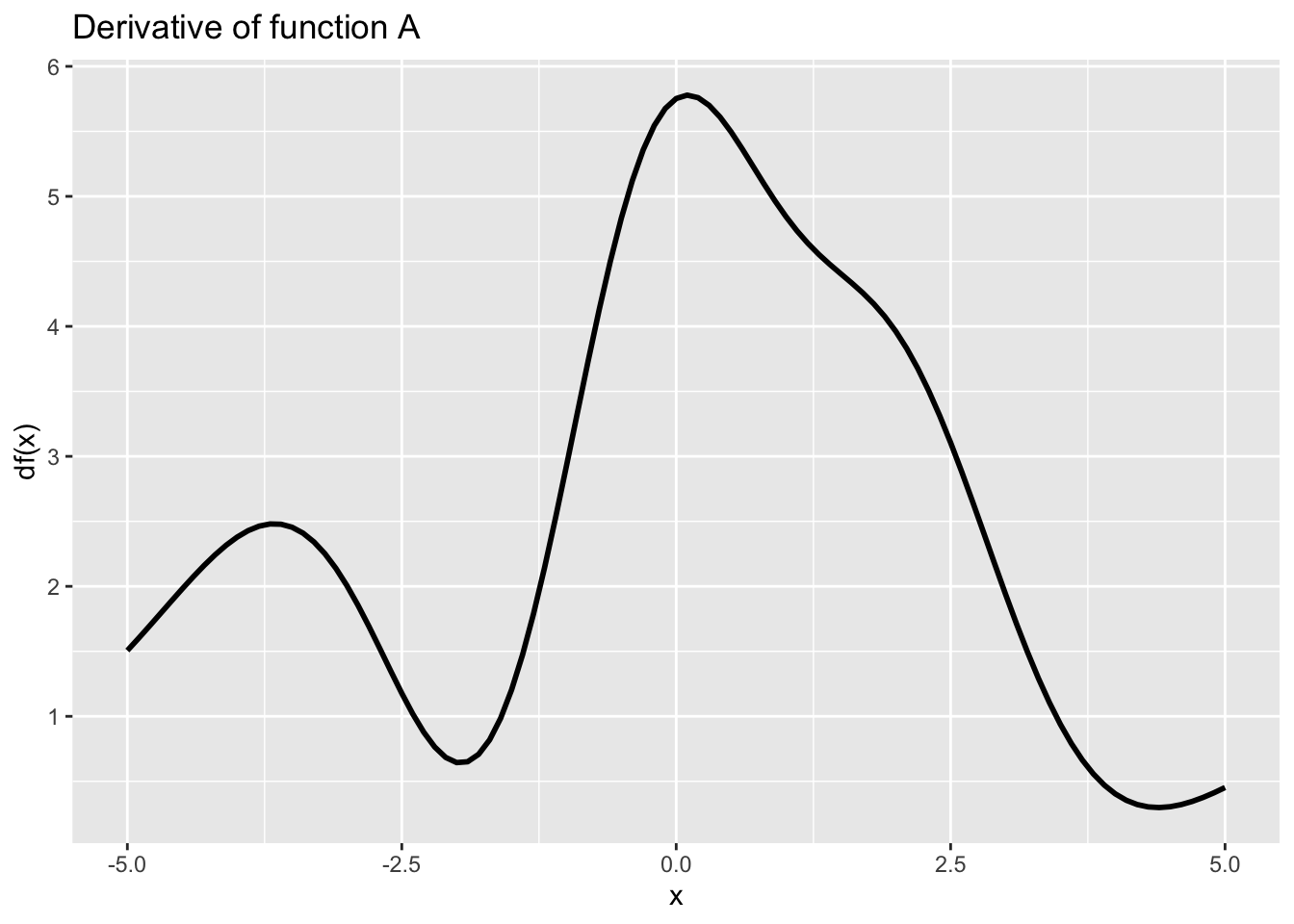
1. Function A is …

monotonically increasing

monotonically decreasing

constant

non-monotonic

Can’t tell from the info provided

question id: pine-lead-car-1

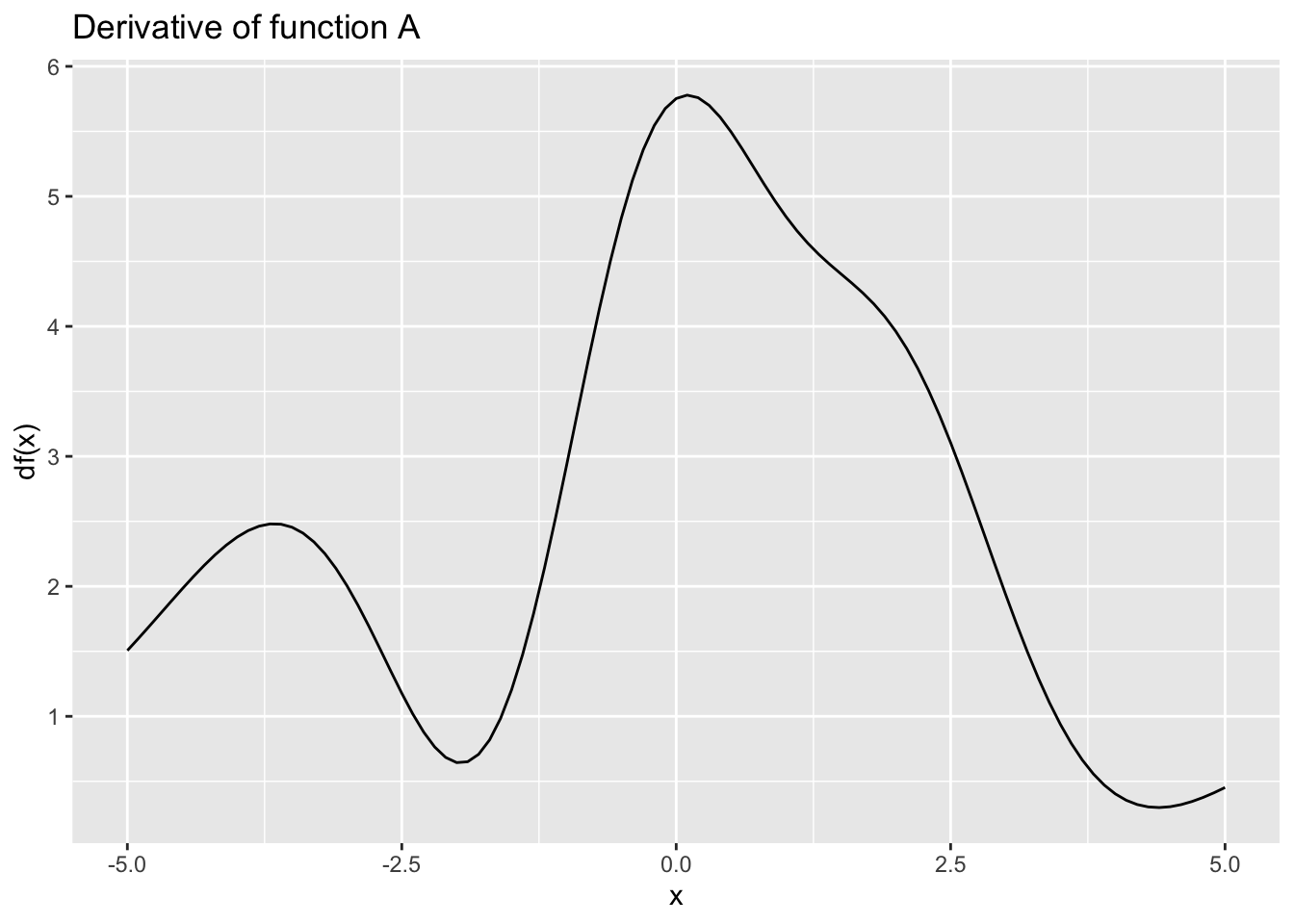
2. Function B is …

monotonically increasing

monotonically decreasing

constant

non-monotonic

Can’t tell from the info provided

question id: pine-lead-car-2

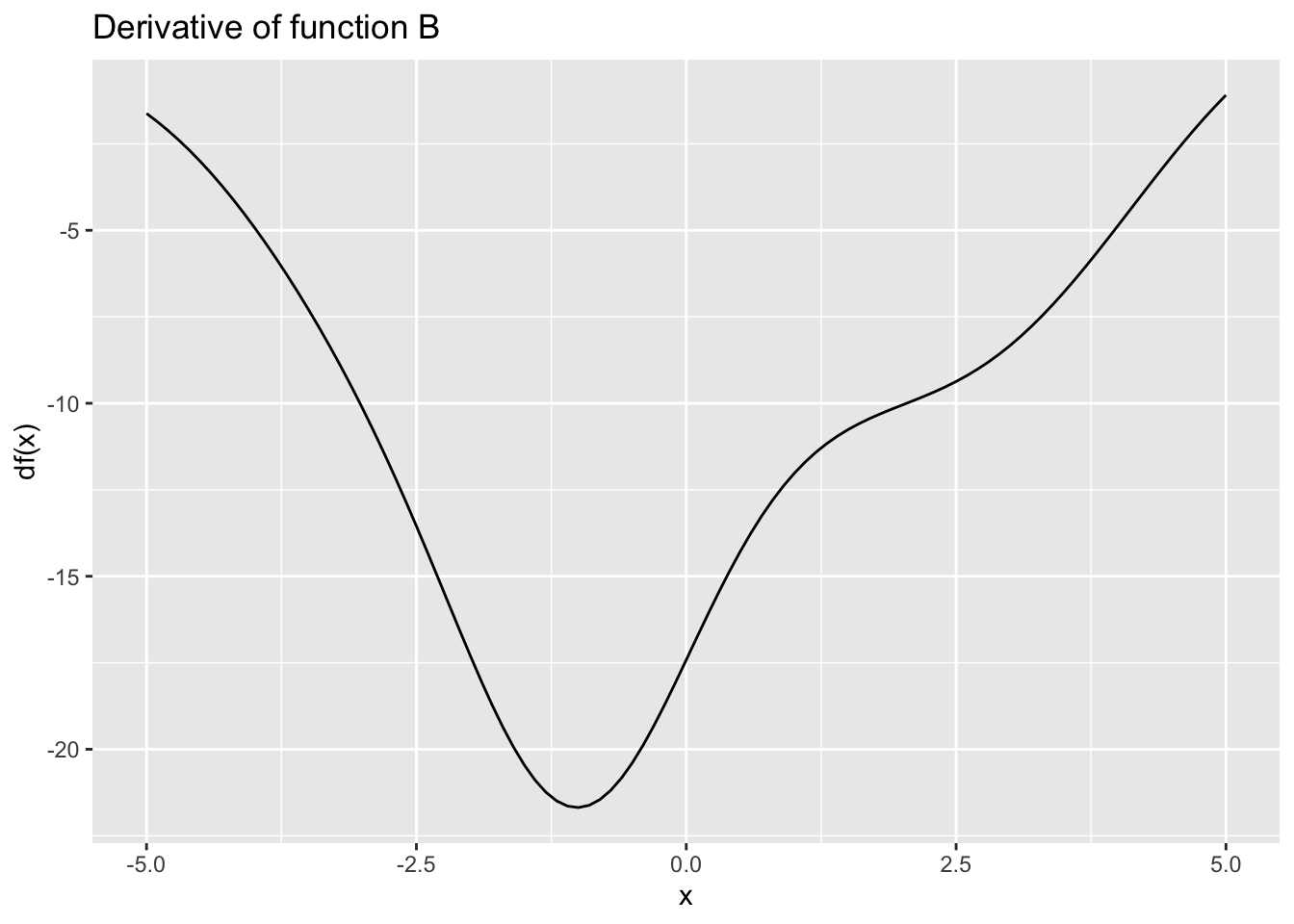
3. Function C is …

monotonically increasing

monotonically decreasing

constant

non-monotonic

Can’t tell from the info provided

question id: pine-lead-car-3

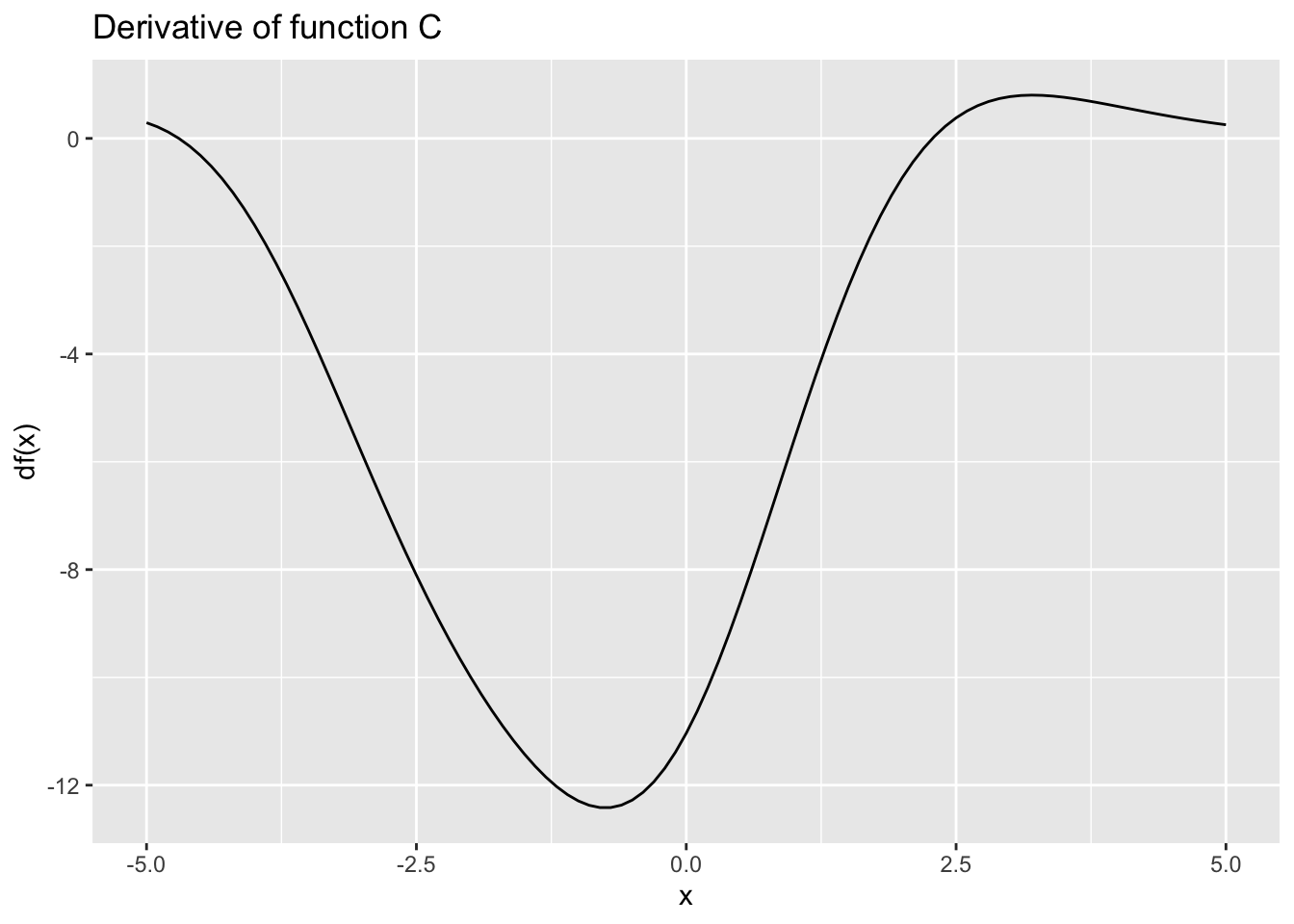
4. Function D is …

monotonically increasing

monotonically decreasing

constant

non-monotonic

Can’t tell from the info provided

question id: pine-lead-car-4

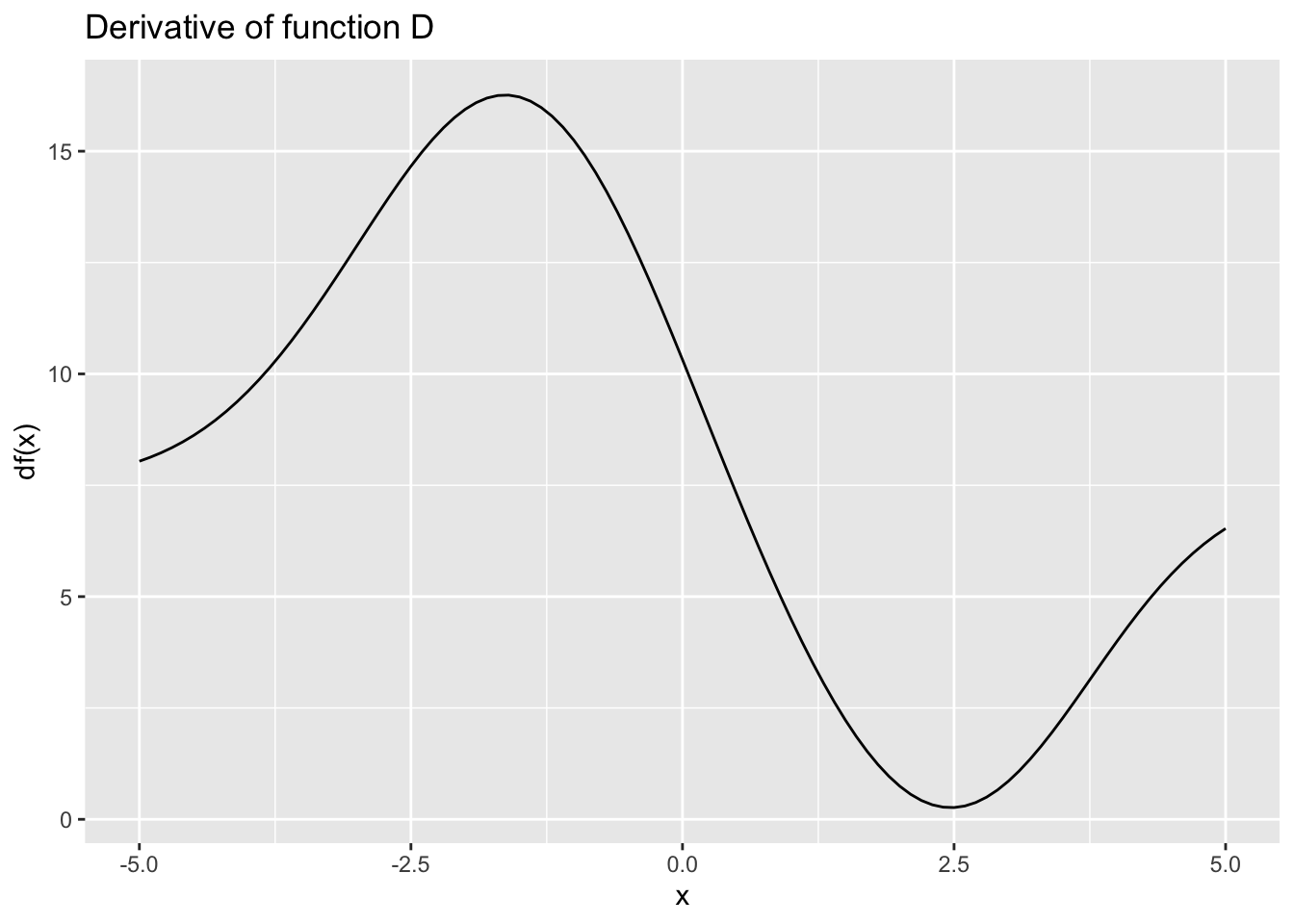
Function E is …

monotonically increasing

monotonically decreasing

constant

non-monotonic

Can’t tell from the info provided

question id: pine-lead-car-5

6. Function F is …

monotonically increasing

monotonically decreasing

constant

non-monotonic

Can’t tell from the info provided

question id: pine-lead-car-6

Activities

Exercise 10  

The chapter gives the simple rule, ${\partial }_x\ln (x)=1/x$. Let’s derive it.

Recall that $\ln (x)$ is defined as the inverse function to $e^x$. That is,

$\ln (e(x))=x$ and $e^{\ln (x)}=x$ (for $x>0$).

Let’s use the first form and differentiate with respect to $x$. We’ll call ${\partial }_y\ln (y)$ by the name $\text{dln}(y)$ and use the chain rule:

$${\partial }_x(\ln (e^x))=\text{dln}(e^x)e^x$$

But remember that $\ln (e^x)=x$, so $${\partial }_x(\ln (e^x))={\partial }_{x}x=1$$

In other words $\text{dln}(e^x)e^x=1$, or, equivalently, $\text{dln}(e^x)=1/e^x$.

This says that the derivative function dln() is such that whatever the input, the output is the reciprocal of the input. We have written the input $e^x$ here, but we might as well have written it $y$. That is

$$\text{dln}(y)={\partial }_y\ln (y)=1/y$$

The name of the input argument is arbitrary, so you might prefer to see the above written as ${\partial }_x\ln (x)=1/x$.

Exercise 11  

Knowing that ${\partial }_x\ln (x)=1/x$ and the chain rule, we are in a position to demonstrate the power-law rule ${\partial }_x{x}^p=p{x}^{p-1}$. The key is to use the identity $e^{\ln (x)}=x$.

$${\partial }_x{x}^p={\partial }_x{\left(e^{\ln (x)}\right)}^p$$ The rules of exponents allow us to recognize $${\left(e^{\ln (x)}\right)}^p=e^{p\ln (x)}$$ Thus, $x^p$ can be seen as a composition of the exponential function onto the logarithm function.

Applying the chain rule to this composition gives $${\partial }_x{e}^{p\ln (x)}=e^{p\ln (x)}{\partial }_x[p\ln (x)]=e^{p\ln (x)}\frac{p}{x}.$$ Of course, we already know that $e^{p\ln (x)}=x^p$, so we have $${\partial }_x{x}^p=x^p\frac{p}{x}=p{x}^{p-1}.$$

Exercise 12 Consider this function, defined piecewise:

$$h(x)\equiv \{\begin{array}{ll}0& \text{for}x<0\\ x^2& \text{otherwise}\end{array}.$$

1. Write the R command to create this function. (Hint: Remember ifelse from [Faulty cross reference: sec-piecewise-intro].)

2. Using Active R chunk 3, plot $h(x)$ over the domain $-1\le x\le 1$, then sketch a copy of the graph on your paper.

Active R chunk 3

1

3. Create the function ${\partial }_{x}h(x)$ by differentiating separately each piece of the piecewise function $h()$. Write down ${\partial }_{x}h(x)$ using mathematical notation similar to the definition of $h(x)$ given above.

4. Sketch a graph of ${\partial }_{x}h(x)$ over the domain $-1\le x\le 1$. You’re welcome to use a Active R chunk 3, but you may be able to figure out the shape of the graph yourself.

5. The shape of the function you sketched in (4) has a name, given in the text in Section @ref(continuity). What is that name?

Now you will do much the same as in items (3), (4), and (5), but instead of the first derivative ${\partial }_{x}h(x)$, create, sketch, and name the second derivative ${\partial }_{xx}h(x)$.

6. Create and write down ${\partial }_{xx}h(x)$ in mathematical notation.

7. Sketch ${\partial }_{xx}h(x)$

8. Classify the smoothness of $h(x)$ using the following table:

Smoothness	Criterion
$C^0$	${\partial }_{x}h(x)$ is discontinuous
$C^1$	${\partial }_{x}h(x)$ is continuous
$C^2$	${\partial }_{xx}h(x)$ is continuous
$C^3$	${\partial }_{xxx}h(x)$ is continuous
$⋮$	and so on.
$C^{\mathrm{\infty }}$	All orders of derivative of $h(x)$ are continous.

Exercise 13 Recall from Exercise 5 the Lorenz curve used to describe income inequality. The Lorenz curve shows the fraction of total income versus population fraction.

Figure 4: A Lorenz curve (blue) fitted to income data from the US in 2009. (See Figure 2.)

Since the population is arranged from poorest to richest along the horizontal axis, Lorenz curves must be both monotonically increasing and concave up. That is, any Lorenz function $L(P)$, where $P$ is the population fraction, must satisfy these criteria:

1. $L(0)=0$
2. $L(1)=1$ that is, the aggregate fraction of income earned by the entire population is 100%.
3. ${\partial }_{P}L(P)>0$ that is, monotonically increasing
4. ${\partial }_{PP}L(P)>0$ that is, concave up.

Consider a function $H(P)\equiv L_1(L_2(P))$ which is the composition of two Lorenz curves.

• A. Use the composition rule to show that $H(P)$ is monotonically increasing. (Hint, calculate ${\partial }_{P}H(P)$ and show that it must be positive.)
• B. Using both the composition and product rules, calculate ${\partial }_{PP}H(P)$ and show that $H(P)$ must be concave up.

Exercise 14 The formula for the function $\text{dnorm}(x)$ is $$\text{dnorm}(x)\equiv \frac{1}{\sqrt{2\pi }}\exp \left(\frac{x^2}{2}\right).$$

A. Use the chain rule to find ${\partial }_x\text{dnorm}(x)$.

B. Confirm from your answer to (1) that there is another formula for ${\partial }_x\text{dnorm}(x)$, namely $${\partial }_x\text{dnorm}(x)=-x\text{dnorm}(x).$$

C. Use the product rule to find ${\partial }_{xx}\text{dnorm}(x)$.

D. From your answer to (3), compute the 3rd derivative ${\partial }_{xxx}\text{dnorm}(x)$:

E. Let’s generalize the pattern. Each of the previous derivatives has been a polynomial—let’s call it $p_n(x)$ for the $n$th derivative—times $\text{dnorm}(x)$. Knowing $p_n(x)$, we can easily find $p_{n+1}(x)$: $$p_{n+1}(x)=-x{p}_n(x)+{\partial }_x{p}_n(x)$$ We know $p_1(x)=-x$ so $p_2(x)=x^2-1$. In turn, this tells us $p_3(x)=3x-x^3$. Find:

1. $p_4(x)$
2. $p_5(x)$
3. $p_6(x)$

Exercise 15 The natural logarithm function, $\ln (x)$, is one of our basic modeling functions. As you know, there are other logarithmic functions. The one most often used is the logarithm-base-10, written ${\log }_{10}(x)$ or log10(x). Ten is an integer, and a nice number to use in arithmetic. So in practice, it is sensible to use ${\log }_{10}()$. (Indeed, ${\log }_{10}()$ is the digit() function, introduced in MOSAIC Calculus Chap 14.

The “natural” in the “natural logarithm” means something different.

The base of the natural logarithm is the number called Euler’s constant and written $e$. As a celebrity number, $e$ is right up there with $\pi$ and $i$. Just as $\pi$ has a decimal expansion that is infinitely long (the familiar $\pi =3.14159265358979...$), Euler’s constant has an infinitely long decimal representation: $e=2.71828182845905...$

It is not obvious why $e=2.71828182845905...$ should be called “natural” by mathematicians. The reasons are:

1. $\ln (x)$ is the inverse of $e^x$, which is special for being invariant under differentiation: ${\partial }_x{e}^x=e^x$.
2. The derivative ${\partial }_x\ln (x)$ which has a particularly simple form, namely, $1/x$.

Let’s look at the log-base-10 and its computer-savvy cousin log-base-2. The very definition of logarithms means that both 10 and 2 can be written $$10=e^{\ln (10)}\text{and}2=e^{\ln (2)}$$ This implies that the base-10 and base-2 exponential functions can be written in terms of Euler’s constant $e$:

$${10}^x={\left[e^{\ln (10)}\right]}^x=e^{\ln (10)x}\text{and}{2}^x={\left[e^{\ln (2)}\right]}^x=e^{\ln (2)x}$$ Calculating ${\partial }_x{10}^x$ or ${\partial }_x{2}^x$ is a matter of applying the chain rule. Use the chain rule to calculate

1. ${\partial }_x{10}^x$
2. ${\partial }_x{2}^x$

Answer

$${\partial }_x[{10}^x]={\partial }_x[e^{\ln (10)x}]=e^{\ln (10)x}\times \ln (10)={10}^x\times 2.3026$$ and $${\partial }_x[2^x]={\partial }_x[e^{\ln (2)x}]=e^{\ln (2)x}\times \ln (2)=2^x\times 0.6931$$

Like $e^x$, the derivatives of ${10}^x$ and $2^x$ are proportional to themselves. For $e^x$ the constant of proportionality is 1, a very natural number indeed.

23-exercises.rmarkdown

No answers yet collected