Black/Dotted
Red/Dashed & Dotted
Blue/Long Dashed
Magenta/Solid
question id: fish-go-scarf-1
Chap 34 Exercises
\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]
Exercise 1 Here is a graph of four different functions.
Regard those four functions as \(F_1(x)\) through \(F_4(x)\).
For each of the following plots, the single function graphed has an anti-derivative which is one of \(F_1(x)\) through \(F_4(x)\). You’re job is to say which is which.
A. Which of the four functions shown in the top graph is an anti-derivative of the function graphed just below?
B. Which of the four functions shown in the top graph is an anti-derivative of the function graphed just below?
Black/Dotted
Red/Dashed & Dotted
Blue/Long Dashed
Magenta/Solid
question id: fish-go-scarf-2
Activities
Exercise 2 The graph shows a continuous function \(G()\) broken up into discontinuous segments.
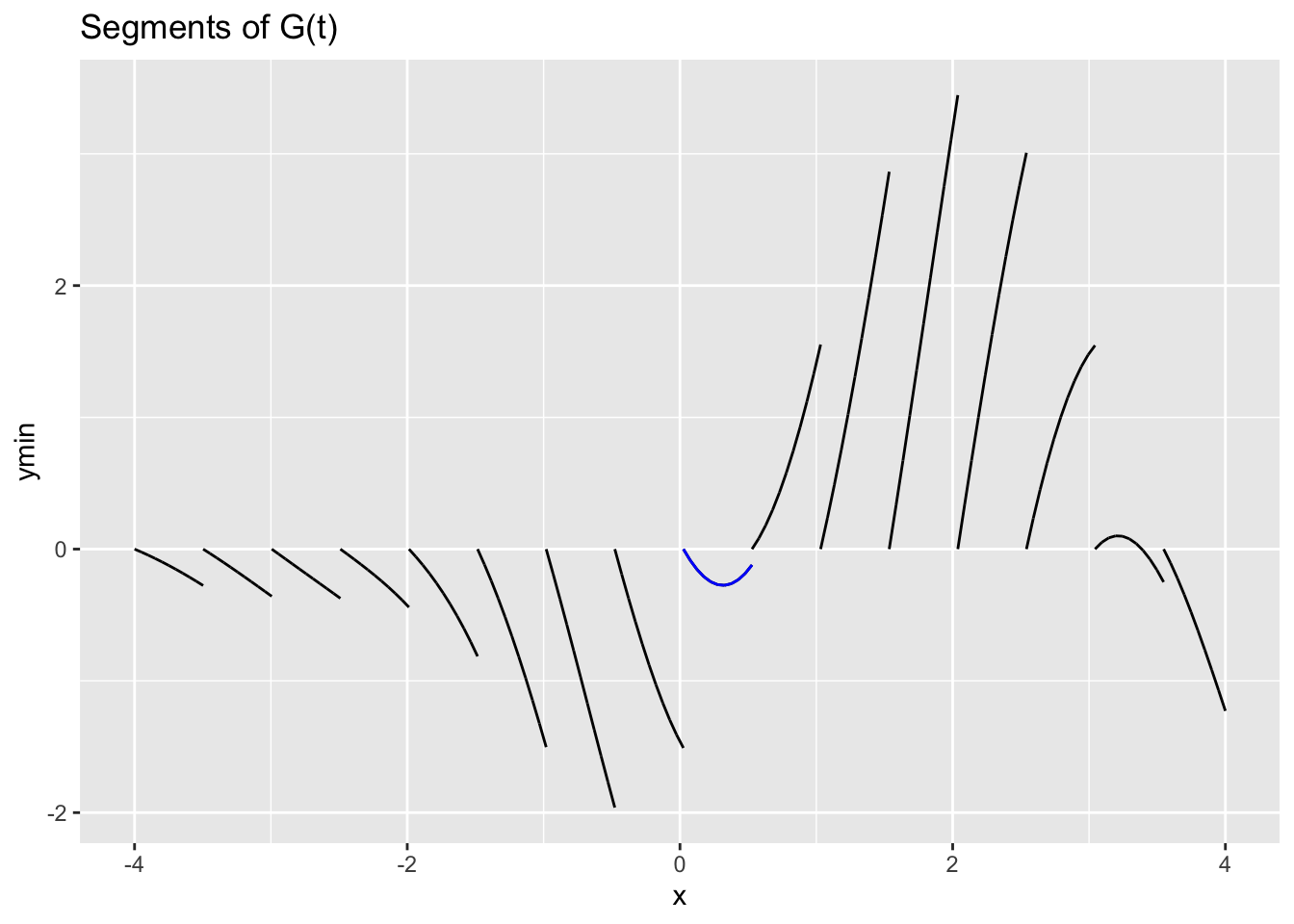
Draw a continuous version of \(G(t)\) by putting together the segments.
Exercise 3 Early in Math 141Z we undertook to figure out how fast a satellite travels. As you recall, we measured the orbit height r from the center of the Earth. Assuming a circular orbit (which is not necessarily a good assumption) the total path length of an orbit is \(2 \pi r\). We also assumed that the acceleration of the satellite due to gravity is 9.8 m/s^2 , the value on the Earth’s surface. (And a reasonably good approximation to the value at a height of, say, 100 mi above the surface.)
Then we asked, how large is the centripetal acceleration needed to keep a satellite in orbit of radius \(r\) at velocity \(v\). We used dimensional analysis to say that \(a = v^2/r\), a formula that is dimensionally consistent. Knowing that \(a \approx 9.8\) m/s^2 , and specifying \(r = 4050mi\) (that is, 100 mi above the surface of the Earth), we solved for \(v\): \[v = \sqrt{a \times r} = \sqrt{9.8 \text{m}\, \text{s}^{-2} \times 4050 \text{mi}} = 191.5 \sqrt{\text{m}\cdot\text{mi}\strut}\ \text{s}^{-1}\]
- What is the numerical value of \(\sqrt{\text{m}\cdot\text{mi}\strut}\) expressed in miles?
\(\sqrt{1609.34 \text{m}^2} = 40.12 m\)
\(\sqrt{40.12 \text{mi}^2} \approx 6.33 \text{mi}\)
\(\sqrt{0.000621371 \text{mi}^2} \approx 0.025 \text{mi}\)
It is crazy to take the square root of a length. There is no such thing as \(\sqrt{1 m\strut}\).
question id: differential-orbit-1
Units aside, consider the formula \(a = v^2/r\). It is dimensionally consistent, but how do we know that acceleration isn’t twice or half or some other constant multiple of \(v^2/r\)? Now that we have tools from calculus, we can address this issue straight on.
The figure shows a diagram of the situation. There is a satellite in circular orbit. (Earth hasn’t been included in the diagram.) Annotating one point of the orbit is a vector, \({\mathbf v}_1\), which represents the velocity of the satellite at that point in the orbit. The velocity vector is tangent to the orbit itself; it is instantaneous velocity. One-hundred eighty degrees opposite \({\mathbf v}_1\) is another velocity vector, \({\mathbf v}_3\) that has the same length as \({\mathbf v}_1\) but faces in exactly the opposite direction: \({\mathbf v}_3 = -{\mathbf v}_1\).
The change in the velocity vector over half the orbital time is simple: \({\mathbf v}_3 - {\mathbf v}_1 = {\mathbf v}_3 + {\mathbf v}_3 = 2 {\mathbf v}_3\).
Now calculus comes in: the change in velocity is the integral with respect to time of acceleration over the time to complete half an orbit. \[\int_{t=\text{start}}^{t=\text{end}} {\mathbf a}\, dt = 2 {\mathbf v}_3\]
We can simplify by setting the “start” time to zero. The end time is how long it takes to complete half an orbit. This will be the distance covered divided by the speed. The half circumference of the orbit is \(\pi r\). The speed of the satellite is \(|v|\). So the end time is \(\pi r/ v\).
Now we will take a false step. (You may not see it as such yet, but heads up!) The acceleration is constant: the satellite is always a constant distance from the center of the Earth. That is the nature of circular orbits. So the integral is simple:
\[\int_{t=\text{start}}^{t=\text{end}} {\mathbf a}\, dt = \int_{t=0}^{t=\pi r /v} a\, dt = a \int_{t=0}^{t=\pi r /v} dt = a \pi r/v = 2v .\] The rightmost equals relationship comes from our previous analysis of the change in velocity in half an orbit. Solving \(a \pi r/v = 2 v\) we get \[a = \frac{2}{\pi} \frac{v^2}{r} \neq \frac{v^2}{r}\] This half-an-orbit analysis gives a different answer for the relationship between acceleration and velocity than we used in the earlier calculation. At least one of them is wrong.
Where is the flaw in reasoning? First, although the magnitude of the acceleration is constant, the acceleration is a vector which is certainly not constant as the satellite moves through the orbit. And, being a vector, we need to keep track of the changing components of the vector. Referring to the diagram, only the “horizontal” component of the acceleration contributes to the change in velocity from point 1 to point 3, because that change is entirely horizontal.
Look at an intermediate point between 1 and 3. The vector \({\mathbf v}_2\) is shown at an angle \(\theta\) from the \({\mathbf v}_1\). At point 2, the acceleration vector is directed (as always) toward the center of the orbit. The horizontal component of the acceleration vector is \(a \sin(\theta)\), as you can see from the trigonometry of the situation. The previous integral should have been written in terms of the horizontal component of the acceleration:
\[\int_{t=0}^{t=\pi r/v} |{\mathbf a}|\,\sin(\theta)\, dt \] Keep in mind that \(\theta\) is a function of \(t\). The relationship is \[\theta = v t / r \ \ \implies\ \ \ d\theta = \frac{v}{r}dt\]
We’ve written the differential of the relationship because we will substitute for \(t\) and \(dt\) to translate the integral to be solely in terms of \(\theta\): \[\int_{\theta=0}^{\theta = \pi} |{\mathbf a}| \sin(\theta)\frac{r}{v}\, d \theta = |{\mathbf a}| \frac{r}{v} \int_{\theta=0}^{\theta = \pi} \sin(\theta)\, d \theta\] The integral involves one of the basic modeling functions, so we’ve memorized the answer.
- What is \[\int_{\theta=0}^{\theta = \pi} \sin(\theta)\, d \theta \ \text{?}\]
0
2
\(-\cos(\theta)\)
\(- \pi \cos(\theta)\)
question id: differential-orbit-2
- Set \[|{\mathbf a}| \frac{r}{v}\int_{\theta=0}^{\theta = \pi} \sin(\theta)\, d \theta = 2 v\] and solve for \(a\). Which one of these is it?
\(a = 2 \frac{v^2}{r}\)
\(a = \frac{v^2}{r}\)
\(a = 4 \frac{v^2}{r}\)
\(a = \frac{2}{\pi} \frac{v^2}{r}\)
question id: differential-orbit-3
No answers yet collected