Chap 37 Exercises

$$$$

Exercise 1 The output of a function, being a quantity, has dimension and units. Suppose the dimension of the output of a function $v(t)$ is $L/T$, for instance, meters-per-second.

The anti-derivative function $V(t)\equiv \int v(t)dt$ will also have dimension and units.

Recall that in constructing the anti-derivative using the Euler method, we multiply the values of $v(t)$ times some small increment in the input, $h$. Therefore the dimension of the output of $V(t)$ will be $[v(t)][t]$. So if $[v(t)]=L/T$, the dimension $[V(t)][t]=LT/T=L$. Units for such a dimension would be, for instance, meters. This makes sense, since if you accumulate velocity (meters-per-sec) over an interval of time (sec) you end up with the distance travelled (meters).

Suppose you know the acceleration $a(t)$ of an object as a function of time. The dimension of acceleration is $L/T^2$.

1. What is the dimension of $$\int a(t)dt\text{?}$$

$L/T^3$

$L$

$LT$

$L/T$

$L{T}^2$

question id: monkey-light-stove-1

Suppose you know the power consumed by an appliance $p(t)$ as a function of time. Typically appliances have a cycle and use different amounts of power during different parts of the cycle. (Think of a clothes washer.)

2. What will be the dimension of $\int p(t)dt\text{?}$

energy

force

acceleration

length

question id: monkey-light-stove-2

Exercise 2 This activity uses the “Graph-antiD” web app which enables you to visualize the anti-derivative function in terms of areas. To use the app, click-drag-and-release to mark part of the domain of the function being displayed.

Note in draft

Convert the app using ShinyLive and embed it here.

To answer these questions correctly, you must set the “Shape of function” box to 864.

A. From the graph, roughly estimate $${\int }_0^{3}f(t)dt$$ Choose the closest numerical value from the following. You could use either graph for this caclulation, but $F(t)$ will be simpler algebra.

-46

-26

0

3

19

26

question id: tiger-tug-shoe-1

B. to construct the anti-derivative whose value at time $t=-3$ will be zero, what constant of integration $C$ should you add to the $F(t)$ shown.

-120

-80

-50

0

50

80

120

question id: tiger-tug-shoe-2

C. Examining the stock at time $t=0$, you observe that there are 40 units. Roughly how much stock will there be at $t=5$?

-25

-15

0

15

25

question id: tiger-tug-shoe-3

D. You start with a stock of 100 units at time $t=-2$. At roughly what time $t$ will the stock be half of this?

-1.2

-0.3

0.5

1.2

1.8

The stock will never fall so low.

question id: tiger-tug-shoe-4

E. Your stock finally runs out at time $t=2.5$. When did you have 120 units in stock?

$t=-4$

$t=-3$

$t=0$

There was never such a time.

question id: tiger-tug-shoe-5

F. After decreasing for a long time, the stock finally starts to increase from about $t=2.5$ onward. What about $f(t=2.5)$ tells you that $F(t=2.5)$ is increasing?

The derivative is at a minimum.

The derivative is negative

The derivative is near zero.

The derivative becomes positive and stays positive.

The derivative is at a maximum.

question id: tiger-tug-shoe-6

G. Find the argmin $t^{\star }$ of $f(t)$ and note the sign of $f(t^{\star }).$ What does this tell you about $F(t^{\star })$.

$t^{\star }$ is also the argmin of $F()$.

$F(t^{\star })$ is decreasing at its steepest rate.

$F(t^{\star })$ is increasing at its slowest rate.

$F(t^{\star })$ is increasing at its steepest rate.

$t^{\star }$ is the argmax of $F()$

question id: tiger-tug-shoe-7

H. What is the average flow into stock over the period $-5\le t\le 1$. (If the flow is outward from stock, that is the same as a negative inward flow.)

-30

-20

0

10

question id: tiger-tug-shoe-8

I. Which of the following is an interval when the average flow is approximately zero?

$-1.3\le t\le 1.1$

$0.8\le t\le 5$

$-5\le t\le 0$

None of the above

question id: tiger-tug-shoe-9

J. From the graph, estimate $${\int }_2^{-4}f(t)dt$$ Choose the closest numerical value from the following.

-120

-60

60

120

None of these answers are close to being right.

question id: tiger-tug-shoe-10

Exercise 3 Consider this function, $f(t)$:

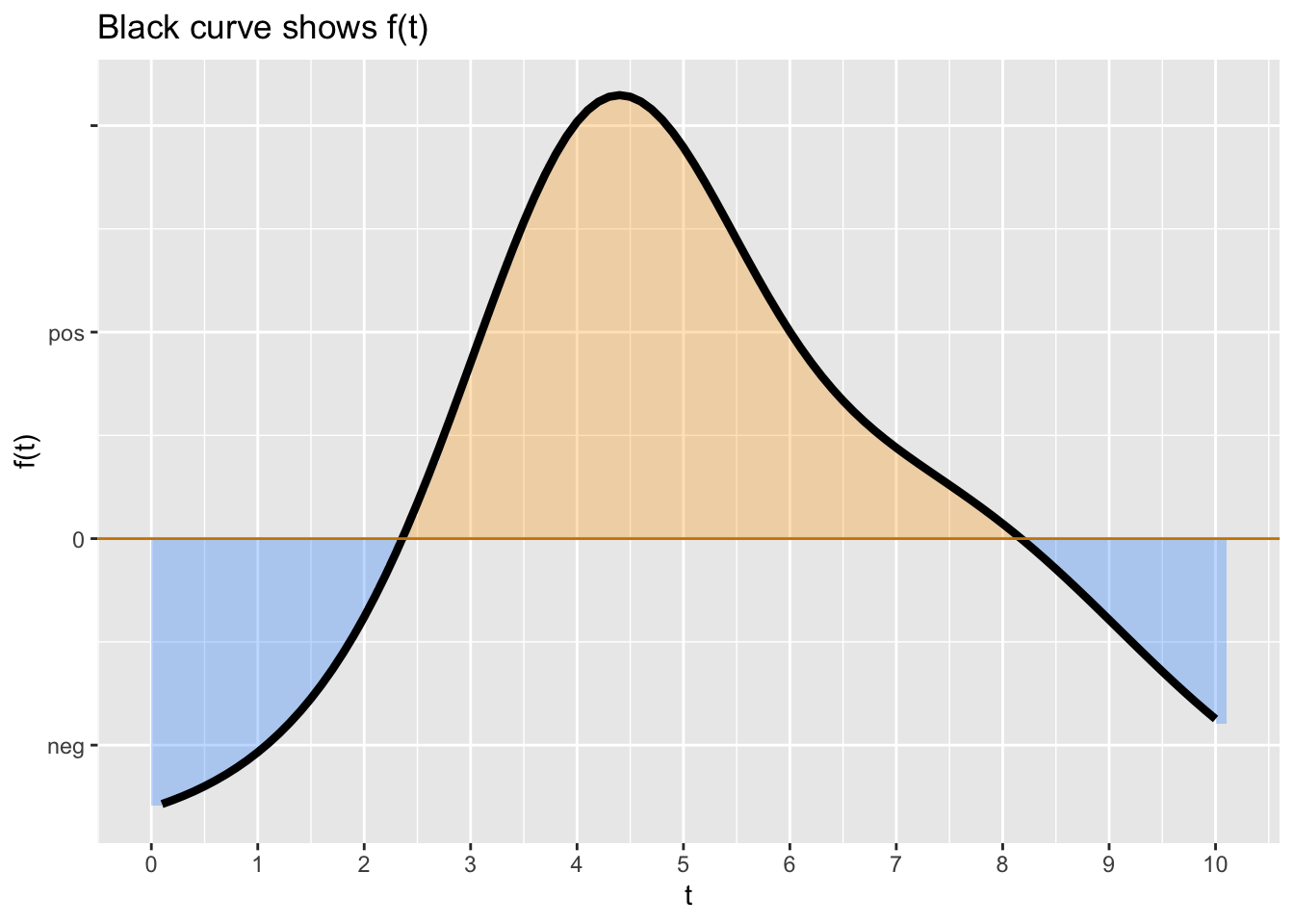
Assume that the “area” of each small box on the graph is the product of 1 Watt $\times$ 1 second.

1. What is $${\int }_1^{2}f(t)dt\text{?}$$ (Choose the closest answer. The units are in Watt-seconds.)

-3.2       -1.4       0       2.5       3.3       6.1      

question id: seahorse-choose-canoe-a1

$$\text{Let}A={\int }_1^{3}f(x)dx\text{and}B={\int }_2^{4}f(x)dx$$

A       B       They are the same size      

question id: seahorse-choose-canoe-2

$$\text{Let}A={\int }_3^{1}f(t)dt\text{and}B={\int }_4^{2}f(t)dt$$

3. Which is bigger, A or B?

A       B       They are the same size      

question id: seahorse-choose-canoe-3

Consider the function $$g(x)\equiv {\int }_4^{x}f(t)dt$$ for the next three questions

4. Which is bigger, $g(8)$ or $g(9)$?

$g(8)$       $g(9)$       They are the same size       Trick question! There can be no such function $g(x)$ since $f()$ is a function of $t$      

question id: seahorse-choose-canoe-4

5. Is $g(2.5)$ positive or negative?

positive       zero       negative      

question id: seahorse-choose-canoe-5

6. At what value of $x$ is $g(x)=0$?

2       3       4       5       6       7       8      

question id: seahorse-choose-canoe-6

$$\text{Let}h(x)\equiv {\int }_0^{x}f(t)dt$$

7. At what value of $x$ is $h(x)\approx 0$?

1       2       3       4       5       6      

question id: seahorse-choose-canoe-7

${\partial }_{x}h(x)$ is a function. When we write ${\partial }_{x}h(3)$ we mean to evaluate that function for an input value of $x=3$.

${\partial }_{x}h(3)$       ${\partial }_{x}h(4)$       Can’t tell.      

question id: seahorse-choose-canoe-8

$$\text{Let}y(x)\equiv {\int }_4^{x}f(t)dt$$

Here are four different graphs.

slice_plot(F(x) - F(4) ~ x, domain(x=0:10)) |>
  gf_labs(title = "(A)")

slice_plot(F(4) - F(x) ~ x, domain(x=0:10)) |>
  gf_labs(title = "(B)")

slice_plot(F(6) - F(x) ~ x, domain(x=0:10)) |>
  gf_labs(title = "(C)")

slice_plot(abs(F(4) - F(x)) ~ x, domain(x=0:10)) |>
  gf_labs(title = "(D)")

9. Which of the graphs shows $y(x)$?

A       B       C       D      

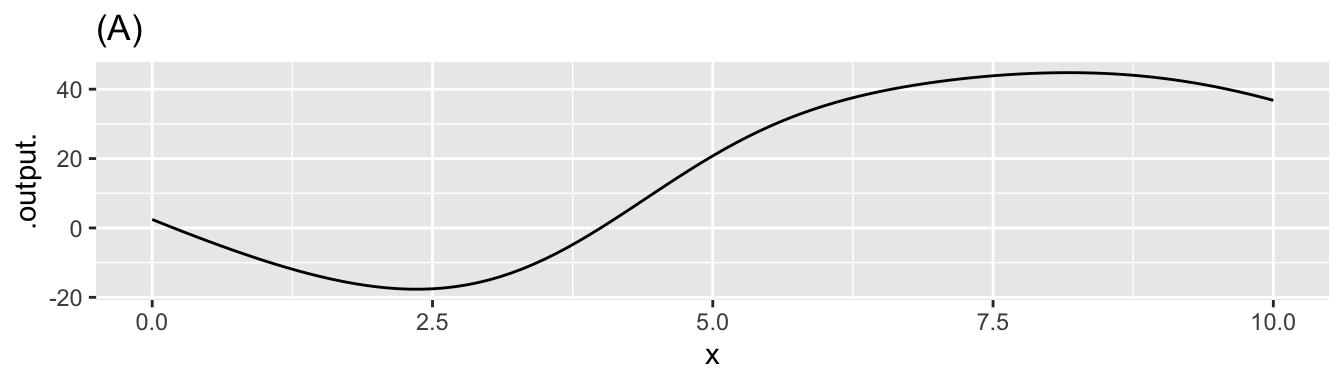
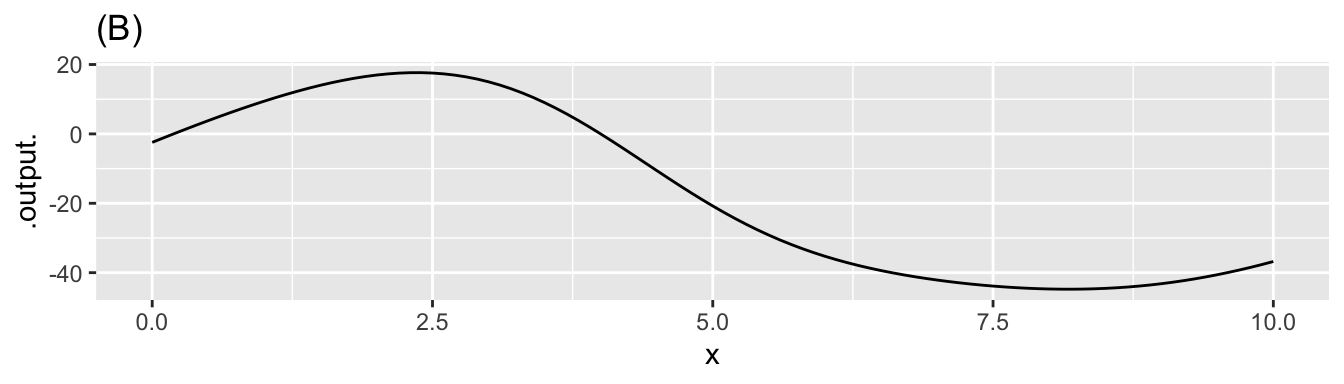
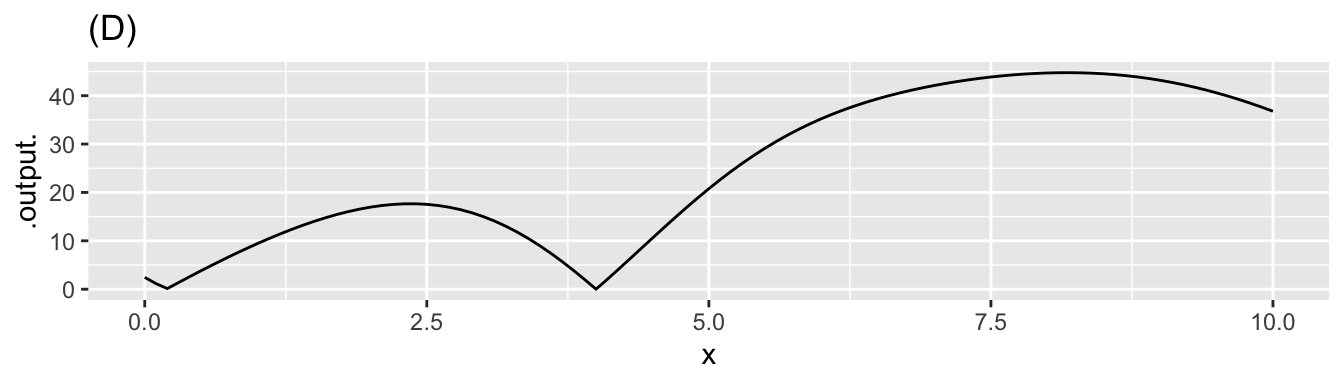
question id: seahorse-choose-canoe-9

Exercise 4 Consider this sequence: 4, 5, 3, 1, 2

1. What is the sum?

14

15

16

17

question id: cumsum5-1

2. What is the cumulative sum?

The sequence 4, 9, 12, 13, 15

The sequence 2, 3, 6, 11, 15

The sequence 0, 4, 9, 13, 15

question id: cumsum5-2

3. Which entry in the cumulative sum matches the sum?

The first

The last

None of them

All of them

question id: cumsum5-3

4. Will the answer to part (3) always be true for a cumulative sum?

Yes       No      

question id: cumsum5-4

Exercise 5 The result of applying the Euler method to a function is also another function, but it comes in the form of a vector of numbers all ready to be displayed graphically. So keep in mind the the function produced by Euler will be known only over a specified domain, just as the graph of a function covers only the specified domain. For instance, Active R chunk 1 shows the graph of the natural logarithm function over the domain $1\le x\le 21$.

Active R chunk 1

1

2

slice_plot(log(x) ~ x, domain(x = 1:21), npts=11) |>

  gf_point()

The command in the sandbox is a little different than the usual slice_plot(). We’ve added on two things:

1. An argument npts=11 which says to use 11 discrete values of the input in plotting the graph.

2. A second graphics layer that shows a dot at each input point where slice_plot() evaluated the function. Behind the seemingly smooth curves that slice_plot() produces is really a discrete set of points each of which is the output of the function at some numerical input.

In our typical use of slice_plot() we leave out the dots and show only the straight line segments that connect the positions where the dots would be plotted. If the positions are spaced closely enough, your eye will not see the joints between successive straight lines and you will perceive the graph as a smooth curve.

1. For the graph of the log function over the domain $1\le x\le 21$ with npts=11 (that is, the initial command shown in the sandbox), what is the horizontal spacing between the discrete $x$ values?

1       2       4       5      

question id: slicedots1

Now take away the npts= argument. This will implicitly set npts to a default value, which is what we have been using for most plots in this course.

2. What is the default value of npts in slice_plot()?

25       50       100       200       500       1000      

question id: slicedots2

We could use a much larger value for npts, but there is no reason so long as a smaller value produces a graph faithful to the function being graphed.

Keeping the domain the same, $1\le x\le 21$, plot out a sinusoid with a period of 0.3 using the default npts: $g(x)\equiv \sin (2\pi x/0.3)$. The graph, which shows about 67 cycles of the sinusoid, will not look much like a sinusoid. In particular, although the sine function should reach from -1 to 1 over each cycle, the graph does not.

125       150       200       400       800       1600       3200      

question id: slicedots3

Exercise 9 Methods such as Euler are tedious, ideal for the computer. So let’s look at some basic R functions for implementing the Euler Method when we know the function to be anti-differentiated $f(x)$, the step size $h$, and the domain $a\le x\le b$. At the heart of the implementation is a function cumsum(), the “cumulative sum.” This does something very simple. The cumulative sum of the sequence 1, 2, 3, 4 is another sequence: 1, 3, 6, 10.

Active R chunk 2 has commands for using cumsum() to approximate the anti-derivative of a function $f()$ over the domain $a\le x\le b$.

Active R chunk 2:

question id: falcon-hurt-pot-essay

1

2

3

4

5

6

7

8

9

10

11

12

13

f <- makeFun(sin(2*pi*x/0.3) ~ x) # the function to be anti-differentiated.

a <- 1 # the lower bound.

b <- 2 # the upper bound.

h <- 0.01 # the step size

# all of the discrete x values based on a, b, and h

x_discrete <- seq(a, b, by = h)

# all of the values of f(x) when the 

# discrete x values are used as the input

f_discrete <- f(x_discrete) 

 # the discrete values of the anti-derivative, F(x)

F_discrete <- cumsum(h * f_discrete)

gf_point(F_discrete ~ x_discrete) %>%

  slice_plot(f(x) ~ x, color = "gray", bounds(x=c(a,b)))

Here is a function:

g <- makeFun(exp(-0.2*(x^2))~x)

Use Active R chunk 2 to find and plot the anti-derivative of $g(x)$ over the domain $-6\le x\le 6$.

Your task: Describe the shape of $G(x)$. Your description can be one word from earlier in the book, if you choose it carefully. If your graph looks like a straight line, you did not appropriately change the domain above.

Exercise 6 The graphic, from The Economist news magazine, shows the number of elective treatments (e.g. minor surgery, etc.) by the British National Health Service over the period January 2019 to April 2021. The point of the graph is to show the extent to which people avoided medical treatment due to the Covid-19 pandemic, which started to become severe in March 2020. (The January/February treatment numbers for 2020 line up pretty exactly with the 2019 numbers.)

According to the graphic, how many fewer treatements were there in the 12 months of 2020 compared to the 12 months of 2019? (Choose the best of the following answers.)

About 500,000

About 2,000,000

About 6,000,000

About 10,000,000

question id: ape-bit-sheet-1

Activities

Exercise 7 Using the Euler method find $\int f(t)dt$ over the interval $t_0=0$ to $t_{end}=1$. The $t$ quantity is in steps of $h=0.01$.

$t$	${\partial }_{t}f(t)$	$\int f(t)dt$
0	0.399	0.5
0.01	0.242
0.02	0.054
0.03	0.399

Exercise 8 Anti-derivatives are useful when you know how a quantity is changing but don’t (yet) know the quantity itself.

Imagine, for instance, that you are sailing on a straight course across a large lake. Your friend, in the bow of the boat, uses a radar gun to record velocity at each instant. Velocity is, of course, the change in position over time. The recording lasts for 12 minutes, that is 0.20 hour, as shown in the Sailing-over-time app.

Note in draft

Embed the sailing over time app here using ShinyLive.

How far did the boat travel during the 0.2-hour recording? Distance equals velocity times time. If the velocity were constant, say 4 mph, the distance would be 4 mph $\times$ 0.2 hour $=0.8$ miles. But the velocity is changing over the recording. To do the velocity-times-time calculation we use the standard calculus method of dividing up time into a series of very short time intervals, each of duration $dt$. Over each of these short time intervals, the boat travels a short distance. For instance, for the interval covering time $t=0.05$ hour, the boat travels distance $\text{vel}(0.05)dt$.

Suppose we set $dt=0.05$ hour. There would be 5 such 0.05-hour-long intervals over the entire 0.2-hour recording, shown as colored segments in the graph. In the first interval, the boat has velocity that we will approximate as $\text{vel}(0)$ and travels roughly $\text{vel}(0)dt$. During the second 0.05-hour-long interval, the boat’s velocity is $\text{vel}(0.05)$ and travels $\text{vel}(0.05)dt$. During the third interval, the velocity is $\text{vel}(0.15)$ and travels $\text{vel}(0.15)dt$. The total distance travelled is $$\text{vel}(0.00)dt+\text{vel}(0.05)dt+\text{vel}(0.10)dt+\dots +\text{vel}(0.15)dt=$$ $$[\text{vel}(0.00)+\text{vel}(0.05)+\text{vel}(0.10)+\dots +\text{vel}(0.15)]dt=$$

$$14.01\text{miles/hour}\times 0.05\text{hour}$$

Each of the terms like $\text{vel}(0.10)dt$ is a velocity times a duration of time. This multiplies a quantity on the horizontal axis by a quantity on the vertical axis. Graphically, such a multiplication can be shown as an “area.” But keep in mind that the units of this “area” are miles. (Vertical axis: miles-per-hour. Horizontal axis: hours. Multiply the two quantities: hours $\times$ miles/hour = miles.)

If you have changed the length of dt and/or clicked show the multiplication as an area, You can scroll up and see the changes to the graph.

The sum above amounts to adding up all those rectangular “areas,” each of which is in the units “miles.”

1. What is the dimension of the quantity $14.01\text{miles/hour}\times 0.05\text{hour}$?

LT^2

L

L/T

T

T/L

question id: sailing-over-time-1

Making dt small

Another way to write the formula given in the previous section uses the mathematical “sum” symbol: $$\text{vel}(0.00)dt+\text{vel}(0.05)dt+\text{vel}(0.10)dt+\dots +\text{vel}(0.15)dt=\sum _{i=0}^4\text{vel}(t_i)dt$$ The $t_i$ in $\sum \text{vel}(t_i)$ is a notation for the horizontal location of the $i^{th}$ segment. Since the length of each segment is 0.05 hour in this example, $t_i$ is $i\times 0.05$.

Using the sum notation, we can easily write down the calculation if we set $dt$ to be 0.01 hour rather than 0.05 hour in which case will have 20 segments covering the 0.2 hours of the recording: $$\sum _{\text{i}=0}^{19}\text{vel}(t_i)dt$$ Or, with $dt$ set to one-thousandth of an hour there will be 200 segments: $$\sum _{\text{i}=0}^{199}\text{vel}(t_i)dt$$ Evaluate the commands in Active R chunk 3 to calculate the first two of the sum formulas with $dt=0.01$ hour and $dt=0.001$ hour respectivly. (The function $\text{vel}(t)$ is given as vel().)

Active R chunk 3

1

2

3

4

5

6

7

8

9

10

11

12

13

# Ignore the next two lines. They define the velocity function.

tmp <- doodle_fun(~ t, seed=638)

vel <- makeFun(1+(10+tmp(30*(t-0.08)))/4 ~ t)

# You should start here

# dt = 0.01 hours

segs <- 0:19 # 20 segments to cover 0.2 hours

time_points <- 0.01 * segs

sum(vel(time_points) * 0.01)

# dt = 0.001 hour

segs2 <- 0:199 # 200 segments to cover in minutes

time_points2 <- 0.001 * segs2 # every 0.001 hour

sum(vel(time_points2) * 0.001)

Then revise the commands in Active R chunk 3 to calculate the sum over 2000 segments, corresponding to a segment length of 0.0001 hour.

2. When $dt=$ 0.0001 hour, there are 2000 segments over the 0.2 hour recording. What is $$\sum _{i=0}^{1999}\text{vel}(t_i=0.0001\times i)dt\text{?}$$

0.7716       0.7772       0.7888       0.7903      

question id: sailing-over-time-2

Repeat the calculation, but for 20,000 segments, each of duration 0.00001 hours.

3. When $dt=$ 0.00001, there are 20,000 segments over the 0.2 hr recording. What is $$\sum _{i=0}^{19999}\text{vel}(t_i=0.00001\times i)dt\text{?}$$

0.7816       0.7843       0.7886       0.7889      

question id: sailing-over-time-3

You can see that for $dt⪅0.01$, the answer does not depend much on $dt$. In fact, the radar gun will round off the velocity to the nearest 1/10 mph, so any real accuracy by taking $dt$ very small is illusory.

You can also see that the calculations themselves are a bit finicky. You have to get the number of segments to correspond to the choice of $dt$ and convert the segment id number to time properly. Then you add in something of size $dt/2$ to be in the middle of the segment.

To save all this trouble in accumulating the velocity or any other change function, we simply say, “Integrate the function $\text{vel}(t)$ over the interval $0\le t\le 0.2$.” In symbols, we write this $${\int }_0^{0.2}\text{vel}(t)dt$$ meaning “sum from time $t=0$ until time $t=0.2$.”

The anti-derivative of $\text{vel}(t)$, which we can write $\text{VEL}(t)$, tells the sum of the $\text{vel}(t)dt$ segments. Plug in a numerical value for that argument and out will come a numerical value for $\text{VEL}()$ at that input. The one argument of $\text{VEL}(t)$ is the end time of the accumulation.

There is no explicit mention of the start time. To indicate that $\text{VEL}(t)$ does not tell the start time of accumulation, we write the anti-derivative generally as $\text{VEL}(t)+C$. The $C$ is unknown because the start time is unknown.

Once we know a start time, we can figure out $C$. Suppose the start time is $0$. And let’s make, for the sake of argument, the end time be $t=0$ as well. Common sense tells us that when the start time and the end time are the same, nothing gets accumulated. Thus, whatever $C$ might be, $\text{VEL}(0)+C=0$, giving us $C=-\text{VEL}(0)$.

Now suppose we want to know how much is accumulated over the interval $3\le t\le 8$. The start time is 3, so the relevant choice of $C$ is $C=-\text{VEL}(3)$.

Now, evaluate the anti-derivative at the end time, 8. The amount accumulated to time 8 is $\text{VEL}(8)+C$. But we now know $C$ and can re-write the amount accumulated in the interval $3\le t\le 8$ as $\text{VEL}(8)-\text{VEL}(3)$.

In general, if $F(x)$ is the anti-derivative of $f(x)$ then the accumulation of $f(x)$ over the interval $a\le x\le b$ will be $${\int }_a^{b}f(x)dx=F(b)-F(a)$$

Note that, because we specified the start at $x=a$, we do not have to include the constant $C$. In a way, $C$ is just a reminder that $F(x)$ tells us the accumulation up to $x$, but without our knowing where the accumulation started.

The anti-derivative lets us split accumulation problems into two pieces:

1. Find the anti-derivative $F(x)$ of $f(x)$, the quantity being accumulated.
2. When we want to know the amount accumulated over any specified interval $a\le x\le b$, simply plug in $a$ and $b$, like this: $F(b)-F(a)$.

We can use any technique we like to find the anti-derivative $F(x)$. When $f(x)$ is one of our basic modeling functions with a linear interior function (e.g. $f(x)=e^{kx}$), we can always write down the formula for the anti-derivative using the rules we have studied (e.g. $F(x)=\frac{1}{k}{e}^{kx}$). Or, if we have a formula for $f(x)$ that is more difficult, we can look for a solution that someone else has figured out. But, often, there will be no simple formula for $F(x)$. In that case, we can use numerical methods like the sum-of-segments we used to find the distance sailed.

The antiD() R operator takes as input a tilde expression defining the function $f()$, e.g. exp(k*x) ~ x. As an output, it produces a function $F(x)$. Let’s try:

Use the sandbox and the antiD() function to accumulate the boat’s velocity over the interval from $t=0.0$ to $0.2$.

Active R chunk 4

1

2

VEL <- antiD(vel(t) ~ t)

# Calculate the definite integral

AntiD as notation for Euler

At minute 4:26 (that is, hour 0.0710), the boat sailed by a red marker buoy. Then at minute 6:45 (that is, hour 0.1075), the boat passed a blue marker bouy. How far apart are the red and blue bouys?

This is an accumulation problem that we can denote as $${\int }_{0.0710}^{0.1075}\text{vel}(t)dt.$$ Use the anti-derivative $\text{VEL}(t)$ computed in the earlier sandbox to calculate the accumulated velocity times $dt$.

4. Which is the correct answer over the interval?

0.154 hours

0.154 meters

0.7889 hours

0.154 miles

0.7889 miles

question id: sailing-over-time-4

37-exercises.rmarkdown

No answers yet collected