Chap 26 Review

$$$$

Loading webR...

Exercise 1 In the polynomial $a_0+a_{x}x+a_{y}y+a_{xy}xy$, what is the term $a_{xy}xy$ called?

Interaction term       Quadratic term       Linear term       Constant term      

question id: Poly01

Exercise 2 In the polynomial $a_0+a_{x}x+a_{y}y+a_{xx}xx$, what is the coefficient on the interaction term?

0       $a_{xy}$       $a_{xx}$       $a_0$      

question id: Poly02

Exercise 3 Imagine a second-order polynomial in three inputs: $x$, $y$, and $z$, like this: $$b_0+b_{x}x+b_{y}y+b_{z}z+b_{xy}xy+b_{xz}xz+b_{xx}{x}^2+b_{yy}{y}^2+b_{z}z{z}^2.$$ All of the possible second-order (or less) terms are shown, except for one. Which term is missing?

the interaction between $y$ and $z$

the quadratic term in $z$

the linear term in $y$

the constant term

question id: Poly03

Exercise 4 Here is a function $f(x)$: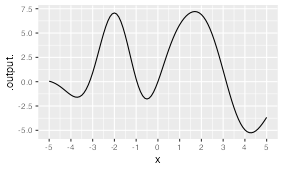

In the Taylor polynomial approximation to $f(x)$ centered at $x=-2,$ what will be the sign of the coefficient on the first-order term. Choose the best answer.

positive       zero       negative       no such coefficient exists in a Taylor polynomial      

question id: Poly04

Exercise 5 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=1$, what will be the sign of the coefficient on the first-order term. Choose the best answer.

positive       zero       negative       no such coefficient exists in a Taylor polynomial      

question id: Poly05

Exercise 6 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=1$, what will be the sign of the coefficient on the second-order term. Choose the best answer.

positive       zero       negative       no such coefficient exists in a Taylor polynomial      

question id: Poly06

Exercise 7 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=-4$, what will be the sign of the coefficient on the first-order term. Choose the best answer.

positive       zero       negative       no such coefficient exists in a Taylor polynomial      

question id: Poly07

Exercise 8 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=4$, what will be the sign of the coefficient on the second-order term. Choose the best answer.

positive       zero       negative       no such coefficient exists in a Taylor polynomial      

question id: Poly08

Exercise 9 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=4$, what will be the sign of the coefficient on the constant (zeroth-order) term. Choose the best answer.

positive       zero       negative       no such coefficient exists in a Taylor polynomial      

question id: Poly09

Exercise 10 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=3$, what will be the sign of the coefficient on the second-order term. Choose the best answer.

positive       zero       negative       no such term exists in a Taylor polynomial      

question id: Poly10

Exercise 11 Here is a function $f(x)$:

In the Taylor polynomial approximation to $f(x)$ centered at $x=0$, what will be the sign of the coefficient on the reciprocal term. Choose the best answer.

positive       zero       negative       no such term exists in a Taylor polynomial      

question id: Poly11

Exercise 12 Here is a function $g(x)$: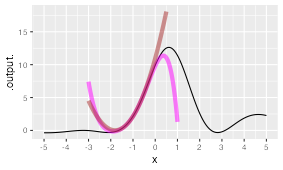

Two Taylor polynomials, centered on the same $x$ are shown. One is fifth-order, the other is third-order. Which is which?

The third-order polynomial is brown.       The third-order polynomial is magenta.      

question id: Poly12

Exercise 13 Here is a function $g(x)$: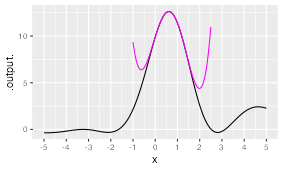

with a Taylor polynomial shown in magenta. What is the order of the polynomial?

zero       one       two       three       four      

question id: Poly13

26-review.rmarkdown

No answers yet collected