Chap 24 Review

$$$$

Loading webR...

Exercise 1 What is ${\partial }_{x}x$?

$0$       $1$       $x$       $y$      

question id: drill-partialderivatives-1

Exercise 2 What is ${\partial }_{x}y$?

$0$       $1$       $x$       $y$      

question id: drill-partialderivatives-2

Exercise 3 What is ${\partial }_{x}ax$?

$0$       $a$       $x$       $y$      

question id: drill-partialderivatives-3

Exercise 4 What is ${\partial }_{x}xy$?

$0$       $1$       $x$       $y$      

question id: drill-partialderivatives-4

Exercise 5 What is ${\partial }_{y}xy$?

$0$       $1$       $x$       $y$      

question id: drill-partialderivatives-5

Exercise 6 What is ${\partial }_{x}A{e}^{kt}$?

$0$       $Ak{e}^{kx}$       $t$      

question id: drill-partialderivatives-6

Exercise 7 What is ${\partial }_{t}A{e}^{kt}$?

$0$       $kA{e}^{kt}$       $kA{e}^{kx}$       $tA{e}^{kt}$      

question id: drill-partialderivatives-7

Exercise 8 What is ${\partial }_{x}Ax{e}^{kt}$?

$0$       $Ax{e}^{kt}$       $Akx{e}^{kt}$       $A{e}^{kt}$      

question id: drill-partialderivatives-8

Exercise 9 What is ${\partial }_{t}Ax{e}^{kt}$?

$0$       $Ak{e}^{kt}$       $Akx{e}^{kt}$       $A{e}^{kt}$      

question id: drill-partialderivatives-9

Exercise 10 What is ${\partial }_x[a_0+a_{1}x+a_2{x}^2]$?

$a_1+a_{2}x$       $a_1+2a_{2}x$       $a_0+a_{1}x$       0      

question id: drill-partialderivatives-10

Exercise 11 What is ${\partial }_y[a_0+a_{1}x+a_2{x}^2]$?

$a_1+a_{2}x$       $a_1+2a_{2}x$       $a_1+2a_{2}y$       0      

question id: drill-partialderivatives-11

Exercise 12 What is ${\partial }_x[a_0+a_{1}y+a_2{y}^2]$?

$a_1+a_{2}x$       $a_1+2a_{2}x$       $a_1+2a_{2}y$       0      

question id: drill-partialderivatives-12

Exercise 13 What is ${\partial }_x[a_0+a_{1}x+b_{1}y+cxy]$?

$a_1+cy$       $a_1$       $a_1+b1+c$       $a_1+c$      

question id: drill-partialderivatives-13

Exercise 14 What is ${\partial }_y[a_0+a_{1}x+b_{1}y+cxy]$?

$b_1+cx$       $b_1$       $a_1+b1+c$       $b_1+c$      

question id: drill-partialderivatives-14

Exercise 15 What is ${\partial }_x{\partial }_y[a_0+a_{1}x+b_{1}y+cxy]$? (Usually we would write ${\partial }_{xy}$ instead of ${\partial }_x{\partial }_y$, but they amount to the same thing.)

$c$       $a_1$       $b_1$       $0$      

question id: drill-partialderivatives-15

Exercise 16 What is ${\partial }_x{\partial }_x[a_0+a_{1}x+b_{1}y+cxy]$? (Usually we would write ${\partial }_{xx}$ instead of ${\partial }_x{\partial }_x$, but they amount to the same thing.)

$c$       $a_1$       $b_1$       $0$      

question id: drill-partialderivatives-16

Exercise 17 What is ${\partial }_x{\partial }_x[a_0+a_{1}x+b_{1}y+cxy+a_2{x}^2+b_2{y}^2]$? (Usually we would write ${\partial }_{xx}$ instead of ${\partial }_x{\partial }_x$, but they amount to the same thing.)

$2a_2$       $a_2$       $c+a_2$       $0$      

question id: drill-partialderivatives-17

Exercise 18 What is ${\partial }_y{\partial }_x[a_0+a_{1}x+b_{1}y+cxy+a_2{x}^2+b_2{y}^2]$? (Usually we would write ${\partial }_{yx}$ instead of ${\partial }_y{\partial }_x$, but they amount to the same thing.)

$c$       $2a_2$       $2b_2$       $0$      

question id: drill-partialderivatives-18

Exercise 19 What is ${\partial }_x\left[A{x}^n{y}^m\right]$?

$An{x}^{n-1}{y}^m$       $Anm{x}^{n-1}{y}^{m-1}$       $Am{x}^n{y}^{m-1}$       $A{y}^m$      

question id: drill-partialderivatives-19

Exercise 20 What is ${\partial }_y\left[A{x}^n{y}^m\right]$?

$An{x}^{n-1}{y}^m$       $Anm{x}^{n-1}{y}^{m-1}$       $Am{x}^n{y}^{m-1}$       $Am{y}^{m-1}$      

question id: drill-partialderivatives-20

Exercise 21 What is ${\partial }_{xy}\left[A{x}^n{y}^m\right]$?

$An{x}^{n-1}{y}^{m-1}$       $Anm{x}^{n-1}{y}^{m-1}$       $Am{x}^n{y}^{m-1}$       $Am{x}^{n-1}{y}^{m-1}$      

question id: drill-partialderivatives-21

Exercise 22 What is ${\partial }_x[f(x)+y]$?

${\partial }_{x}f(x)$       ${\partial }_{x}f(x)+1$       ${\partial }_{x}f(x)+y$       $0$      

question id: drill-partialderivatives-22

Exercise 23 What is ${\partial }_x[f(x)+g(y)]$?

${\partial }_{x}f(x)$       ${\partial }_{x}f(x)+{\partial }_{x}g(y)$       ${\partial }_{x}f(x)+{\partial }_{y}g(y)$       $0$      

question id: drill-partialderivatives-23

Exercise 24 What is ${\partial }_y[f(x)+g(y)]$?

${\partial }_{x}f(x)$       ${\partial }_{x}g(y)$       ${\partial }_{y}g(y)$       0      

question id: drill-partialderivatives-24

Exercise 25 What is ${\partial }_x{\partial }_y[f(x)+g(y)]$?

${\partial }_{x}f(x)$       ${\partial }_x{\partial }_{y}g(y)$       ${\partial }_{y}g(y)$       0      

question id: drill-partialderivatives-25

Exercise 26 What is ${\partial }_y{\partial }_y[f(x)+g(y)]$?

${\partial }_{y}g(y)$       1       ${\partial }_{yy}g(y)$       0      

question id: drill-partialderivatives-26

Exercise 27 What is ${\partial }_{y}f(x)g(y)$?

${\partial }_{y}g(y)$

$f(x){\partial }_{y}g(y)$

0

$g(y){\partial }_{y}f(x)+f(x){\partial }_{y}g(y)$

question id: drill-partialderivatives-27

Exercise 28 What is ${\partial }_{y}h(x,y)g(y)$?

${\partial }_{y}g(y)$       $g(y){\partial }_{y}h(x,y)$       0       $ g(y) _y h(x,y) + h(x,y) _y g(y)$      

question id: drill-partialderivatives-28

Exercise 29 What is ${\partial }_{x}h(x,y)g(y)$?

${\partial }_{x}h(x,y)$       $g(y){\partial }_{x}h(x,y)+h(x,y){\partial }_{x}g(y)$       $g(y){\partial }_{x}h(x,y)$       $g(y){\partial }_{y}h(x,y)$      

question id: drill-partialderivatives-29

Exercise 30 What is ${\partial }_{yx}h(x,y)g(y)$?

${\partial }_{yx}h(x,y)$

$g(y){\partial }_{yx}h(x,y)+h(x,y){\partial }_{y}g(y)$

$({\partial }_{y}g(y))({\partial }_{x}h(x,y))+g(y)({\partial }_{yx}h(x,y))$

$({\partial }_{x}g(y))({\partial }_{x}h(x,y))+g(y)({\partial }_{xx}h(x,y))$

question id: drill-partialderivatives-30

Exercise 31 What is the “with-respect-to” input in ${\partial }_{y}xy$?

$x$       $y$       $1$      

question id: drill-partialderivatives-31

Exercise 32 What is the “with-respect-to” input in ${\partial }_{x}y$?

$x$       $y$       $1$      

question id: drill-partialderivatives-32

Exercise 33 What is the “with-respect-to” input in ${\partial }_{t}y$?

$t$       $y$       $1$      

question id: drill-partialderivatives-33

Exercise 34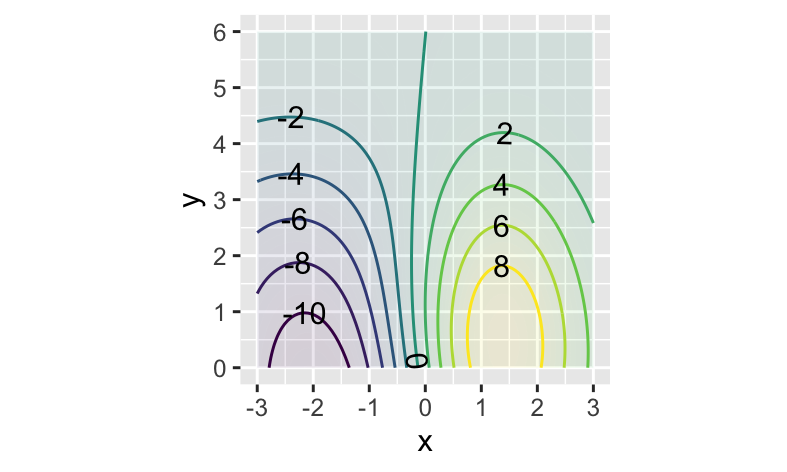
At which of these inputs is the function steepest in the x-direction?

$(x=0,y=6)$       $(x=1,y=5)$       $(x=-2,y=6)$       $(x=0,y=1)$      

question id: drill-Quiz-2-16

Exercise 35
At which of these inputs is the function practically flat?

$(x=0,y=6)$       $(x=1,y=2)$       $(x=-2,y=3)$       $(x=0,y=1)$      

question id: drill-Quiz-2-18

Exercise 36
You are standing on the input point $(x=-1,y=4)$. In terms of the compass points (where north would be up and east to the right), which direction points most steeply uphill from where you are standing.

NE       SE       SW       NW      

question id: drill-Quiz-2-19

Exercise 37
You are standing on the input point $(x=2,y=1)$. In terms of the compass points (where north would be up and east to the right), which direction points most steeply uphill from where you are standing.

NE       SE       SW       NW      

question id: drill-Quiz-2-20

24-review.rmarkdown

No answers yet collected