Chap 14 Review

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Figure 1: .

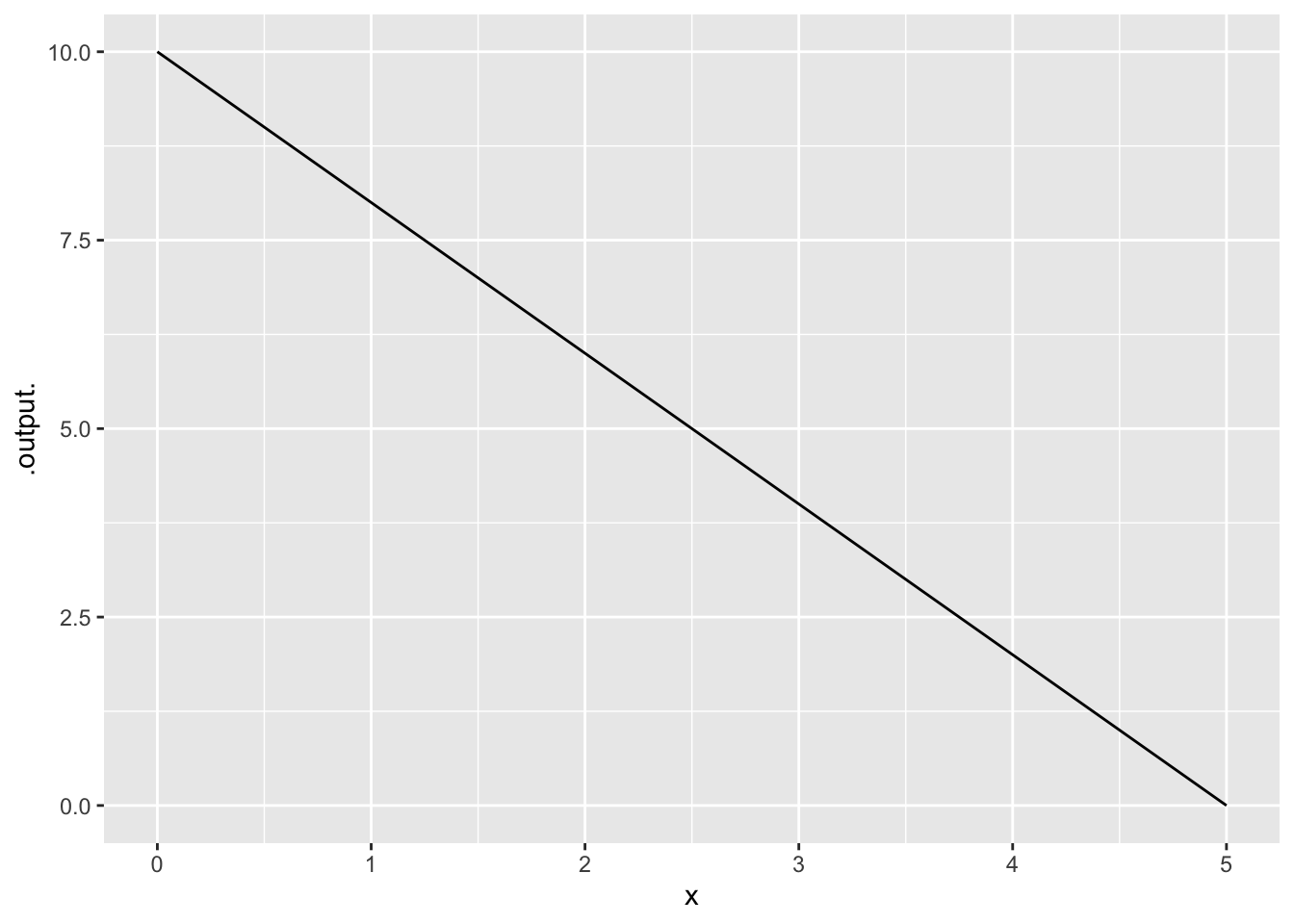
Exercise 1 What is the correct form for the relationship shown in Figure fig-exponential-neg

\(g(x) \equiv e^{10} e^{-2 x}\)

\(g(x) \equiv 10 e^{-2 x}\)

\(g(x) \equiv e^{10} e^{-1.5 x}\)

\(g(x) \equiv e^{-1.5} e^{10 x}\)

\(g(x) \equiv 10 x^{-1.5}\)

question id: drill-Scales-1

Exercise 2 Which of these is the better modeling relationship for the following scenario: Your data looks linear on a semi-log plot.

Power-law       Exponential       Logarithmic      

question id: drill-Scales-1b

Exercise 3 Which of these is the better modeling relationship for the following scenario: Your data looks linear on a log-log plot.

Power-law       Exponential       Logarithmic      

question id: drill-Scales-1c

Figure 2: .

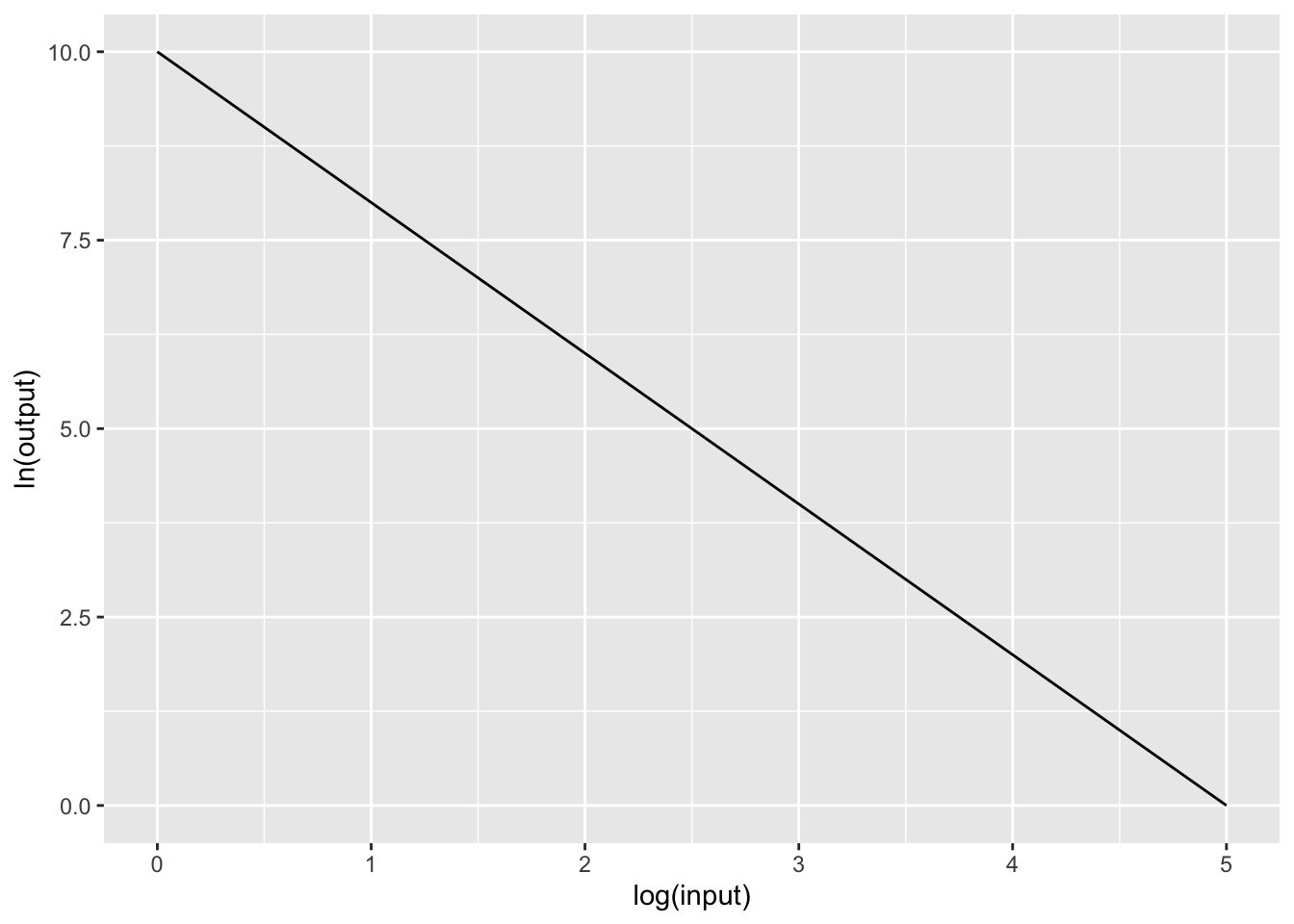
Exercise 4 What is the correct form for the relationship shown in Figure fig-power-law-neg?

\(g(x) \equiv 10 x^{-2}\)

\(g(x) \equiv e^{10} e^{-1.5 x}\)

\(g(x) \equiv e^{10} x^{-2}\)

\(g(x) \equiv e^10 x^{-1.5}\)

question id: drill-Scales-2

Figure 3: .

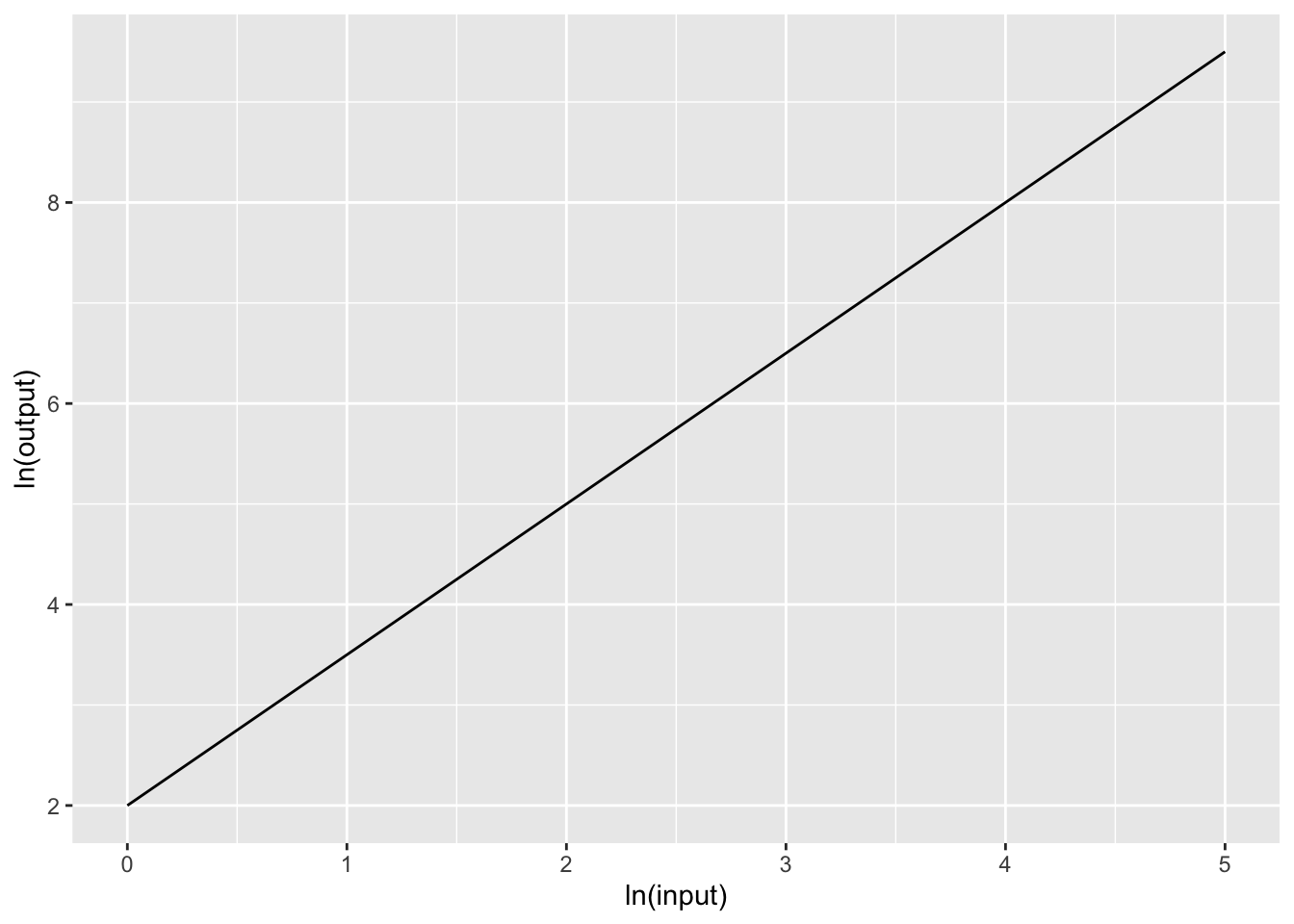
Exercise 5 What is the correct form for the relationship shown in Figure fig-power-law?

\(g(x) \equiv e^{2} e^{1.5 x}\)

\(g(x) \equiv 2 x^{1.5}\)

\(g(x) \equiv e^{2} x^{1.5}\)

\(g(x) \equiv e^{2} x^{2}\)

\(g(x) \equiv e^2 x^{-1.5}\)

question id: drill-Scales-3

Figure 4: .

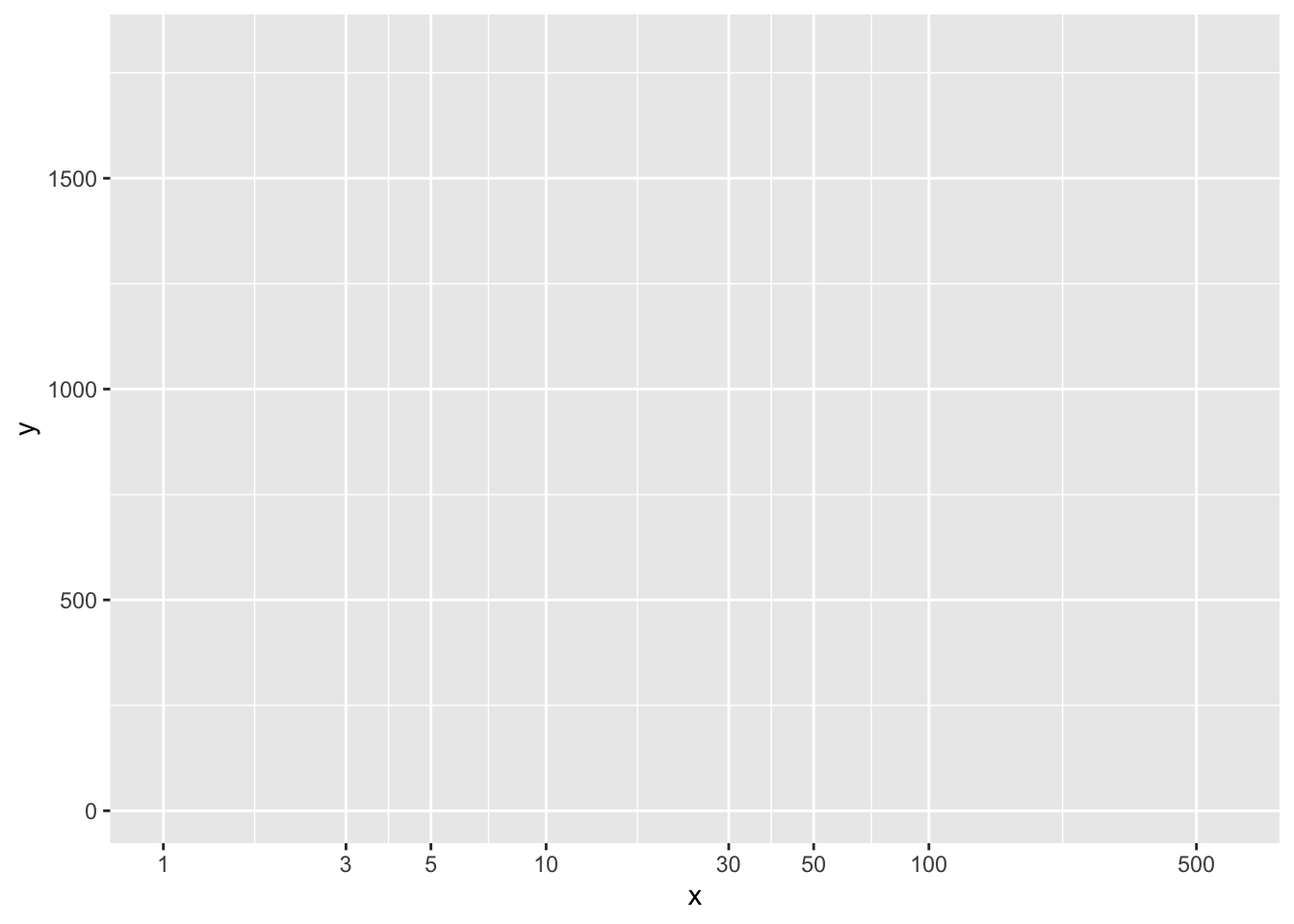
Exercise 6 Figure fig-scales-base2 shows a horizontal axis for a graph. How can you tell that this is a logarithmic axis?

The labels are all multiples of 2.

The labels are evenly spaced and each label is a factor of 2 larger than the previous one.

Trick question. It is not a log scale.

question id: drill-Scales-4

Figure 5: .

Exercise 7 Figure fig-scales-semidecade shows a horizontal axis for a graph. How can you tell that this is a logarithmic axis?

The labels are 1, 3, 5, 10, …

The labels are evenly spaced and each label is a factor of 3 larger than the previous one.

The 3 label is about halfway between the 1 and 10 label for each decade, and the 1 and 10 labels have the same spacing for every decade.

Trick question. It is not a log scale.

question id: drill-Scales-5

Figure 6: .

Exercise 8 Figure fig-scales-bogus shows a horizontal axis for a graph. How can you tell that this is a logarithmic axis?

The labels are 10, 20, 30, 40, …

Each label is 10 + the previous label.

The 3 label is about halfway between the 1 and 10 label for each decade, and the 1 and 10 labels have the same spacing for every decade.

Trick question. It is not a linear scale.

question id: drill-Scales-6

No answers yet collected