Chap 25 Review

$$$$

Loading webR...

Exercise 1 What is ${\partial }_{x}x$?

$0$       $1$       $x$       $y$      

question id: PD01

Exercise 2 What is ${\partial }_{x}y$?

$0$       $1$       $x$       $y$      

question id: PD02

Exercise 3 What is ${\partial }_{x}ax$?

$0$       $a$       $x$       $y$      

question id: PD03

Exercise 4 What is ${\partial }_{x}xy$?

$0$       $1$       $x$       $y$      

question id: PD04

Exercise 5 What is ${\partial }_{y}xy$?

$0$       $1$       $x$       $y$      

question id: PD05

Exercise 6 What is ${\partial }_{x}A{e}^{kt}$?

$0$       $Ak{e}^{kx}$       $t$      

question id: PD06

Exercise 7 What is ${\partial }_{t}A{e}^{kt}$?

$0$       $kA{e}^{kt}$       $kA{e}^{kx}$       $tA{e}^{kt}$      

question id: PD07

Exercise 8 What is ${\partial }_{x}Ax{e}^{kt}$?

$0$       $Ax{e}^{kt}$       $Akx{e}^{kt}$       $A{e}^{kt}$      

question id: PD08

Exercise 9 What is ${\partial }_{t}Ax{e}^{kt}$?

$0$       $Ak{e}^{kt}$       $Akx{e}^{kt}$       $A{e}^{kt}$      

question id: PD09

Exercise 10 What is ${\partial }_x[a_0+a_{1}x+a_2{x}^2]$?

$a_1+a_{2}x$       $a_1+2a_{2}x$       $a_0+a_{1}x$       0      

question id: PD10

Exercise 11 What is ${\partial }_y[a_0+a_{1}x+a_2{x}^2]$?

$a_1+a_{2}x$       $a_1+2a_{2}x$       $a_1+2a_{2}y$       0      

question id: PD11

Exercise 12 What is ${\partial }_x[a_0+a_{1}y+a_2{y}^2]$?

$a_1+a_{2}x$       $a_1+2a_{2}x$       $a_1+2a_{2}y$       0      

question id: PD12

Exercise 13 What is ${\partial }_x[a_0+a_{1}x+b_{1}y+cxy]$?

$a_1+cy$       $a_1$       $a_1+b1+c$       $a_1+c$      

question id: PD13

Exercise 14 What is ${\partial }_y[a_0+a_{1}x+b_{1}y+cxy]$?

$b_1+cx$       $b_1$       $a_1+b1+c$       $b_1+c$      

question id: PD14

Exercise 15 What is ${\partial }_x{\partial }_y[a_0+a_{1}x+b_{1}y+cxy]$? (Usually we would write ${\partial }_{xy}$ instead of ${\partial }_x{\partial }_y$, but they amount to the same thing.)

$c$       $a_1$       $b_1$       $0$      

question id: PD15

Exercise 16 What is ${\partial }_x{\partial }_x[a_0+a_{1}x+b_{1}y+cxy]$? (Usually we would write ${\partial }_{xx}$ instead of ${\partial }_x{\partial }_x$, but they amount to the same thing.)

$c$       $a_1$       $b_1$       $0$      

question id: PD16

Exercise 17 What is ${\partial }_x{\partial }_x[a_0+a_{1}x+b_{1}y+cxy+a_2{x}^2+b_2{y}^2]$? (Usually we would write ${\partial }_{xx}$ instead of ${\partial }_x{\partial }_x$, but they amount to the same thing.)

$2a_2$       $a_2$       $c+a_2$
      $0$      

question id: PD17

Exercise 18 What is ${\partial }_y{\partial }_x[a_0+a_{1}x+b_{1}y+cxy+a_2{x}^2+b_2{y}^2]$? (Usually we would write ${\partial }_{yx}$ instead of ${\partial }_y{\partial }_x$, but they amount to the same thing.)

$c$       $2a_2$       $2b_2$       $0$      

question id: PD18

Exercise 19 What is ${\partial }_x\left[A{x}^n{y}^m\right]$?

$An{x}^{n-1}{y}^m$       $Anm{x}^{n-1}{y}^{m-1}$       $Am{x}^n{y}^{m-1}$       $A{y}^m$      

question id: PD19

Exercise 20 What is ${\partial }_y\left[A{x}^n{y}^m\right]$?

$An{x}^{n-1}{y}^m$       $Anm{x}^{n-1}{y}^{m-1}$       $Am{x}^n{y}^{m-1}$       $Am{y}^{m-1}$      

question id: PD20

Exercise 21 What is ${\partial }_{xy}\left[A{x}^n{y}^m\right]$?

$An{x}^{n-1}{y}^{m-1}$       $Anm{x}^{n-1}{y}^{m-1}$
      $Am{x}^n{y}^{m-1}$       $Am{x}^{n-1}{y}^{m-1}$      

question id: PD21

Exercise 22 What is ${\partial }_x[f(x)+y]$?

${\partial }_{x}f(x)$       ${\partial }_{x}f(x)+1$       ${\partial }_{x}f(x)+y$       $0$      

question id: PD22

Exercise 23 What is ${\partial }_x[f(x)+g(y)]$?

${\partial }_{x}f(x)$       ${\partial }_{x}f(x)+{\partial }_{x}g(y)$       ${\partial }_{x}f(x)+{\partial }_{y}g(y)$       $0$      

question id: PD23

Exercise 24 What is ${\partial }_y[f(x)+g(y)]$?

${\partial }_{x}f(x)$       ${\partial }_{x}g(y)$       ${\partial }_{y}g(y)$       0      

question id: PD24

Exercise 25 What is ${\partial }_x{\partial }_y[f(x)+g(y)]$?

${\partial }_{x}f(x)$       ${\partial }_x{\partial }_{y}g(y)$       ${\partial }_{y}g(y)$       0      

question id: PD25

Exercise 26 What is ${\partial }_y{\partial }_y[f(x)+g(y)]$?

${\partial }_{y}g(y)$       1       ${\partial }_{yy}g(y)$       0      

question id: PD26

Exercise 27 What is ${\partial }_{y}f(x)g(y)$?

${\partial }_{y}g(y)$       $f(x){\partial }_{y}g(y)$       0       $g(y){\partial }_{y}f(x)+f(x){\partial }_{y}g(y)$      

question id: PD27

Exercise 28 What is ${\partial }_{y}h(x,y)g(y)$?

${\partial }_{y}g(y)$       $g(y){\partial }_{y}h(x,y)$       0       $ g(y) _y h(x,y) + h(x,y) _y g(y)$      

question id: PD28

Exercise 29 What is ${\partial }_{x}h(x,y)g(y)$?

${\partial }_{x}h(x,y)$       $g(y){\partial }_{x}h(x,y)+h(x,y){\partial }_{x}g(y)$       $g(y){\partial }_{x}h(x,y)$       $g(y){\partial }_{y}h(x,y)$      

question id: PD29

Exercise 30 What is ${\partial }_{yx}h(x,y)g(y)$?

${\partial }_{yx}h(x,y)$

$g(y){\partial }_{yx}h(x,y)+h(x,y){\partial }_{y}g(y)$

$({\partial }_{y}g(y))({\partial }_{x}h(x,y))+g(y)({\partial }_{yx}h(x,y))$

$({\partial }_{x}g(y))({\partial }_{x}h(x,y))+g(y)({\partial }_{xx}h(x,y))$

question id: PD30

Exercise 31 What is the “with-respect-to” input in ${\partial }_{y}xy$?

$x$       $y$       $1$      

question id: PD31

Exercise 32 What is the “with-respect-to” input in ${\partial }_{x}y$?

$x$       $y$       $1$      

question id: PD32

Exercise 33 What is the “with-respect-to” input in ${\partial }_{t}y$?

$t$       $y$       $1$      

question id: PD33

Exercise 34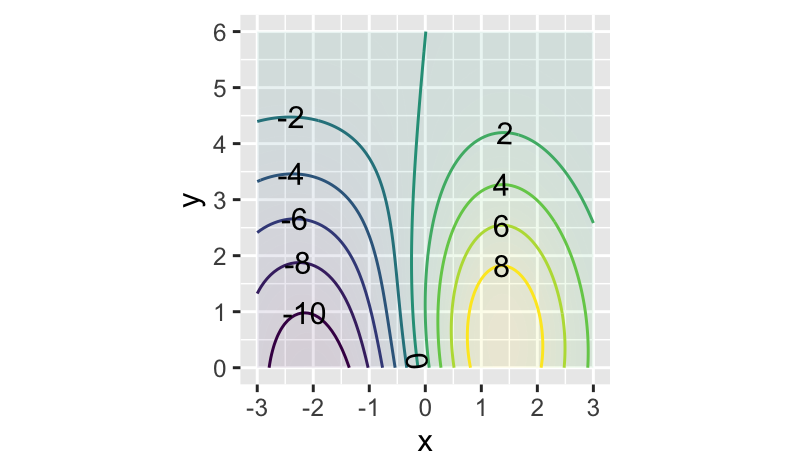
You have been hiking all day and have reached map coordinate (x=2, y=2). You are completely exhausted. Time for a break. You want to walk along the hill, without any change of elevation. Which compass direction should you head in to get started?

W or SE

SE but not NW

NW but not SE

NE or SW

question id: r2-21

25-review.rmarkdown

No answers yet collected