Chap 28 Review

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1  

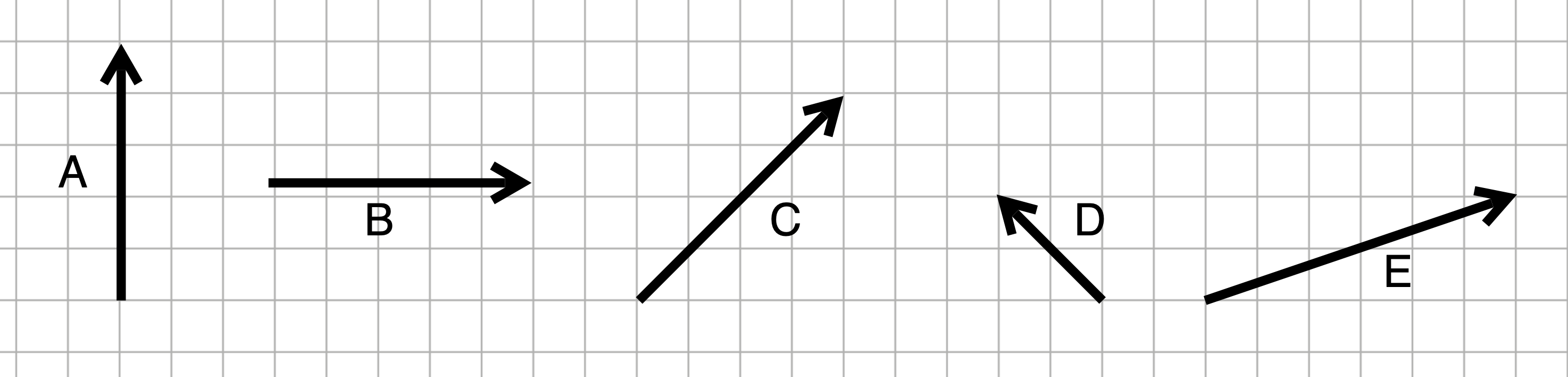
  1. What is \(\vec{C}^T\cdot\vec{D}\)?
-8       0       6       10       14       16       24       30       34       40       42      

question id: bear-fight-closet-A

  1. What is \(\vec{E}^T\cdot\vec{B}\)?
-8       0       6       10       14       16       24       30       34       40       42      

question id: bear-fight-closet-B

  1. What is \(\vec{A}^T\cdot\vec{E}\)?
-8       0       6       10       14       16       24       30       34       40       42      

question id: bear-fight-closet-C

  1. What is \(\vec{D}^T\cdot\vec{E}\)?
-8       0       6       10       14       16       24       30       34       40       42      

question id: bear-fight-closet-D

  1. What is \(\left(\vec{A}+\vec{B}\right)^T\cdot\vec{C}\)?
-8       0       6       10       14       16       24       30       34       40       42      

question id: bear-fight-closet-E

  1. What is \(\left(\vec{C}+\vec{D}\right)^T\cdot\vec{E}\)?
-8       0       6       10       14       16       24       30       34       40       42      

question id: bear-fight-closet-F

Exercise 2 Here are twelve labeled vectors, A through M. There is a thirteenth vector, labeled “Null vector,” that is a vector of length zero, so it cannot be drawn as an arrow. Note that the direction of the null vector does not matter since the vector length is zero.

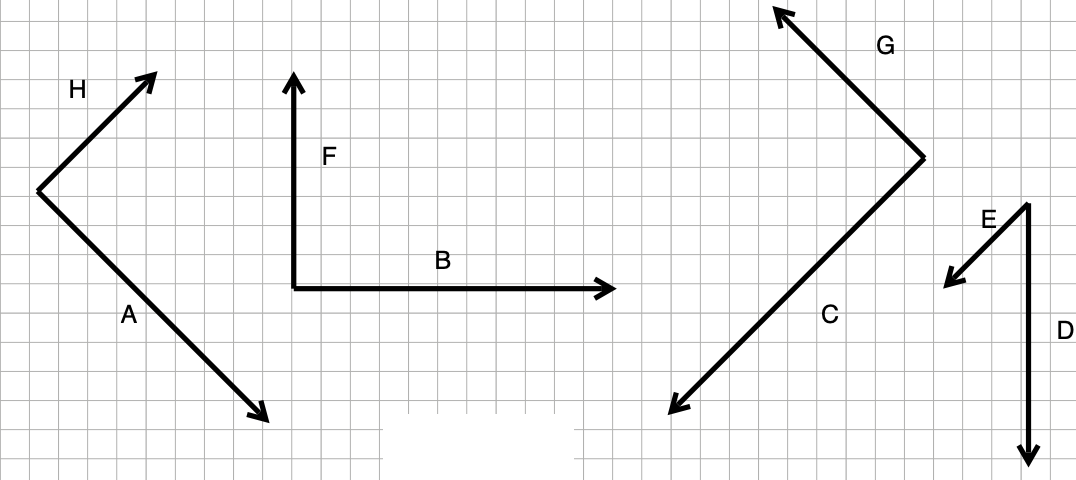
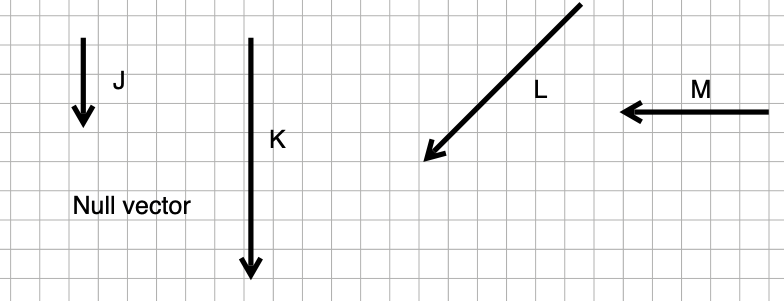
Each of the following statements is of the form, “\(\vec{v}\) projected onto \(\vec{u}\) gives \(\vec{w}\). Say whether the statement is true or false.

  1. \(\vec{A}\) projected onto \(\vec{D}\) gives \(\vec{K}\)

True

False

question id: beech-build-shirt-1

  1. \(\vec{D}\) projected onto \(\vec{E}\) gives \(\vec{L}\)

True

False

question id: beech-build-shirt-2

  1. \(\vec{J}\) projected onto \(\vec{E}\) gives the null vector.

True

False

question id: beech-build-shirt-3

  1. \(\vec{H}\) projected onto \(\vec{A}\) gives the null vector
True       False      

question id: beech-build-shirt-4

  1. \(\vec{J}\) projected onto \(\vec{K}\) gives \(\vec{D}\)
True       False      

question id: beech-build-shirt-5

  1. \(\vec{C}\) projected onto \(\vec{D}\) gives \(\vec{L}\)
True       False      

question id: beech-build-shirt-6

  1. \(\vec{L}\) projected onto \(\vec{B}\) gives the null vector
True       False      

question id: beech-build-shirt-7

  1. \(\vec{E}\) projected onto \(\vec{C}\) gives \(\vec{E}\)
True       False      

question id: beech-build-shirt-8

  1. \(\vec{G}\) projected onto \(\vec{C}\) gives the null vector.
True       False      

question id: beech-build-shirt-9

  1. \(\vec{E}\) projected onto \(\vec{D}\) gives \(\vec{J}\)
True       False      

question id: beech-build-shirt-10

  1. \(\vec{A}\) projected onto \(\vec{B}\) gives \(\vec{K}\)
True       False      

question id: beech-build-shirt-11

  1. \(\vec{H}\) projected onto \(\vec{A}\) gives the null vector
True       False      

question id: beech-build-shirt-12

  1. \(\vec{F}\) projected onto \(\vec{C}\) gives \(\vec{H}\)
True       False      

question id: beech-build-shirt-13

  1. \(\vec{C}\) projected onto \(\vec{E}\) gives \(\vec{E}\)
True       False      

question id: beech-build-shirt-14

  1. \(\vec{E}\) projected onto \(\vec{G}\) gives the null vector
True       False      

question id: beech-build-shirt-15

  1. \(\vec{G}\) projected onto \(\vec{B}\) gives \(\vec{C}\)
True       False      

question id: beech-build-shirt-16

Exercise 3 Consider the two vectors \[\vec{u} \equiv \left(\begin{array}{c}3\\4\end{array}\right) \ \ \ \mbox{and} \ \ \ \vec{w} \equiv \left(\begin{array}{c}1\\1\\1\\1\end{array}\right) \]

Hint: You don’t need the computer to do the calculations for this problem.

What is the length of the vector \(\vec{u}\)?

2       5       25       None of the above      

question id: octopus-sell-mattress-1

What is the length of the vector \(\vec{w}\)?

2       4       6       None of the above      

question id: octopus-sell-mattress-2

What is \(w^T \circ u\)?

7

14

It does not exist.

question id: octopus-sell-mattress-3

Exercise 4 Here are several vectors:

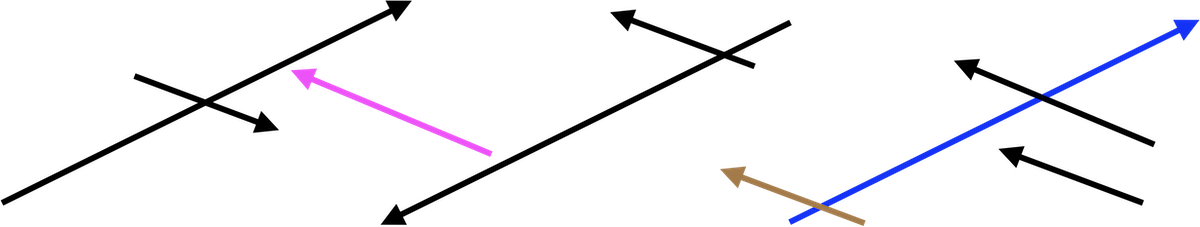
  1. Remembering that mathematical vectors have only two properties—length and direction—how many mathematically different vectors are being shown.
Answer

Five. Color is not a property of a mathematical vector. Orientation, however, is.

  1. Measure the length of each vector. (Hint: Use a ruler! You can round to the nearest millimeter.)

  2. Find the included angle between the \(\color{blue}{\text{blue}}\) and \(\color{brown}{\text{brown}}\) vectors. (Your answer should be correct to within \(\pm 15^\circ\).)

Answer

About 135 degrees. Note that the orientation makes a difference. The angle is measured with the vectors placed tail to tail.

  1. Find the included angle between the \(\color{magenta}{\text{magenta}}\) and \(\color{blue}{\text{blue}}\) vectors.
Answer

Magenta points in the same direction as brown, so the answer is the same as in the previous question.

  1. Find the included angle between 0.7 times the \(\color{blue}{\text{blue}}\) vector and -11.3 times the \(\color{brown}{\text{brown}}\).
Answer

The scaling does not matter except that the negative sign for the brown vector means that its orientation will be reversed. This means that the included angle will be 45 degrees, not 135 degrees as in the previous two questions.

Exercise 5 Suppose \[\vec{\mathbf u} \equiv \left(\begin{array}{c}4\\-3\end{array}\right) \ \ \mbox{and}\ \ \vec{\mathbf v} \equiv \left(\begin{array}{c}2\\2\end{array}\right)\ .\] The following questions ask you to compute the length of the vector given. (If none of the available choices are exactly right, choose the closest.)

\(3 \vec{u}\)

3

4

5

6

10

15

16

question id: rhinosaurus-break-knob-1

  1. \(-2 \vec{u}\)

3

4

5

6

10

15

16

question id: rhinosaurus-break-knob-2

\(-\vec{v}\)

3

4

5

6

10

15

16

question id: rhinosaurus-break-knob-3

\(\vec{u}+ \vec{v}\)

3

4

5

6

10

15

16

question id: rhinosaurus-break-knob-4

\(2 \vec{u} - 5 \vec{v}\)

3

4

5

6

10

15

16

question id: rhinosaurus-break-knob-5

No answers yet collected