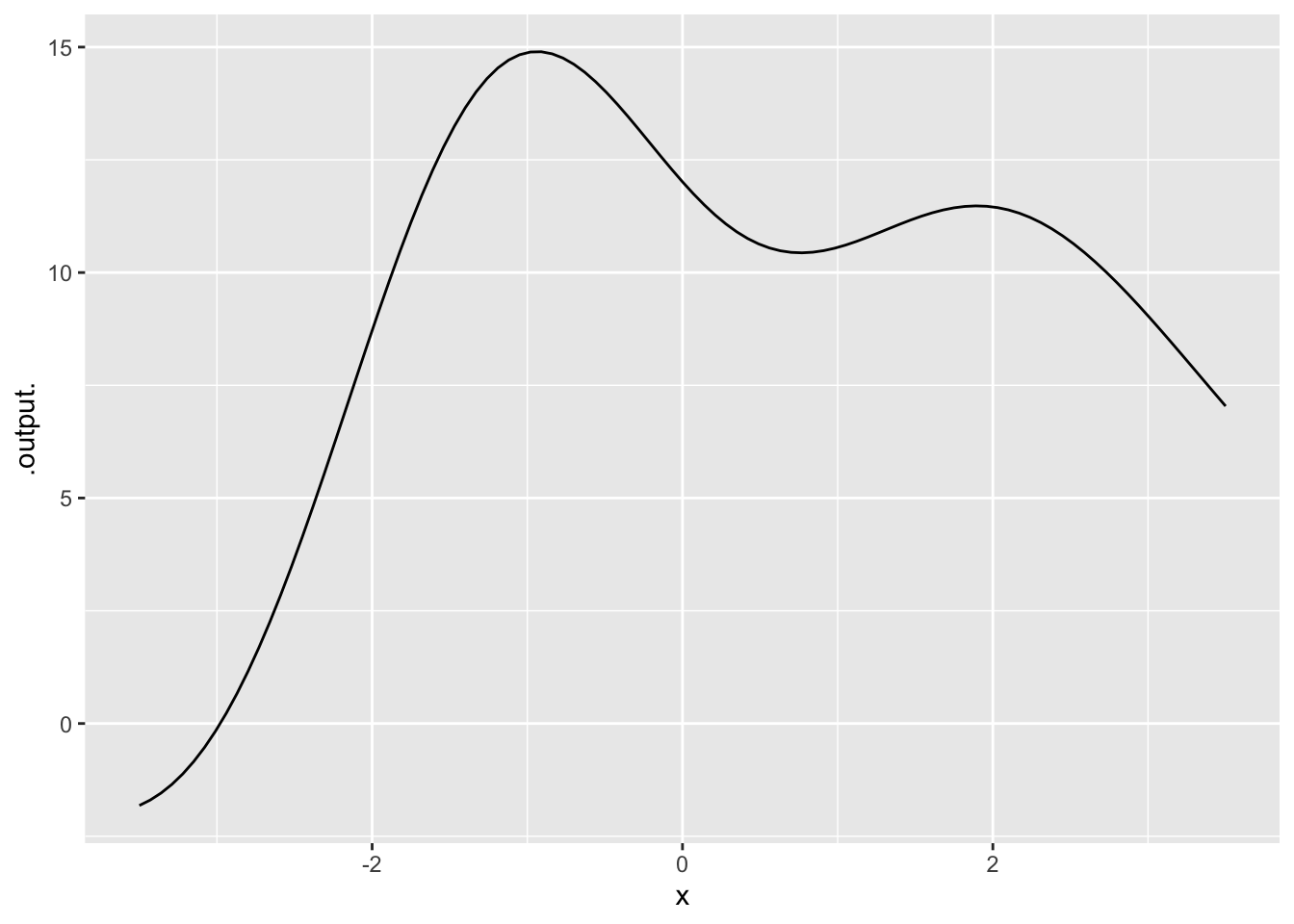
Chap 4 Exercises
\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]
Exercise 1
- To judge from Figure 1, say what the function output is from each of the following input values. (Select the closest from among the available choices.)
- Output when input is \(x = -3\)
question id: eagle-toss-cotton-1a
- Output when input is \(x = -2\)
question id: eagle-toss-cotton-1b
- Output when input is \(x = -1\)
question id: eagle-toss-cotton-1c
- Output when input is \(x = 0\)
question id: eagle-toss-cotton-1d
- Output when input is \(x = 1\)
question id: eagle-toss-cotton-1e
- Output when input is \(x = 2\)
question id: eagle-toss-cotton-1f
- Output when input is \(x = 3\)
question id: eagle-toss-cotton-1g
- For each of the following, find the \(x\) that produces the given output. (Select the closest from among the available choices.) (Click here to re-display Figure 1.)
- \(f(x)\) gives 5
question id: eagle-toss-cotton-2a
- \(f(x)\) gives 20
question id: eagle-toss-cotton-2b
- \(f(x)\) gives 10
question id: eagle-toss-cotton-2c
- \(f(x)\) gives 0
question id: eagle-toss-cotton-2d
- \(f(x)\) gives 12.5
question id: eagle-toss-cotton-2e
Exercise 2 Which of the following R expressions creates a graph of the function \(\sin(z)\) with a graphics domain from \(-4\leq z \leq 5\)?
slice_plot(sin(x), domain(x=-4:5))
slice_plot(sin(z) ~ x, domain(x=-4:5))
slice_plot(sin(z), domain(z=-4:5))
slice_plot(sin(z) ~ z, domain(z=-4:5))
question id: gspf-01
Hint: You can try copying and running each expression in Active R chunk 1 to check your answer.
Exercise 3
Consider the code used to Active R chunk 2:
- What is the
|>doing at the end of line 2 in the graphics-making command?
It is punctuation to help the human reader distinguish between the two lines.
It connects the graphics produced by the first slice_plot() application to the second slice_plot(), so that the new (orange) curve will be added on top of the old.
It signals the computer to display the graphic.
It identifies the command as one of the functions we use in CalcZ, something like ‘branding.’
question id: gg-code1
- Why is the
|>at the end of the second line rather than at the beginning of the third?
No good reason. You could do it either way.
Without the |>, the computer wouldn’t know to look to the next line of code to include in the overall chain of commands.
That’s a mistake. |> should always be at the start of a command.
question id: gg-code2
- What is the
|>operator called?
question id: gg-code3
- What is an expression like
2*x*(1-x/100) ~ xcalled?
A tilde expression
A wiggle expression
An argument
Applying a function to an argument
question id: gg-code4
- Which of the two function graphs is drawn in dark orange?
The quadratic growth function
The piecewise growth function
Not enough information is given in the code to be sure.
question id: gg-code5
- How come
"orange3"is in quotes?
Without quotes, the R interpreter would look for an R object named orange3
Because the color isn’t pure orange.
The computer will use red if it is available in the graphics subsystem. If not, it will use dashes.
question id: gg-code6
- What would happen if the
|>were removed from the code? (Hint: Try it!)
An error message would be thrown.
Only the black curve would be drawn.
The black and red curve would be drawn in separate graphics frames.
question id: gg-code7
- There is a pipe symbol at the end of the second line, but not at the end of the first. Why not?
The computer figures out where the pipes should go.
At the end of the first line, we are still among the arguments for the slice_plot() command. Pipes go only after the closing parenthesis of a command.
There should have been a pipe at the end of the first line. The author made a mistake.
question id: gg-code8
- Why is there a
domain()argument given in the first line but not the second?
Because of the pipe, the domain is inherited by the second part of the pipeline.
The author was careless.
The piecewise function does not require a domain, because its derivative is not continuous.
question id: gg-code9
Exercise 4 Consider the two commands in the following interactive chunk:
The first line defines a function named f().
The second line attempts to plot f() over the graphics domain -10 to 10. But it doesn’t work.
- What’s wrong?
f() is not a proper name for a function.
The first argument should be a tilde expression like f ~ x.
The first argument should be a tilde expression like f(x) ~ x.
question id: first-argument-a
- Fix the code in the chunk so that the command works. (Make sure to run the fixed code so that your answer will be submitted along with the rest.)
Exercise 5 Each of the following commands is intended to graph a given function over a graphic domain running from zero to ten. But none of them work, as is. Fix each command so that it works. (Suggestion: Try running the command, as is. Then look at the error message to get a hint how to fix things. Also, make sure to run the code after you have fixed the command in order for your answers to be submitted along with the rest.)
Exercise 6 The R/mosaic command in Active R chunk 3 will draw a graph of the function specified by the tilde expression.
- Why is the graph a flat line?
Because the vertical scale has been chosen inappropriately.
Because the output of the function is always 15, regardless of the value of the input \(y\).
Because the graphics domain is not long enough.
question id: constant-fun-a
- The vertical scale of the graph is very limited, covering a range of only \(15 \pm 0.05\). This scale was selected automatically by
slice_plot()because the function itself does not give any context for what the vertical scale should be. You can set the vertical scale manually by piping the graphics command into this expression,gf_lims(y = c(0, 20)). Make this change to the R-chunk and verify that the scale is indeed what is indicated.
Exercise 7 The function f() produced by doodle_fun() has two inputs. A contour plot is an appropriate way to visualize the function. In this exercise, you’re going to play with the location of contours. The contours_at argument tells what levels of the output should be marked with a contour.
Place a new contour inbetween the two contours at output levels 0 and 5.
By trial and error, find the output level whose contour goes through the origin of the (x,y) input space.
question id: draw-contours-value
Exercise 8 Look through all the contour plots in this document (except Figure 2) to see if it ever happens that two contours at different output levels intersect.
Chemists are familiar with “phase diagrams” that show the different configurations for a mass of molecules as a function of temperature and pressure. Figure 2 is for carbon-dioxide, CO\(_2\). You read off the form of the substance in exactly the same way you read a contour plot.
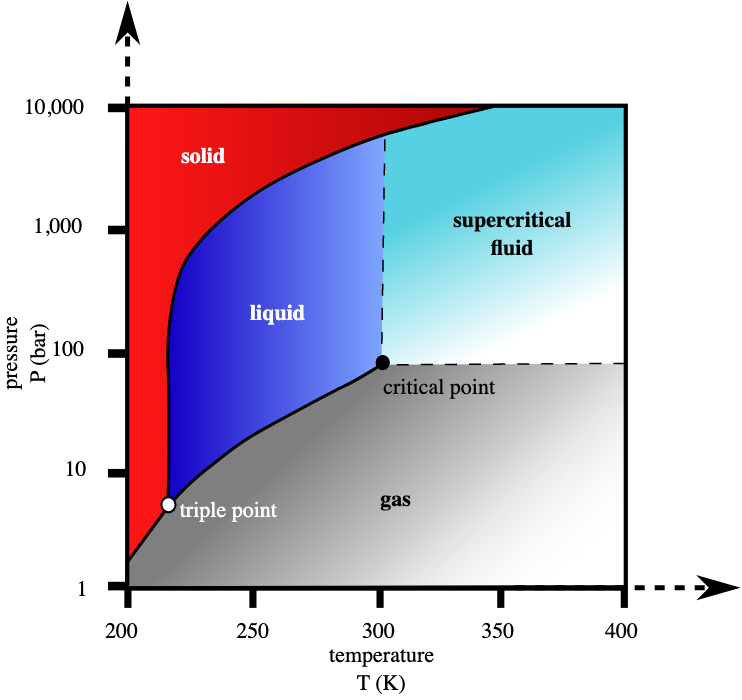
In chemistry, the “contours” are called “phase transitions.” But unlike genuine contour plots, the different phase transitions can intersect. In chemistry, such an intersection point is called a “critical point.”
Practice with contour plots
Exercise 9 The contour plot below is marked with several colored lines which represent slices through the surface. Your job is to match these up with the slice plots presented below.
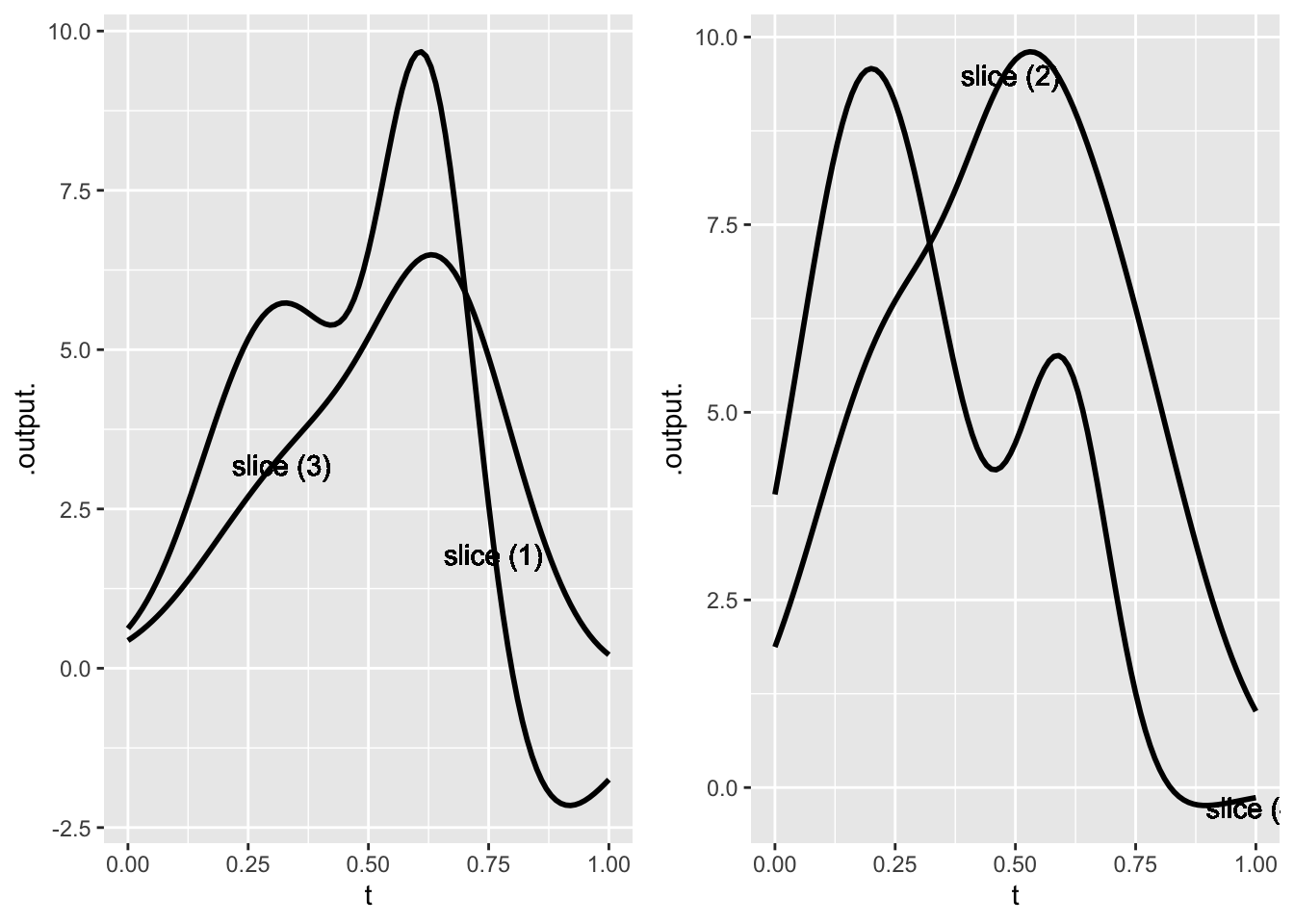
In the slice plots offered in Figure 4, the input \(t\) reflects the position on the slice. At \(t=0\), position is at the leftmost point of the slice, while at \(t=1\) position is at the right terminus of the slice.
- Which color line corresponds to slice 1?
question id: gradient-field-pink-1
- Which color line corresponds to slice 2?
question id: gradient-field-pink-2
- Which color line corresponds to slice 3?
question id: gradient-field-pink-3
- Which color line corresponds to slice 4?
question id: gradient-field-pink-4
Exercise 10 Each of these attempts to define a mathematical function using R leads to an error message. Modify each statement to work properly. (IMPORTANT: You must run the chunk for your answer to be collected. But because the output of makeFun() is being stored under a name, you won’t see any output when you run the chunk. That’s OK.)
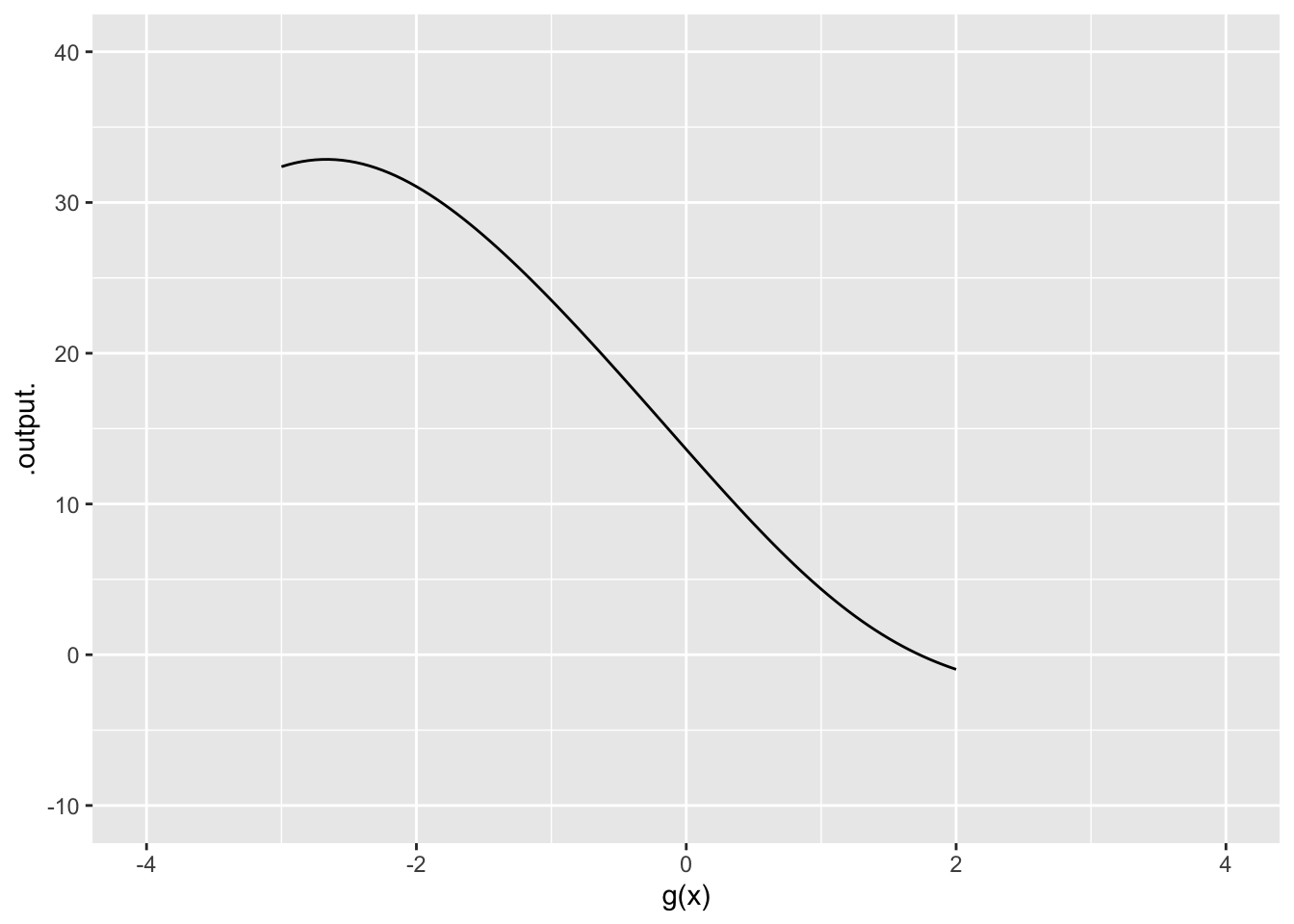
Exercise 11 Consider this graph of a function \(g(x)\):
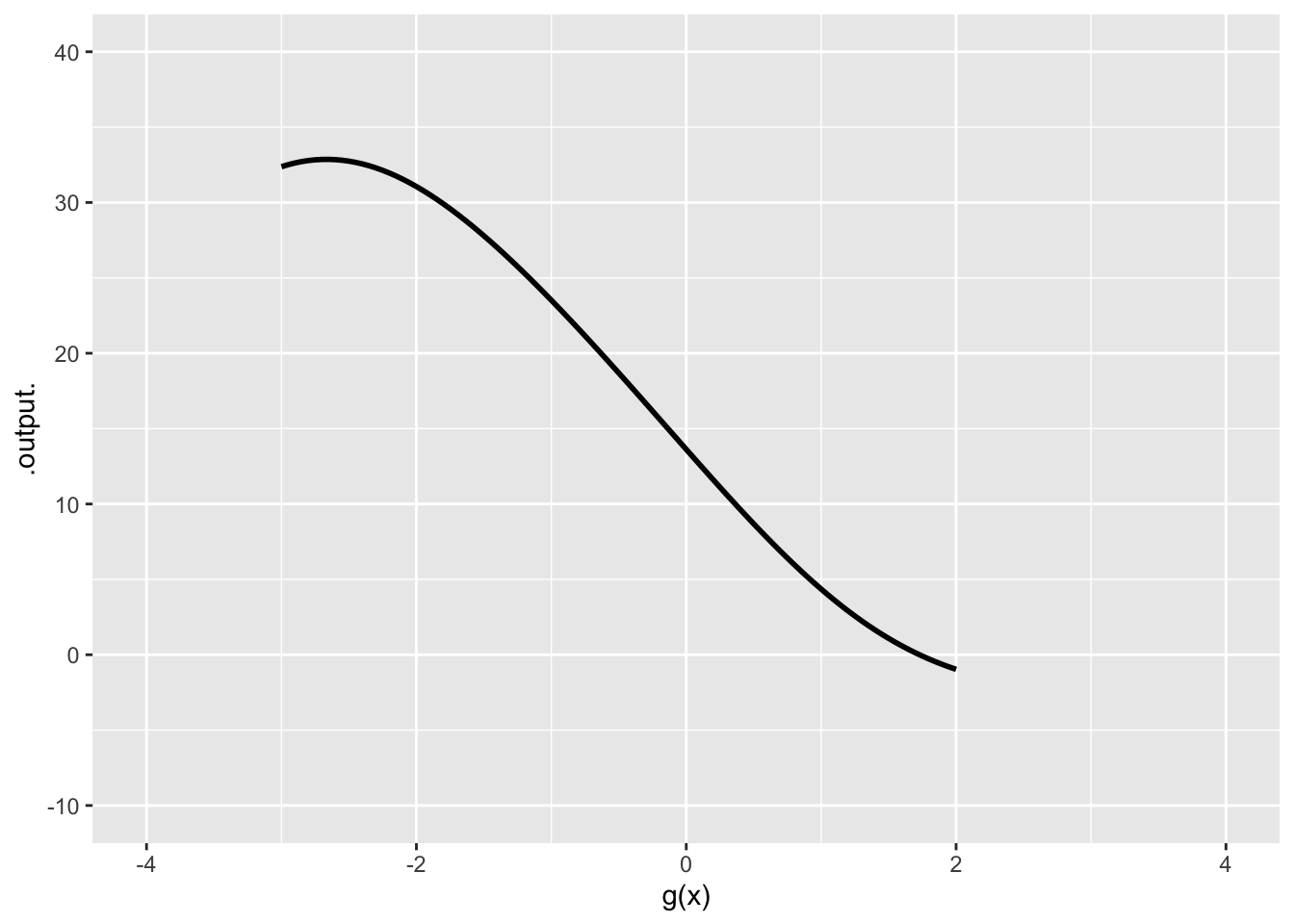
- What is the domain of \(g(x)\)?
\(-\infty < x < \infty\)
\(-3 \leq x \leq 2\)
\(-4 \leq x \leq 4\)
\(-10 \leq g(x) \leq 40\)
\(-1 \leq g(x) \leq 33\)
question id: range-domain-1
- What is the range of \(g(x)\)?
\(-\infty < x < \infty\)
\(-3 \leq x \leq 2\)
\(-4 \leq y \leq 4\)
\(-10 \leq g(x) \leq 40\)
\(-1 \leq g(x) \leq 33\)
question id: range-domain-2
Exercise 12 A triangle consists of three connected line segments: the sides. It has other properties that are related to the sides and each other, for example, the angles between sides, the perimeter, or the area enclosed by the triangle.
Here’s a description of the relationship between the perimeter \(p\) and the lengths of the sides, \(a\), \(b\), \(c\), written in the form of a function: \[p(a,b,c) \equiv a + b + c\ .\] The mathematical expression of the relationship between area \(A\) enclosed by the triangle and the side lengths goes back at least 2000 years to Heron of Alexandria (circa 10–70). As a function, it can be written \[A(a,b,c) \equiv \frac{1}{4}\sqrt{\strut 4a^2b^2-(a^2+b^2-c^2)^2}\ .\]
We cannot readily plot out this function because there are three inputs and one output, and it is impossible to draw in a 4-dimensional space . But we can draw a slice through the 4-dimensional space.
Let’s do that by setting, say, \(a=3\) and looking at the area as a function of the lengths of sides \(b\) and \(c\).
- Not all of the graphics frame is shaded. These are values of \(b\) and \(c\) for which the formula involves a negative quantity in the square root. Thinking about the nature of triangles, why the negative in the square root?
Sides \(a\) and \(b\) are reversed.
\(c\) can never be more than \(b\).
\(c\) can never be more than \(a+b\).
\(c\) can never be more than \(a+b\) or less than \(b-a\).
\(c\) can never be more than \(a+b\) nor less than \(b-a\), nor less than \(a-b\).
question id: seahorse-hear-magnet-1
- Another slice might set \(a = b\), in which case we would be showing the areas of isosceles triangles as in Active R chunk 4
- Draw a contour plot of the area of the triangle when \(a=b\). Referring to your graph, what’s the area of the isosceles triangle with \(a=b=c=4\)?
question id: seahorse-hear-magnet-2
- The R/mosaic command in Active R chunk 4 doesn’t make any reference in the contour plot to an input named
a. Explain what in the command is setting \(a = b\).
Exercise 13 Figure 5 displays a function, but we don’t show you any formula for the function, just the graph.
- Find three points on the surface where \(f(x, y) \approx 15\). (It does not have to be exactly 15, just close.)
- Find a point where \(f(x=2, y) =\approx 8\).
Exercise 14 Often, the specific numerical value at a point is not of primary interest. Instead, we may be interested in how steep the function is at a point, which is indicated by the spacing between contours. When contours are closely spaced, the hillside is steep. Where contours are far apart, the hillside is not steep, perhaps even locally flat.
Another common task for interpreting contour plots is to locate the input pair that is at a local high point or low point: the top of a hill or the bottom of a hollow. Such points are called local argmax or local argmin respectively. The output of the function at a local argmax is called the local maximum; similarly for a local argmin, where the output is called a local minimum.
Answer the following questions For the function shown in Figure 6.
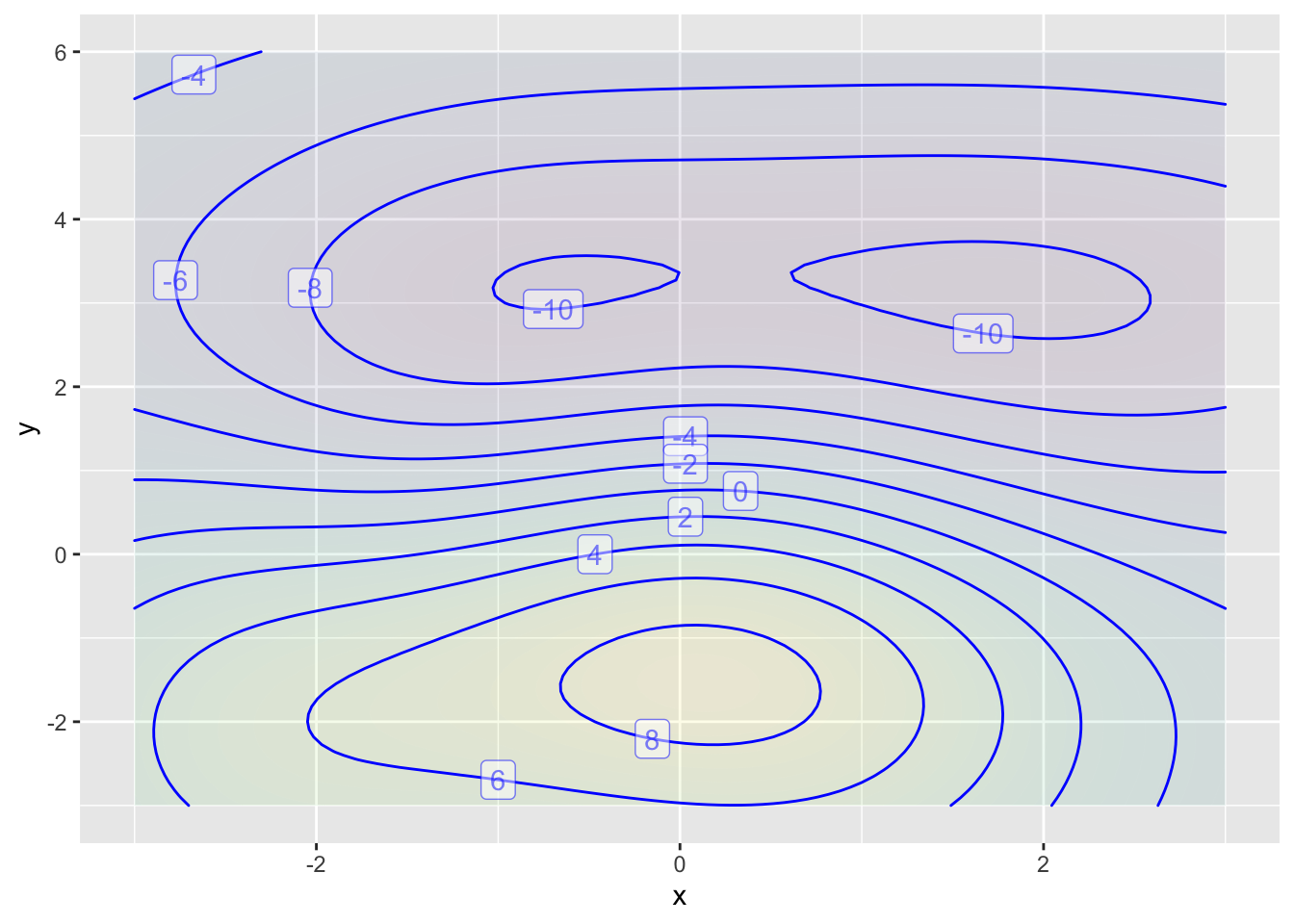
- Find an input coordinate where the function is steepest.
- Find input coordinates for the high and low points of the function .
A function is steepest where contour lines are spaced closely together, that is, where the function output changes a lot with a small change in input. This is true near inputs \((x=0, y=1)\). But notice that steepness involves a direction. Near \((x=0,y=1)\), changing the \(x\) value does not lead to a big change in output, but a small change in the value of \(y\) leads to a big change in output. In other words, the function is steep in the y-direction but not in the x-direction.
The highest output value explicitly marked in the graph is 8. We can imagine from the shapes of the contours surrounding the 8 contour that the function reaches a peak somewhere in the middle of the region enclosed by the 8 contour, near the input coordinate \((x=0, y=-1.5)\).
Similarly, the lowest output value marked is -10. In the middle of the area enclosed by the -10 contour is a local low point. That there are two such regions, one centered near input coordinate \((x=-0.5, y=3.3)\), the other at \((x=1.5, y=3.1)\).
Exercise 15 Consider this interactive contour plot:
- Find a value for the (x, y) inputs where the function output is about -0.35.
- Find a value for the (x, y) inputs where the function output is about 0.9.
One contour goes through the input A=(x=1.53, y=1.59). The neighboring contour goes through B=(x=1.53, y=0.90).
- What is the function output half-way between these two points, at input C=(x=1.53, y=1.25)?
- How does the output at C relate to the output at A and B?
- Choose one of the contours and track the output value (called “z” by the display) as you move the cursor along that contour. What pattern do you see in the output?
Exercise 16 The US National Weather Service provides this graphic for calculating the “heat index.” Source link The output is the heat index, shown both quantitatively (the labels on the contours) and with color.
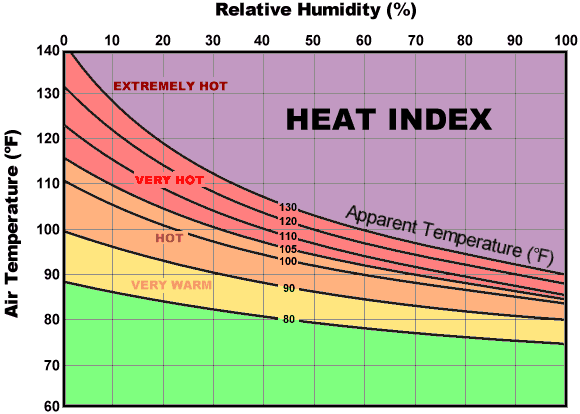 {width = “70%”}
{width = “70%”}
- How many input variables are there?
question id: lion-break-rug-1
- What’s the function output when air temperature is 90 F and humidity is 50%? (Pick the closest value.)
question id: lion-break-rug-2
- True or false: Holding humidity constant, as the air temperature rises, the heat index also increases.
question id: lion-break-rug-3
- True or false: Holding air temperature constant, as humidity rises the heat index also rises.
question id: lion-break-rug-4
- True or false: Heat index increases with temperature at a different rate when the humidity is low compared to when the humidity is high.
question id: lion-break-rug-5
- True or false: Heat index increases with temperature most rapidly when the humidity is low.
question id: lion-break-rug-6
- Consider this statement: “When the air temperature is 102 F and the relative humidity is 77%, the wet-bulb temperature is about 95 F.” Is “heat index” the same as “wet-bulb temperature?”
question id: lion-break-rug-7
Exercise 17 IN-CLASS ACTIVITY
Using the blank grids provided, draw (by hand) a slice plot along the path indicated.
- a slice plot of f() along the slice y = 0.
- a slice plot of f() along the slice x = 0.5
Exercise 18 In-class activity
There are nine pattern-book functions: constant, identity, square, reciprocal, sinusoid, exponential, logarithm, gaussian, sigmoid.
On a piece of paper, sketch from memory a graph of each of the pattern-book functions.
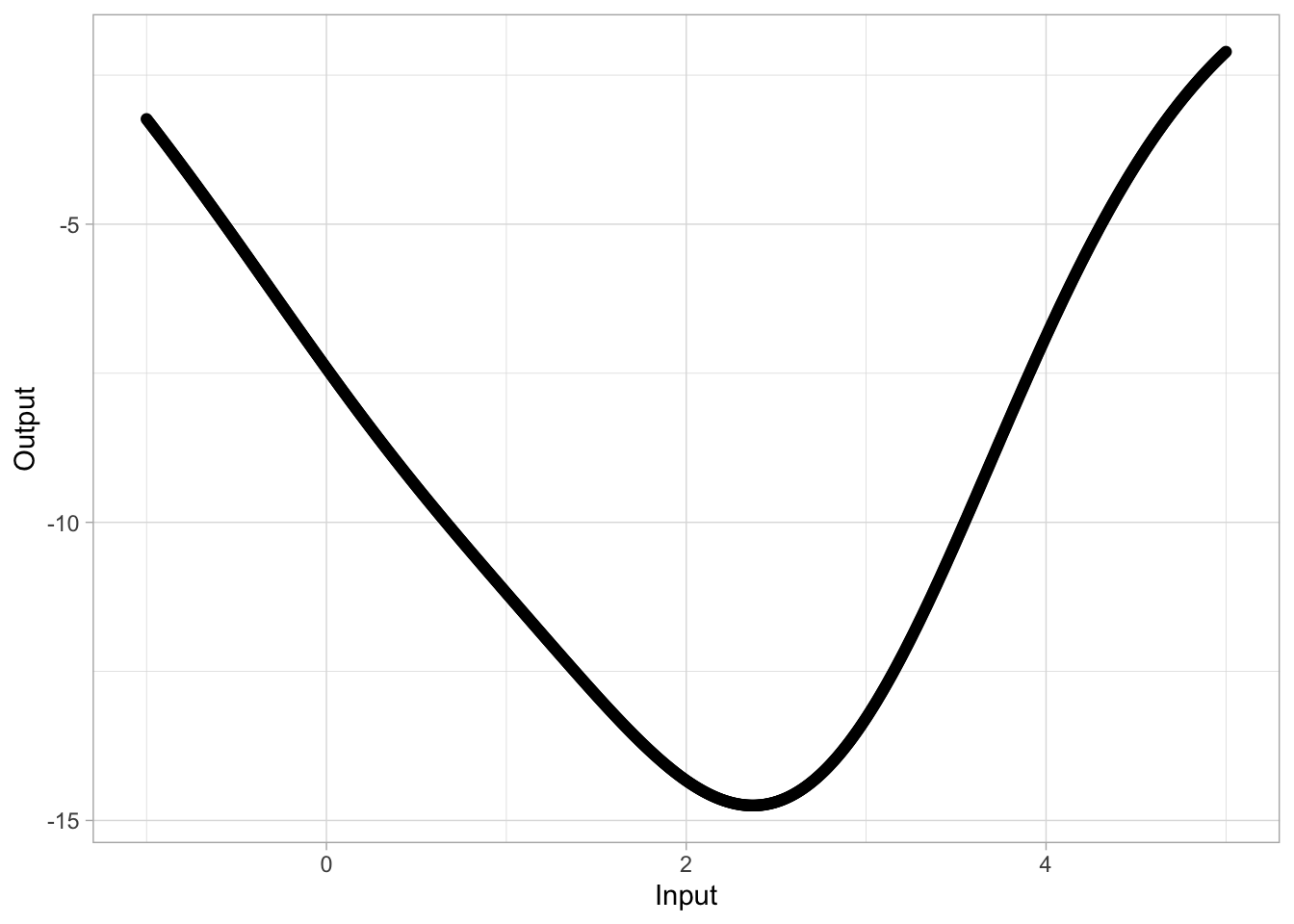
Exercise 19 For the function in Figure 7, find the output values for each of these inputs. Your answers will necessarily be approximate, but be as close as feasible.
| Input | Output |
|---|---|
| -1 | |
| 0 | |
| 3 | |
| 5 |
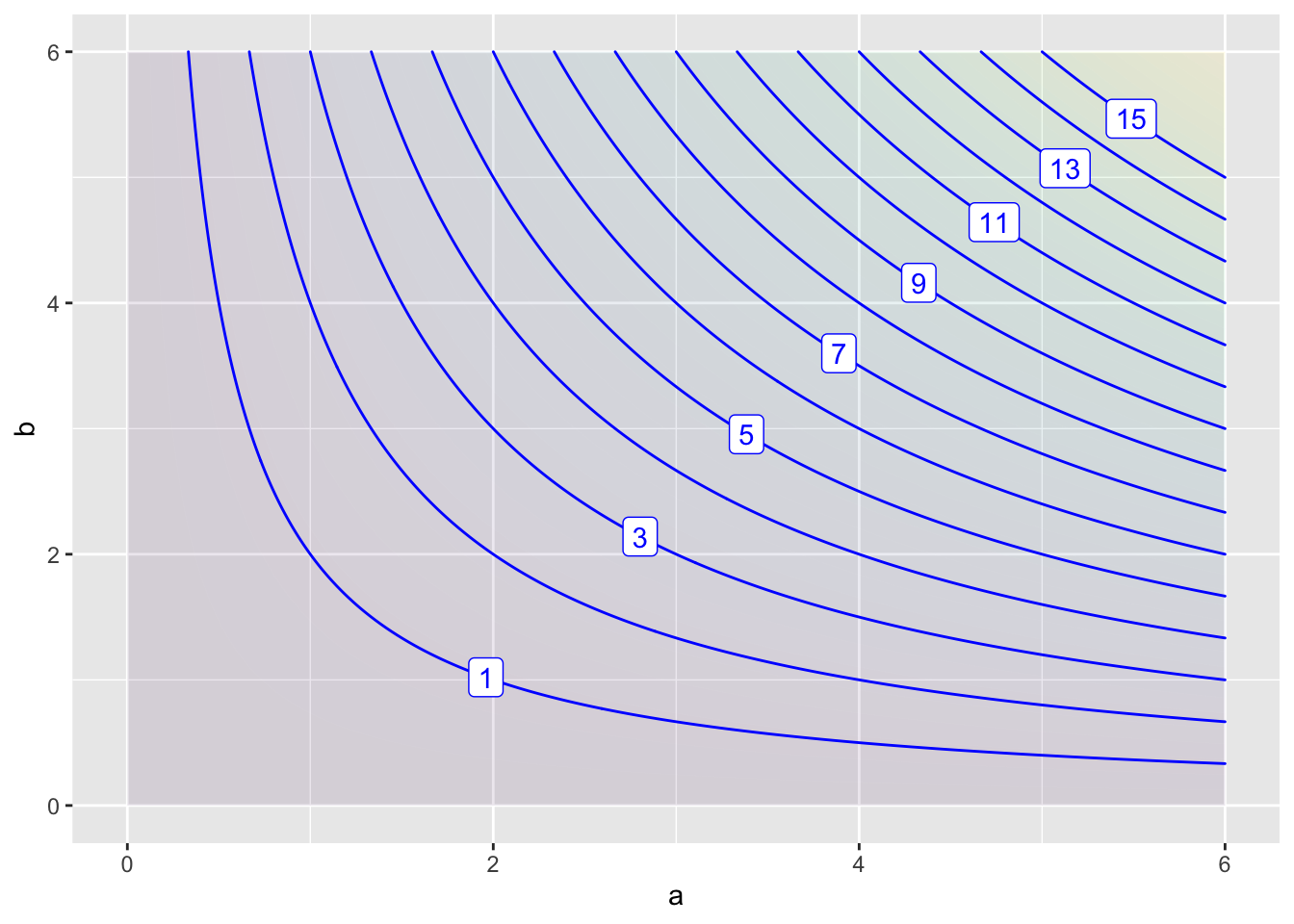
Exercise 20 The area of a triangle is a function of the lengths of the three sides.
\[\text{area}(a,b,c) \equiv \frac{1}{4}\sqrt{\strut 4a^2b^2-(a^2+b^2-c^2)^2}\ .\]
There are three inputs to area(), but a contour or surface plot can represent at most two of them. One possibility is to set one of the inputs to a specific value and represent each of the two remaining inputs as one coordinate axis. For instance, the following plot shows area(a, b, c=4): the area of triangles one side of which has length 4.
Note: Make sure to run Active R chunk 5 before trying Active R chunk 6.
- How can you tell from the command to make the contour plot that one of the sides is being fixed at length 4.
This was specified in the definition of the area() function.
The domain of the plot is restricted to \(a = 4\).
An argument to area() in the plot-making command has been specified by 4.
question id: cheetah-lay-roof-a
- According to Active R chunk 6, what is the area of an equilateral triangle each of whose sides has length 4?
question id: cheetah-lay-roof-b
- From the contour plot, find the a & b side lengths for 3 different triangles, each of which has area 5. (Remember, all triangles in the graphic have side c with length 4.)
- To judge from the output of Active R chunk 6, how many different triangles are there with \(c=4\) and area 3?
question id: cheetah-lay-roof-d
- The interval of the \((a, b)\) space shown in the plot is the square region \(0 \leq a \leq 6\) and \(0 \leq b \leq 6\). Yet there are empty places not marked with any output value. Why? (Hint: What’s the smallest possible area for a triangle?)
- The input space for the area function is three dimensional. In the previous plot we took a planar slice of that space with \(c=4\). Figure 8 shows a different type of slice, the one that includes only right triangles, that is triangles where \(c=a^2 + b^2\).
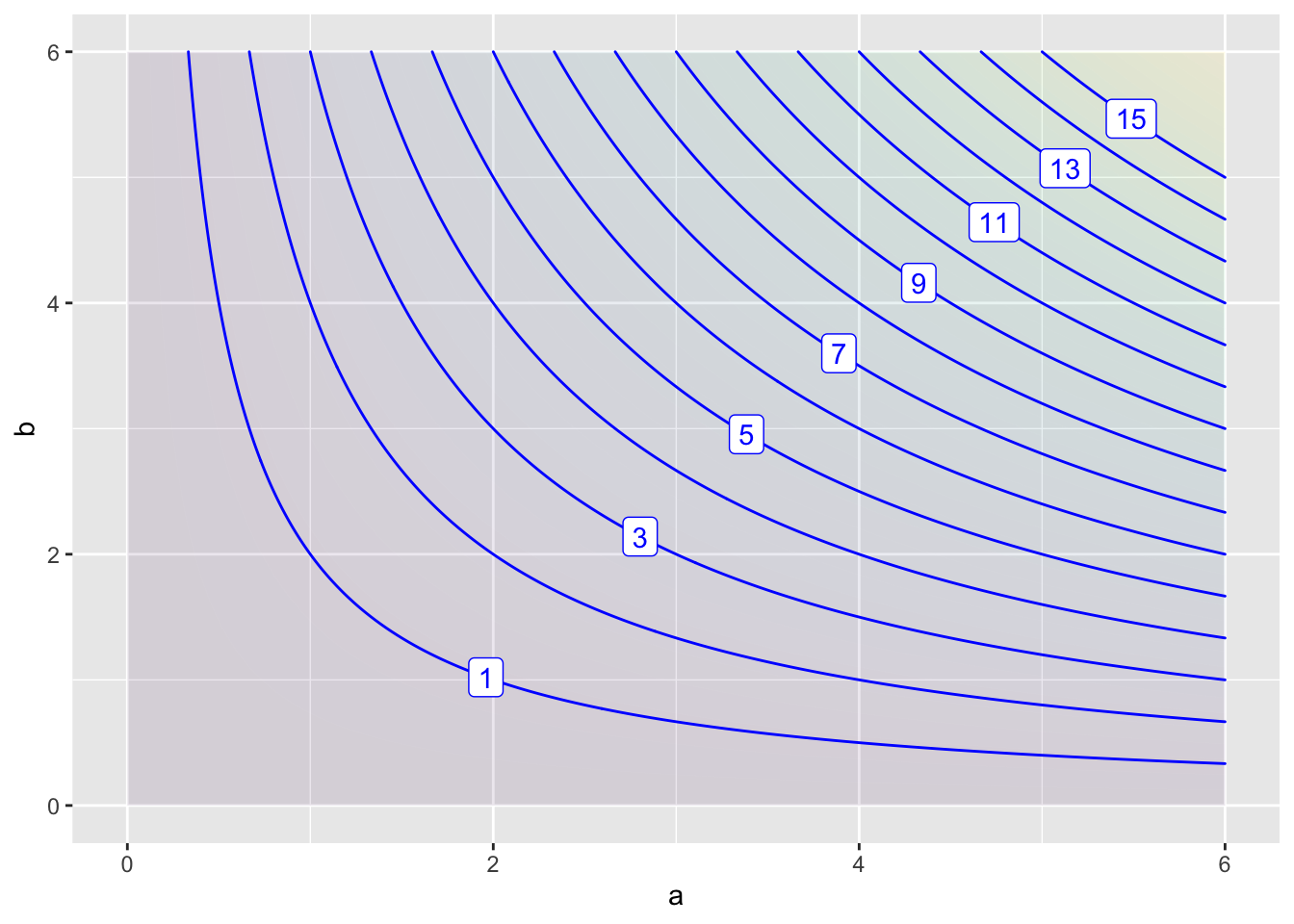
Figure 8 shows the areas of right triangles with side lengths a and b. For right triangles, you can compute the length of side c from the lengths of sides a and b, finding a formula based on the well-known Pythagorean Theorem \(a^2 + b^2 = c^2\)
- Fill in the blank in Active R chunk 7 to reproduce Figure 8.