Chap 28 Exercises

\[ \newcommand{\dnorm}{\text{dnorm}} \newcommand{\pnorm}{\text{pnorm}} \newcommand{\recip}{\text{recip}} \]

Exercise 1 Note: The radio-button multiple choice questions don’t allow us to display a column vector as such. Instead, we use the notation involving a superscript T. For instance, \((2, -3)^T\) is a column vector which we would ordinarily write \(\left(\begin{array}{c}2\\-3\end{array}\right)\) A vector written like \((2, -3)\), without the \(^T\), is a row vector.

Suppose \[\vec{\mathbf{u}} \equiv \left(\begin{array}{c}2\\-3\end{array}\right) \ \ \hbox{and}\ \ \vec{\mathbf{v}} \equiv \left(\begin{array}{c}4\\1\end{array}\right)\] Compute the following linear combinations (arithmetically) …

  1. \(- \vec{\mathbf{u}} -8 \vec{\mathbf{v}}\)

\((-34, -5)^T\)

\((-34, -5)\)

\((-34, 15)\)

\((34, 15)^T\)

Invalid combination

question id: beech-iron-clock-1

  1. \(2.1 \vec{\mathbf{u}} -1.3 \vec{\mathbf{v}}\)

\((-1, -7.6)^T\)

\((0.8)\)

\((-1, -7.6)\)

\((2.1, -1.3)^T\)

Invalid combination

question id: beech-iron-clock-2

  1. \(-0.5 \vec{\mathbf{u}} + 3.2 \vec{\mathbf{v}}\)

\((11.8, 4.7)^T\)

\((2.7)\)

\((13.8, 1.7)\)

\((34, 16)^T\)

Invalid combination

question id: beech-iron-clock-3

  1. \(7 \vec{\mathbf{u}} + 5 \vec{\mathbf{v}}\)

\((34, -16)^T\)

\((32, -14)^T\)

\((34, -14)^T\)

\((32, -16)^T\)

Invalid combination

question id: beech-iron-clock-4

Exercise 2 Here are some vectors to use in answering the following questions.

\[\vec{u} \equiv \left[\begin{array}{r} -100\\\ 98\\\ 9\\ -81\\\ 90\end{array}\right]\ \ \ \vec{v} \equiv \left[\begin{array}{r}\ 21\\\ 37\\\ 93\\ -41\\ -93\end{array}\right]\ \ \ \vec{w} \equiv \left[\begin{array}{r} -97\\ -11\\\ 33\\ -49\\\ 91\end{array}\right]\]

Calculate the length of each of these vectors in the corresponding interactive R chunk.

  1.         \(2 \vec{u}\)
  1.       \(- 2 \vec{u}\)
  1.         \(4 \vec{u}\)
  1.         \(17 \vec{v}\)
  1.      \(- 1.5 \vec{w}\)

Exercise 3 Using R/mosaic and the %dot% and sqrt() functions, calculate the length of each of these vectors:

  1. \(\vec{u} \equiv \left[\begin{array}{r}\ 35\\ -93\\ -99\end{array}\right]\)
  1. \(\vec{v} \equiv \left[\begin{array}{r} -59\\\ 41\\ -41\end{array}\right]\)
  1. \(\vec{w} \equiv \left[\begin{array}{r} -76\\ -71\\ -48\end{array}\right]\)
  1. \(\vec{x} \equiv \left[\begin{array}{r} -96\\\ 83\\\ 35\end{array}\right]\)

Exercise 4 Consider this set of vectors

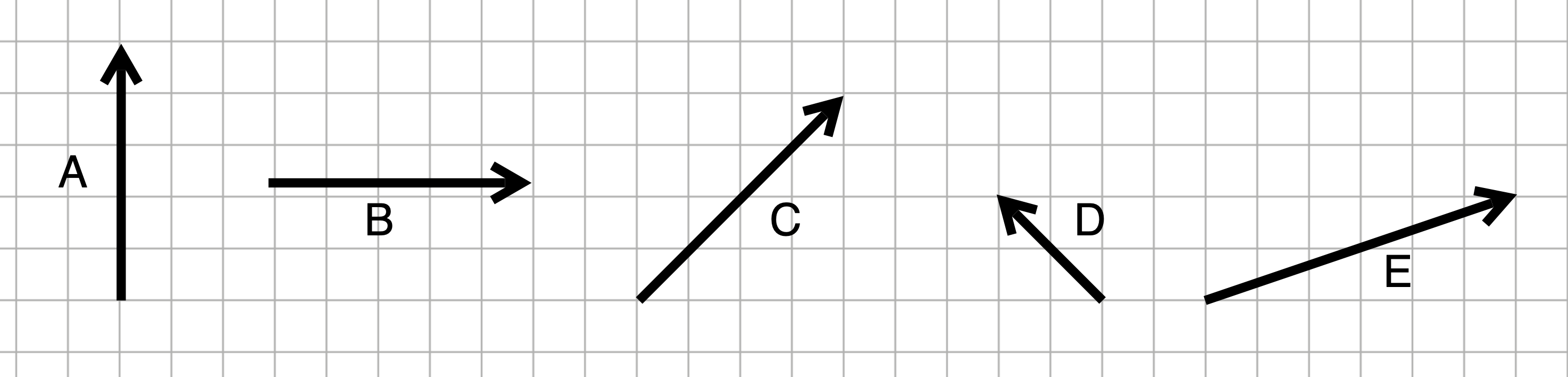
Figure 1: Vectors to use for this exercise
  1. Find the lengths of each of these vectors. Assume that the vectors begin and end exactly on the graph-paper intersections.

Which one of these is not a length of the vectors in Figure 1?

2       4       5       6      

question id: girl-send-scarf-1

  1. Two pairs of vectors in this set are orthogonal within each pair. Which one of these is not one of those pairs?
A and B       B and C       C and D       All of these are orthogonal pairs.      

question id: girl-send-scarf-2

  1. Just using your eye, say whether the dot product between every pair of vectors is positive, zero, or negative.
  1. A & B
positive       zero       negative      

question id: girl-send-scarf-c1

  1. A & C
positive       zero       negative      

question id: girl-send-scarf-c2

  1. A & D (hover to see Figure 1 again.)
positive       zero       negative      

question id: girl-send-scarf-c3

  1. A & E
positive       zero       negative      

question id: girl-send-scarf-c4

  1. B & C (hover to see Figure 1 again.)
positive       zero       negative      

question id: girl-send-scarf-c5

  1. B & D
positive       zero       negative      

question id: girl-send-scarf-c6

  1. B & E
positive       zero       negative      

question id: girl-send-scarf-c7

  1. C & D (hover to see Figure 1 again.)
positive       zero       negative      

question id: girl-send-scarf-c8

  1. C & E
positive       zero       negative      

question id: girl-send-scarf-c9

  1. D & E
positive       zero       negative      

question id: girl-send-scarf-c10

Exercise 5 Consider this vector \[\vec{x} \equiv \left[\begin{array}{r}\ 470\\\ 210\\ -430\end{array}\right]\ .\] For each of the following vectors, calculate the scalar multiplier \(\alpha\) such that \(\alpha \vec{x}\) equals the vectors.

Hint: Try componentwise division.

  1. \(\vec{a} \equiv \left[\begin{array}{r}\ 282\\\ 126\\ -258\end{array}\right]\)
1       2       3       4       6       8       10       12       14       No such multiplier      

question id: tiger-run-futon-1

  1. \(\vec{b} \equiv \left[\begin{array}{r} -376\\ -169\\\ 344\end{array}\right]\)
1       2       3       4       6       8       10       12       14       No such multiplier      

question id: tiger-run-futon-2

  1. \(\vec{c} \equiv \left[\begin{array}{r}\ 752\\\ 336\\ -688\end{array}\right]\)
1       2       3       4       6       8       10       12       14       No such multiplier      

question id: tiger-run-futon-3

  1. \(\vec{d} \equiv \left[\begin{array}{r} -1128\\ -504\\\ 1032\end{array}\right]\)
1       2       3       4       6       8       10       12       14       No such multiplier      

question id: tiger-run-futon-4

Exercise 6 Here are four vectors.

\(\vec{u} \equiv \left[\begin{array}{r}\ 18\\\ 79\\\ 33\\ -41\end{array}\right]\ \ \ \) \(\vec{v} \equiv \left[\begin{array}{r} -35\\ -62\\ -32\\ -7\end{array}\right]\ \ \ \) \(\vec{w} \equiv \left[\begin{array}{r} -44\\\ 81\\\ 74\\ -4\end{array}\right]\ \ \ \) \(\vec{x} \equiv \left[\begin{array}{r} -9\\\ 71\\ -69\\\ 33\end{array}\right]\)

Active R chunk 1 is provided for any calculations you need to do.

Active R chunk 1
  1. Which one of the above vectors is orthogonal to this one? \[\vec{z} \equiv \left[\begin{array}{r} -1\\ -10\\\ 11\\ -4\end{array}\right]\]
\(\vec{u}\)       \(\vec{v}\)       \(\vec{w}\)       \(\vec{x}\)       None of them      

question id: kangaroo-have-closet-1

  1. Which one of the above vectors is orthogonal to this one? \[\vec{z} \equiv \left[\begin{array}{r}\ 4\\\ 1\\\ 1\\\ 1\end{array}\right]\]
\(\vec{u}\)       \(\vec{v}\)       \(\vec{w}\)       \(\vec{x}\)       None of them      

question id: kangaroo-have-closet-2

  1. Which one of the above vectors is almost exactly orthogonal to this one? \[\vec{z} \equiv \left[\begin{array}{r} -1\\ -2\\\ 1.3333333\\\ 3\end{array}\right]\]
\(\vec{u}\)       \(\vec{v}\)       \(\vec{w}\)       \(\vec{x}\)       None of them      

question id: kangaroo-have-closet-3

Exercise 7  

  1. One of the following defines correctly a function that calculates the cosine of the angle between two vectors \(\vec{a}\) and \(\vec{b}\). Which is it?

cang <- makeFun((a %dot% b)/ (sqrt(a %dot% b)*sqrt(b %dot% a)) ~ a + b)

cang <- makeFun((a %dot% b)/ ((a %dot% a)*(b %dot% b)) ~ a + b)

cang <- makeFun((a %dot% b)/ (a %dot% a) * (b %dot% b) ~ a + b)

cang <- makeFun((a %dot% b)/ (sqrt(a %dot% a)*sqrt(b %dot% b)) ~ a + b)

cang <- makeFun((a %dot% a)/ (sqrt(a %dot% a)*sqrt(b %dot% b)) ~ a + b)

question id: lamb-throw-candy-1

  1. Calculate the cosine of the angle between this vector \[\vec{z} \equiv \left[\begin{array}{r} -1\\ -10\\\ 20\\\ 5\end{array}\right]\] and each of the following vectors:

\(\vec{u} \equiv \left[\begin{array}{r}\ 99\\\ 35\\ -25\\\ 92\end{array}\right]\ \ \ \vec{v} \equiv \left[\begin{array}{r} -49\\ -92\\\ 84\\ -65\end{array}\right]\ \ \ \vec{w} \equiv \left[\begin{array}{r} -13\\ -39\\ -55\\\ 65\end{array}\right]\ \ \ \vec{x} \equiv \left[\begin{array}{r} -35\\\ 73\\\ 33\\\ 14\end{array}\right]\)

Active R chunk 2
  1. What is the cosine of the angle between \(\vec{z}\) and \(\vec{w}\)?
0.01723633       -0.1715463       0.6809192       -0.1503336       None of these      

question id: lamb-throw-candy-2

Use Active R chunk 3 to translate each of the cosines from part (2) into degrees of the angle. (Round to the nearest degree.)

Active R chunk 3
  1. What is the angle (in degrees) between \(\vec{v}\) and \(\vec{z}\)?
1\(^\circ\)       15\(^\circ\)       23\(^\circ\)       40\(^\circ\)       47\(^\circ\)       None of these      

question id: lamb-throw-candy-3

Exercise 8 Here are several vectors:

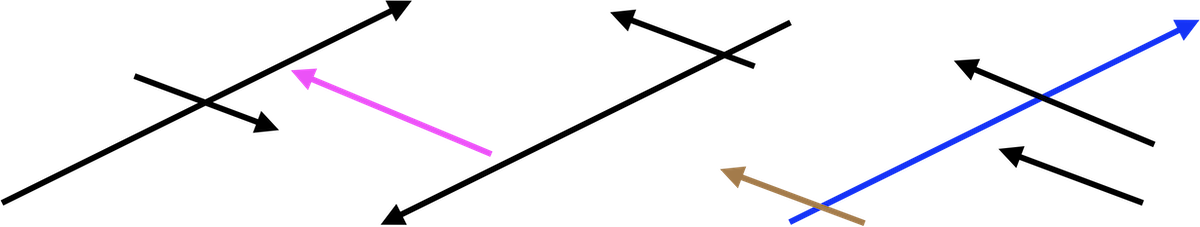
  1. Remembering that mathematical vectors have only two properties—length and direction—how many mathematically different vectors are being shown.
Answer

Five. Color is not a property of a mathematical vector. Orientation, however, is.

  1. Measure the length of each vector. (Hint: Use a ruler! You can round to the nearest millimeter.)

  2. Find the included angle between the \(\color{blue}{\text{blue}}\) and \(\color{brown}{\text{brown}}\) vectors. (Your answer should be correct to within \(\pm 15^\circ\).)

Answer

About 135 degrees. Note that the orientation makes a difference. The angle is measured with the vectors placed tail to tail.

  1. Find the included angle between the \(\color{magenta}{\text{magenta}}\) and \(\color{blue}{\text{blue}}\) vectors.
Answer

Magenta points in the same direction as brown, so the answer is the same as in the previous question.

  1. Find the included angle between 0.7 times the \(\color{blue}{\text{blue}}\) vector and -11.3 times the \(\color{brown}{\text{brown}}\).
Answer

The scaling does not matter except that the negative sign for the brown vector means that its orientation will be reversed. This means that the included angle will be 45 degrees, not 135 degrees as in the previous two questions.

Exercise 9 Collision course?

Consider the diagram showing two straight-line tracks, a dot on each track, and a vector.

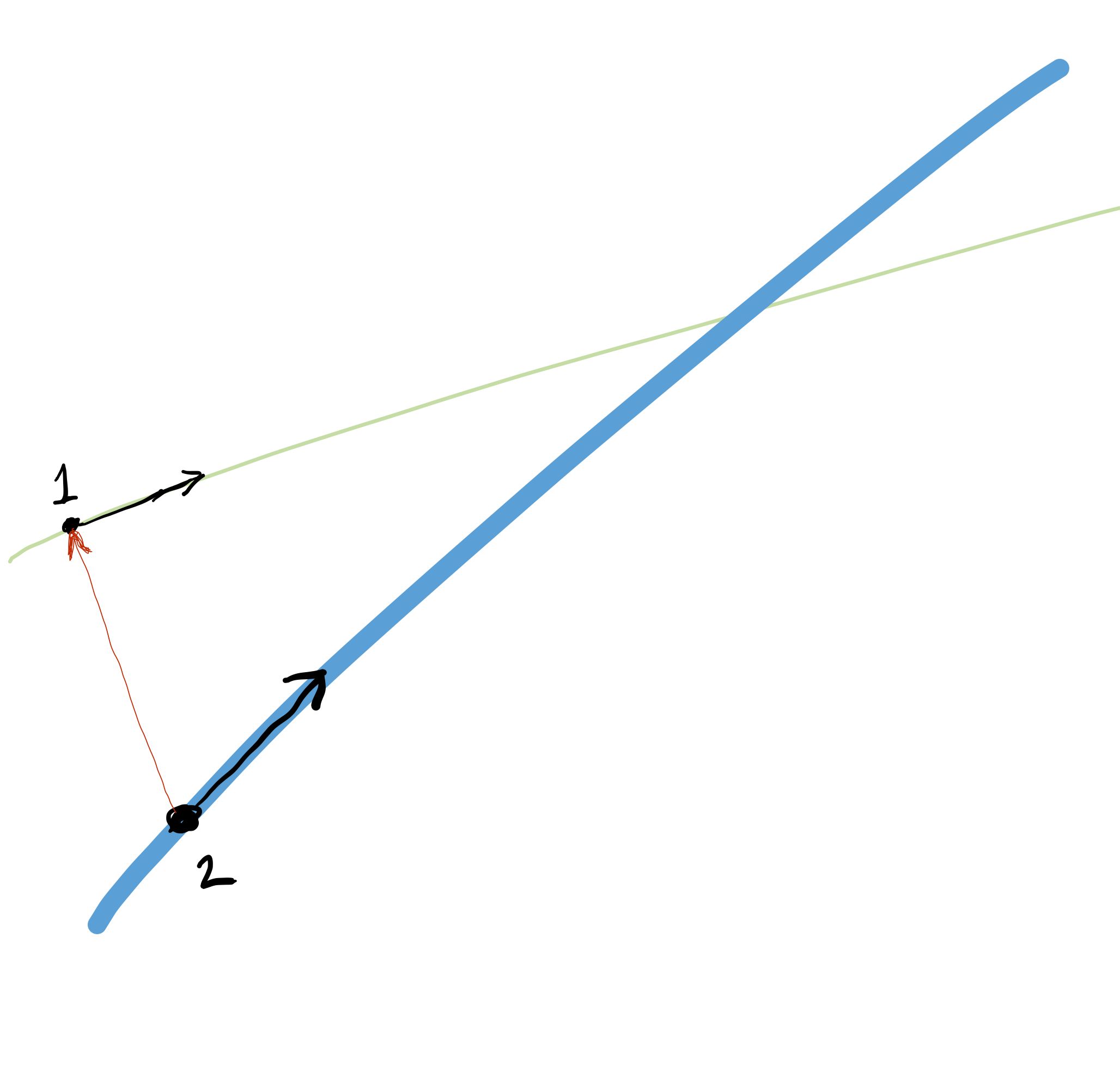
Let’s imagine that dot 1 is an aircraft and that the black vector attached to it is the aircraft’s velocity. We will call this \(\vec{v}_1\), Similarly for dot 2, where the velocity vector will be called \(\vec{v}_2\).

There is a third vector drawn in red: the difference in position of the two aircraft at the exact moment depicted in the drawing.

The question we want to address is whether the aircraft are on a collision course. Obviously, the two courses cross. So we know that the two aircraft will cross the same point. For a collision, the aircraft have to cross that point at the same time.

Copy over the drawing to your own piece of paper. You don’t need to get the vectors and positions exactly right; any reasonable approximation will do.

Now you will do visual vector addition and subtraction to answer the collision question.

  1. The relative velocity of the two planes is the difference between their velocities. Subtract \(\vec{v}_2\) from \(\vec{v}_1\) and draw the resulting vector. Pay attention to both the length and direction of the relative velocity.

  2. The displacement between the two planes is the red vector: the position of dot 2 subtracted from dot 1. Compare the directions of the relative velocity vector and the displacement vector. If they are aligned, then the planes are on a collision course.

  3. In the picture as drawn, the relative velocity vector and the displacement vector are not aligned. Figure out how much you would need to change the length of \(\vec{v}_2\) so that the relative velocity does align with the displacement. (Keep the direction the same.) Draw this new vector and label it “vector for intercept.”

  4. In (3) you changed the length of \(\vec{v}_2\) keeping the direction the same. Now you will keep \(\vec{v}_2\) at the original length, but change its direction so that the new relative velocity is aligned with the displacement vector.

Items (3) and (4) are two different ways of designing an intercept of plane 1 by plane 2.

Bonus) You can figure out how long it takes for each plane to reach the intersection point by finding out how many multiples of the velocity vector will cover the line segment between the plane’s position and the intersection point. For example, in the original drawing \(4 \vec{v}_1\) will bring the plane to the intersection point, so it takes 4 “time units” for the plane to reach the point. (What is the time unit? If velocity is in miles/hour, then the time unit is hours. If the velocity is in feet/second, then the time unit is seconds.) Your task: Figure out where aircraft 2 will be in 4 time units. This will tell you the separation between aircraft 2 and aircraft 1 when 1 reaches the intersection point. Draw and label this vector.

Exercise 10 In physics and engineering, there is a very important operation called the cross product and written \(\vec{u}\times\vec{v}\). The operation is only defined for vectors in 3-dimensional space. The output of the cross product is another 3-dimensional vector which can be calculated arithmetically as:

\[\left(\begin{array}{c}a\\b\\c\end{array}\right) \times \left(\begin{array}{c}e\\f\\g\end{array}\right) \equiv \left(\begin{array}{c}b\, g - c\, f\\c\, e - a\, g\\a\, f - b\, e\end{array}\right)\]

Make up coordinates for two three-dimensional vectors \(\vec{u}\) and \(\vec{v}\) that point in different directions.

Calculate the cross product \(\vec{w} \equiv \vec{u} \times \vec{v}\).

  1. Find the angle between \(\vec{w}\) and \(\vec{u}\).
  2. Find the angle between \(\vec{w}\) and \(\vec{v}\).

Other than this brief description, we will not use cross products at all in this course. But keep them in mind for your upcoming physics and engineering courses.

Activities

Exercise 11 Collision course?

Consider the diagram showing two straight-line tracks, a dot on each track, and a vector.

Let’s imagine that dot 1 is an aircraft and that the black vector attached to it is the aircraft’s velocity. We will call this \(\vec{v}_1\), Similarly for dot 2, where the velocity vector will be called \(\vec{v}_2\).

There is a third vector drawn in red: the difference in position of the two aircraft at the exact moment depicted in the drawing.

The question we want to address is whether the aircraft are on a collision course. Obviously, the two courses cross. So we know that the two aircraft will cross the same point. For a collision, the aircraft have to cross that point at the same time.

Copy over the drawing to your own piece of paper. You don’t need to get the vectors and positions exactly right; any reasonable approximation will do.

Now you will do visual vector addition and subtraction to answer the collision question.

  1. The relative velocity of the two planes is the difference between their velocities. Subtract \(\vec{v}_2\) from \(\vec{v}_1\) and draw the resulting vector. Pay attention to both the length and direction of the relative velocity.

  2. The displacement between the two planes is the red vector: the position of dot 2 subtracted from dot 1. Compare the directions of the relative velocity vector and the displacement vector. If they are aligned, then the planes are on a collision course.

  3. In the picture as drawn, the relative velocity vector and the displacement vector are not aligned. Figure out how much you would need to change the length of \(\vec{v}_2\) so that the relative velocity does align with the displacement. (Keep the direction the same.) Draw this new vector and label it “vector for intercept.”

  4. In (3) you changed the length of \(\vec{v}_2\) keeping the direction the same. Now you will keep \(\vec{v}_2\) at the original length, but change its direction so that the new relative velocity is aligned with the displacement vector.

Items (3) and (4) are two different ways of designing an intercept of plane 1 by plane 2.

Bonus) You can figure out how long it takes for each plane to reach the intersection point by finding out how many multiples of the velocity vector will cover the line segment between the plane’s position and the intersection point. For example, in the original drawing \(4 \vec{v}_1\) will bring the plane to the intersection point, so it takes 4 “time units” for the plane to reach the point. (What is the time unit? If velocity is in miles/hour, then the time unit is hours. If the velocity is in feet/second, then the time unit is seconds.) Your task: Figure out where aircraft 2 will be in 4 time units. This will tell you the separation between aircraft 2 and aircraft 1 when 1 reaches the intersection point. Draw and label this vector.

Exercise 12 Write (or draw) your answers on a sheet of paper. You can do the any calculations you need using Active R chunk 4. Make sure to write column vectors in a correct column format. Use Active R chunk 4 for numerical calculations.

Active R chunk 4
  1. What is \(5.42 \left(\begin{array}{r}7.3\\8.9\\-2.4\end{array}\right)\)?
  2. What is \(-2.67 \left(\begin{array}{r}-19.34\\0.23\\14.82\end{array}\right)\)?
  3. Draw a vector of your own choice. Next to it, draw the vector which is 2.5 times your vector.
  4. Take your original vector from (c) and draw the vector which is -3 times it.
  5. Write down the R code to create a vector named w that is \[\left(\begin{array}{c}2\\5\\1\\5\end{array}\right)\]
No answers yet collected