52 Present and future value
Comparison is an important element of human decision making. Often, comparison amounts to translating each of the options at hand into a scalar score. (Recall that a scalar is just an ordinary quantity, e.g. 73 inches. As we get more deeply involved with vectors it will become more important to be perfectly clear when we are talking about a vector and when about a scalar. So we will be using “scalar” a lot.) Scalars are easy to compare; the skill is taught in elementary school. Scalar comparison is completely objective. Putting aside the possibility of error, everyone will agree on which of two numbers is bigger. Importantly, comparison of scalars is transitive, that is if \(a > b\) and \(b > c\) then it is impossible that \(a \leq c\).
The comparison of scalars can be extended to situations where the options available form a continuum and the score for each option \(x\) is represented by a function, \(f(x)\). Chapter 24 and Chapter 50 showed that selecting the highest scoring option is a matter of finding the argmax.
Many decisions involve options that have two or more attributes that are not directly comparable. Expenditure decisions have this flavor: Is it worth the money to buy a more reliable or prettier or more capable version of a product? The techniques of constrained optimization (Chapter 50) provide one useful approach for informing decisions when there are multiple objectives.
Elections are a form of collective decision making. The options—called, of course, “candidates”—have many attributes. Three such attitudes are attitudes toward social policy, toward fiscal policy, and toward foreign policy. Perceived honesty and trustworthiness as well as the ability to influence other decision makers and perceived ability to win the election are other attributes that are considered and balanced against one another. Ultimately the decision is made by condensing the diverse attributes into a single choice for each voter. The election is decided by how many votes the candidate garners. With this number attached to each of the candidates, it is easy to make the decision, \[\text{winner} \equiv\mathop{\text{argmax}}_{i}\left({\large\strut} \text{votes}(\text{candidate}_i)\right)\ .\] There are many voting systems. For instance, sometimes the winner is required to have a majority of votes and, if this is not accomplished, the two highest vote-getting candidates have a run-off. Some jurisdictions have introduced “rank-choice” voting, where each voter can specify a first choice, a second choice, and so on. US federal elections involve a primary system where candidates compete in sub-groups before the groups complete against one another. It is tempting to think that there is a best voting system if only we were clever enough to find one and convince authorities to adopt it. But two mathematical theorems, Arrow’s impossibility theorem and the Gibbard-Satterthwaite theorem demonstrate that this is not the case for any system that involves three or more candidates. All such voting systems potentially create situations where a voter’s sincere interests are best served by an insincere, tactical vote choice. A corollary is that voters can be tricked into making a sincere choice that violates their interests.
This chapter is about a very common situation where there are multiple attributes that need to be condensed into a single score. The setting is simple: money. The question is how to condense a future income/expense stream—a function of time—into an equivalent value of money in hand at the present. This is called the present value problem. There is a solution to the problem that is widely accepted as valid, just as voting is a hallowed process of social optimization. But like voting, with its multiplicity of possible forms, there is a subtlety that renders the result somewhat arbitrary. This is not a situation where there is a single, mathematically correct answer but rather a mathematical framework for coming to sensible conclusions.
52.1 Present value
People and institutions often have to make decisions about undertakings where the costs and benefits are spread out over time. For instance, a person acquiring an automobile or home is confronted with a large initial outlay. The outlay can be financed by agreeing to pay amounts in the future, often over a span of many years.
Another example: Students today are acutely aware of climate change and the importance of taking preventive or mitigating actions such as discouraging fossil fuel production, investing in renewable sources of energy and the infrastructure for using them effectively, and exploring active measures such as carbon sequestration. The costs and benefits of such actions are spread out over decades, with the costs coming sooner than the benefits. Policy makers are often and perhaps correctly criticized for overvaluing present-day costs and undervaluing benefits that accrue mainly to successive generations. There are many analogous situations on a smaller scale, such as setting Social Security taxes and benefits or the problem of underfunded pension systems and the liability for pension payments deferred to future taxpayers.
The conventional mechanism for condensing an extended time stream of benefits and costs is called discounting. Discounting is based on the logic of financing expenditures via borrowing at interest. For example, credit cards are a familiar mechanism for financing purchases by delaying the payment of money until the future. An expense that is too large to bear is “carried” on a credit card so that it can be paid off as funds become available in the future. This incurs costs due to interest on the credit-card balance. Typical credit-card interest rates are 18-30% per year.
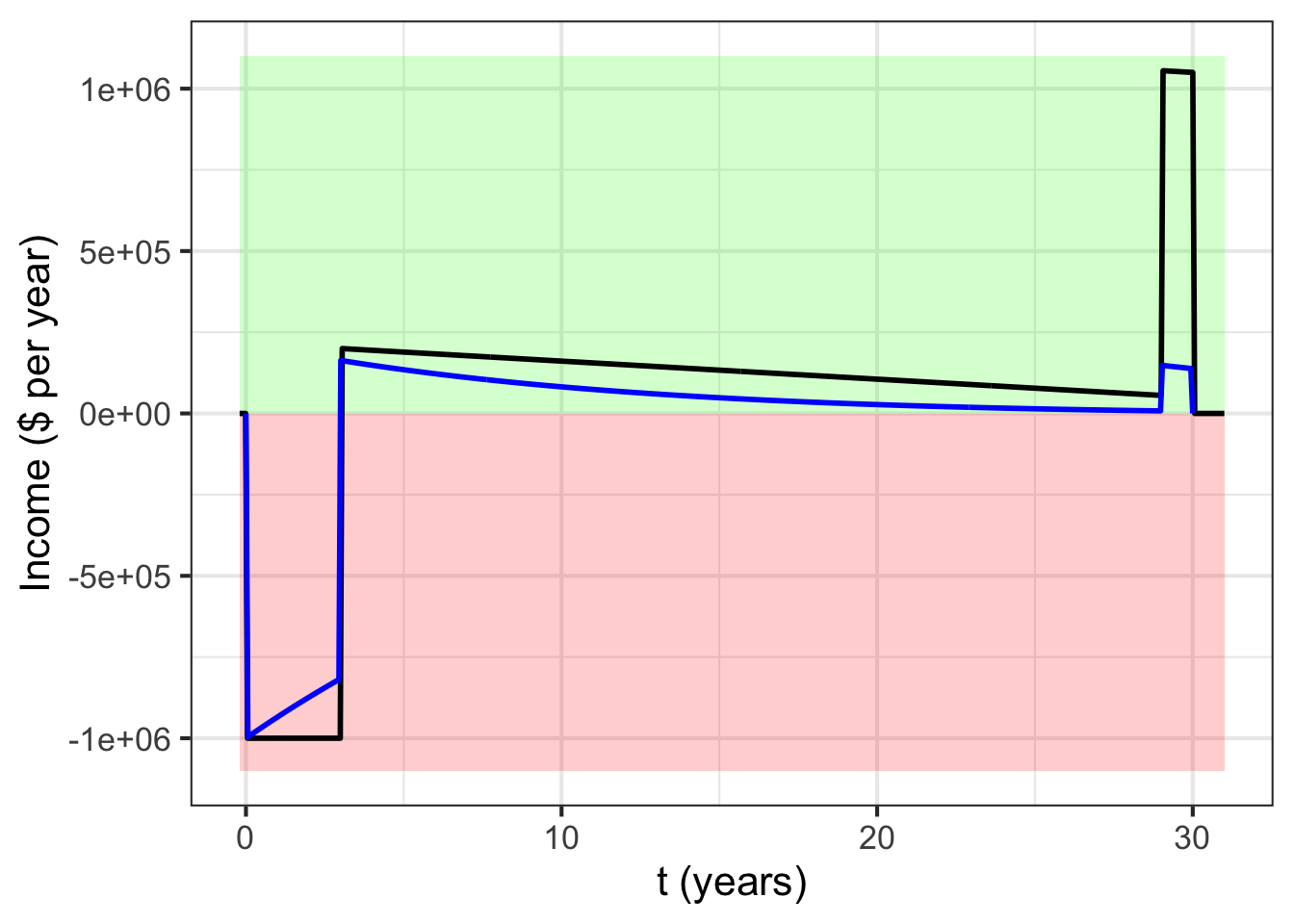
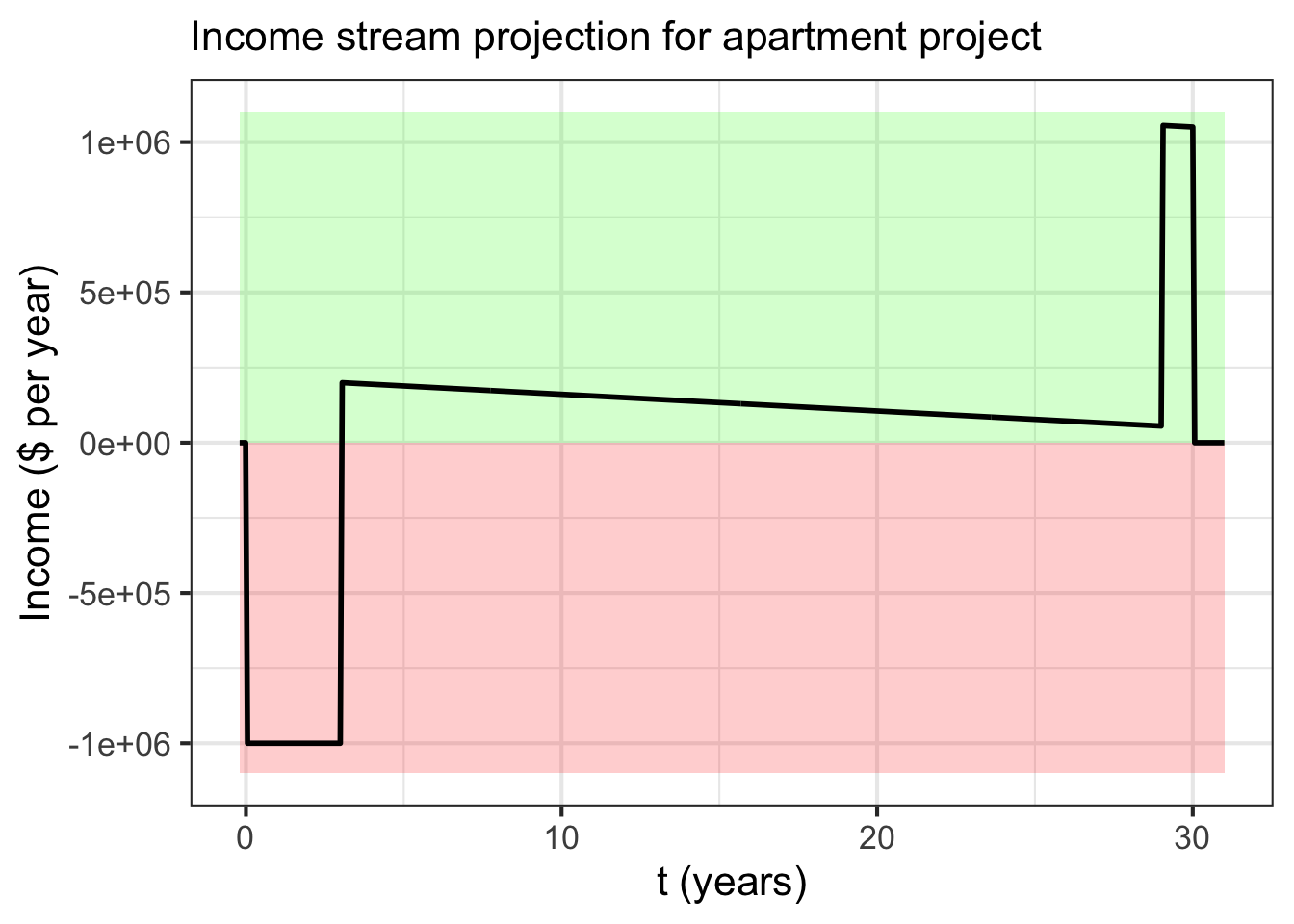
As notation, consider a time stream of income \({\cal M}(t)\), as with the apartment building example. We will call \({\cal M}(t)\) the nominal income stream with the idea that the money in \({\cal M}(t)\) is to be counted at face value. “Face value” is the literal amount of the money. In the case of cash, a $20 bill has a face value of $20 regardless of whether it becomes available today or in 50 years. The word “nominal” refers to the “name” on the bill, for instance $20.
The big conceptual leap is to understand that the present value of income in a future time is less than the same amount of income at the present time. In other words, we discount future money compared to present money. For example, if we decide that an amount of money that becomes available 10 years into the future is worth only half as much as that same amount of money if it were available today, we would be implying a discounting to 50%. In comparison, if that money were available 20 years in the future, it would make sense to discount it by more strongly to, say, 25%.
To represent the discounting to present value as it might vary with the future time horizon, we multiply the nominal income stream \({\cal M}(t)\) by a discounting function \({\cal D} (t)\). The function \({\cal D}(t)\, {\cal M}(t)\) gives the income stream as a present value rather than a nominal value. It is sensible to insist that \({\cal D} (t=0) \equiv 1\) which is merely to say that the present value of money available today is the same as the nominal value.
The net present value (NPV) of a nominal income stream \({\cal M}(t)\) is simply the sum of the stream discounted to the present value. Since we are imagining that the income stream is a function of continuous time, the sum amounts to an integral: \[\text{NPV} \int_\text{now}^\text{forever} {\cal M}(t)\ {\cal D}(t)\, dt\ .\]
52.2 Discounting functions
What should be the shape of the discounting function?
Recall that the purpose of the discounting function is to help us make comparisons between different income streams, that is, between the various options available to an entrepreneur. Each individual can in principle have his or her own, personal discounting function, much as each voter is entirely free to weight the different attributes of the candidates when deciding whom to vote for. As a silly example, a person might decide that money that comes in on a Tuesday is lucky and therefore worth more than Thursday money. We won’t consider such personalized forms further and instead emphasize discounting functions that reflect more standard principles of finance and economics.
As a thought experiment, consider the net present value of an income stream, that is \[\text{NPV}_\text{original} = \int_0^\infty {\cal M}(t)\ {\cal D}(t)\, dt\ .\] Imagine now that it has been proposed to delay the income stream by \(T=10\) years. This new, delayed income stream is \({\cal M}(t-T)\) and also has a net present value: \[\text{NPV}_\text{delayed} = \int_0^\infty {\cal M}(t - T)\ {\cal D}(t)\, dt\ .\] There are at least two other ways to compute \(\text{NPV}_\text{delayed}\) that many people would find intuitively reasonable:
- Simply discount the original NPV to account for it becoming available \(T\) years in the future, that is, \[\text{NPV}_\text{delayed} = {\cal D}(T)\ \text{NPV}_\text{original} = \int_0^\infty {\cal M}(t)\ {\cal D}(T)\ {\cal D}(t)\, dt\ \]
- Apply to \({\cal M}(t)\) a discount that takes into account the \(T\)-year delay. That is:
\[\text{NPV}_\text{delayed} = \int_0^\infty {\cal M}(t)\ {\cal D}(t + T)\, dt\ .\] For (1) and (2) to be the same, we need to restrict the form of \({\cal D}_r(t)\) so that \[{\cal D}(T)\ {\cal D}(t) = {\cal D} (t+T)\ .\] The form of function that satisfies this restriction is the exponential, that is \({\cal D}(t) \equiv e^{kt}\).
52.3 Compound interest
A more down-to-earth derivation of the form of \({\cal D}(t)\) is to look at how financial transactions take place in the everyday world: borrowing at interest. Suppose that a bank proposes to lend you money at an interest rate of \(r\) per year. To receive from the bank one dollar now entails that you pay the bank \(1+r\) dollars at the end of the year.
For this proposition to be attractive to you, the present value of \(1+r\) dollars to be paid in one year must be less than or equal to the present value of one dollar today. In other words, \[{\cal D}_\text{you}(1)\ (1+r) \leq 1\ .\] From the bank’s perspective, the present value of your payment of \((1+r)\) dollars in a year’s time must be greater than one dollar today. That is
\[1 \leq {\cal D}_\text{bank}(1)\ (1+r) \ .\] It is perfectly reasonable for you and the bank to have different discounting functions, just as it is perfectly legitimate for you and another voter to have different opinions about the candidates. It is convenient, though to imagine that the two discounting functions are the same, which will be the case if \[{\cal D}(1) = \frac{1}{1+r}\ .\]
If you were to borrow money for two years, the bank would presumably want to charge more for the loan. A typical practice is to charge compound interest. Compound interest corresponds to treating the loan as having two phases: first, borrow one dollar for a year and owe \(1+r\) dollars at the end of that year. At that point, you will borrow \((1+r)\) dollars at the interest rate \(r\). At the end of year two you will owe \((1+r) (1+r) = (1+r)^2\) dollars. In general, if you were to borrow one dollar for \(t\) years you would owe \((1+r)^t\) dollars. In order for the loan to be attractive to both you and the bank, the discounted value of \((1+r)^t\) should be one dollar: \[{\cal D}(t) = \frac{1}{(1+r)^t} = (1 + r)^{-t}\ .\]
Application area 52.2 Building apartments (2)
Let’s return to the entrepreneur considering the apartment-building project in Application area 52.1.
The entrepreneur goes to the bank with her business plan and financial forecasts. The bank proposes to lend money for the project at an interest rate of 7% per year.
Figure 52.2 shows the income stream discounted at 7% per year. The net present value of the income stream for the apartment project is the accumulation of the discounted income stream: \[\text{NPV}(7\%) = \int_0^{30} (1 + 0.07)^{-t} {\cal M}(t) \ dt \ .\] This works out to be negative $1,095,000. As things stand, the apartment building will be a money pit.
The entrepreneur responds to the bank’s offer with some business jargon. “I’ll have to go back to the drawing board, put the team’s heads together, and see how to get the numbers to work. I’ll circle back with you tomorrow.” This might involve reconsidering her model of the income stream. Perhaps she should have taken into account yearly rent increases. Maybe she can re-negotiate with the city about zoning height restrictions and build a 12-unit building, which will cost $4 million, lowering the cost per apartment?
52.4 Mortgages
A mortgage is a form of loan where you pay back the borrowed amount at a steady rate, month by month. At the end of a specified period, called the term of the mortgage, your have completely discharged the debt.
Suppose you decide to buy a product that costs \(\$\cal P\), say \(\cal P=\) $10,000 for a used car. Let’s say you need the car for your new job, but you don’t have the money. So you borrow it.
Your plan is to pay an amount \(A\) each month for 30 months—the next \(2\,\small\frac{1}{2}\) years. What should that rate be?
You can put the purchase on your credit card at an interest rate of \(r=2\%\) per month. This corresponds to \(k = \ln(1+r) = 0.0198\) per month. The net present value of your payments over 30 months at a rate of \(A\) per month will be
\[\int_0^{30} A {\cal D}_r(t)\, dt = \int_0^{30} e^{-kt} A = -\frac{A}{k} e^{-kt}\left.{\Large\strut}\right|_{t=0}^{30}\] \[=- A \left(\strut \frac{e^{-30k}}{k} - \frac{e^{-0k}}{k} \right)\\ = - A\left(\strut27.88 - 50.50\right) = 22.62 A\]
The loan will be in balance if the net present value of the payments is the same as the amount \({\cal P}\) you borrowed. For this 30-month loan, this amounts to \[22.62 A = {\cal P}\ ,\] from which you can calculate your monthly payment \({\cal A}\). For the $10,000 car loan, your monthly payment will be $10,000/22.62 or $442.09.