12  Adjustment

The phrase “all other things being equal” is a critical qualifier in describing relationships. To illustrate: A simple claim in economics is that a high price for a commodity reduces the demand. For example, increasing the price of gasoline will reduce demand as people avoid unnecessary driving or purchase electric cars. Nevertheless, the claim can be considered obvious only with the qualifier all other things being equal. For instance, the fuel price might have increased because a holiday weekend and the attendant vacation travel has increased the demand for gasoline. Thus, higher gasoline prices may be associated with higher demand unless holding constant other variables such as vacationing.

The Latin equivalent of “all other things being equal” is sometimes used in economics: “ceteris paribus”. The economics claim would be, “higher prices are associated with lower demand, ceteris paribus.”

Although the phrase “all other things being equal” has a logical simplicity, it is impractical to implement “all.” So instead of the blanket “all other things,” it is helpful to consider just “some other things” to be held constant, being explicit about what those things are. Other phrases along the same lines are “adjusting for …,” “taking into account …,” and “controlling for ….”

Groupwise adjustment

“Life expectancy” is a statistical summary familiar to many readers. Life expectancy is often the evidence provided in debates about healthcare policies or environmental conditions. For instance, consider this pull-quote from the Our World in Data website:

“Americans have a lower life expectancy than people in other rich countries despite paying much more for healthcare.”

Table 12.1: Life expectancy at birth for several countries and territories. Source
Country Female Male
Japan 87.6 84.5
Spain 86.2 80.3
Canada 84.7 80.6
United States 80.9 76.0
Bolivia 74.0 71.0
Russia 78.3 66.9
North Korea 75.9 67.8
Haiti 68.7 63.3
Nigeria 63.3 59.5
Somalia 58.1 53.4

The numbers in Table tbl-life-expectancy faithfully reflect the overall situation in the different countries. Yet, without adjustment, they are not well suited to inform about specific situations. For example, life expectancies are usually calculated separately for males and females, acknowledging a significant association of life expectancy with sex, not just the availability of medical care. We will call such a strategy “groupwise adjustment” because it’s based on acknowledging difference between groups. You’ll see similar groupwise adjustment of life expectancy on the basis of race/ethnicity.

Over many years teaching epidemiology at Macalester College, I asked students to consider life-expectancy tables and make policy suggestions for improving things. Almost always, their primary recommendations involved improving access to health care, especially for the elderly.

But life expectancy is not mainly, or even mostly, about old age. Two critical determinants are infant mortality and lethal activities by males in their late teenage and early adult years. If we want to look at conditions in the elderly, we need to consider elderly people separately, not mixed in with infants, children, and adolescents. For reasons we won’t explain here, with life expectancy calculations it’s routine to calculate a separate “life expectancy at age X” for each age year. Table tbl-life-expectancy-at-70 shows, according to the World Health Organization, how many years longer a 70-year old can expect to live. The 30-year difference between Japan and Somalia seen in Table tbl-life-expectancy is reduced, for 70-year olds, to about a decade. The differences between males and females are similarly reduced

Table 12.2: Life expectancy at age 70. (Main source: World Health Organization) average of 65-74 year olds)
Country Female Male
Japan 21.3 17.9
Canada 18.0 15.6
Spain 17.0 14.0
United States 18.3 16.3
Russia 16.2 12.2
Bolivia 13.6 13.0
Haiti 12.9 12.1
Somalia 11.6 9.7

Adjustment with per

The previous example demonstrated adjustment by comparing similar subgroups. Here, we focus on adjustment by converting quantities into rates . For instance, “10 miles” is a quantity of distance. But “10 miles per hour” is a rate that compares the distance travelled to the time taken for the trip. Rates are always quotients, one quantity divided by another.

Often, the denominator of a rate—recall that quotients consist of a “numerator” divided by a “denominator”—is often a duration of time, but not always. Some examples:

  • “Dollars per gallon” for gasoline prices.
  • “Pounds per square inch” as in measuring air pressure.
  • “Euros per dollar” for expressing an exchange rate between two currencies.
  • “Children per woman” is a way of expressing fertility rates.
  • “Percent per year” is a common way of expressing a rate of growth, as with interest accumulating on a student loan.

In everyday speech, the word per is used to identify the quantity as a rate and serves grammatically to separate the numerator of the quotient from the denominator.

Rates are sometimes confusing to the unpracticed ear. For instance, some rates are constructed with two divisions. Physics students learn to express acceleration as “meters per second per second.” Similarly, a country’s birth rate can be expressed by “births per year per 1000 population.”

In economics and governance, rates often involve taking a total quantity and dividing it by the size of the population. For instance, total yearly spending on chewing gum in the US is estimated to be 2.4 billion dollars. The size of the population in the US is about 340 million people. Expressed as a rate, chewing-gum spending is about 7 dollars per person.

Very often, such “per person” rates are expressed using Latin: per capita.

“In 2020, children (0-18) accounted for 23 percent of the population and 10 percent of personal health care (PHC) spending, working age adults (19-64) accounted for 60 percent of the population and 53 percent of PHC, and older adults (65 and older) account for 17 percent of the population and 37 percent of PHC.”

Figure 12.1: Personal health-care spending as a fraction of the total population for different age groups. Source: US Centers for Medicare Studies
Table 12.3: A tabular arrangement of the data from the Centers for Medicare Studies
group age span population PHC spending
children 0-18 23% 10%
working age adults 19-64 60% 53%
older adults 65+ 17% 37%

The textual presentation of data in Figure fig-CMS-spending, presents relevant information but obscures the patterns. The author would have done better by placing the numbers that are to be compared to one another next to one another. A tabular organization makes it much easier to compare the relative population sizes of the age groups. For instance, the population column of Table tbl-PHC-spending shows at a glance that the population of children and older adults are about the same.

Similarly, the table’s “PHC spending” column makes it obvious that PHC spending is much higher for working age adults than for either children or older adults.

In comparing the spending between groups, it can be helpful to take into account the differing population sizes. A per capita adjustment—spending divided by population size—accomplishes it. For instance, the per capita adjustment for children is 10% / 23%, that is, 0.43. Table tbl-per-capita-spending shows the per capita spending for all three age groups.

Table 12.4: Adjusting spending for the size of the population gives a clearer indication of how spending compares between the different age groups.
group age population spending spending per capita
children 0-18 23% 10% 0.43
working age adults 19-64 60% 53% 0.88
older adults 65+ 17% 37% 2.18

Including the per capita adjusted spending in the table makes it easy to see an important pattern: older adults have much higher health spending (per person) than the other groups.

The method of adjustment by dividing one quantity by another has much broader applications. To illustrate, let’s return to the example of college grades from sec-grade-joins. There, we calculated using simple wrangling each student’s grade-point average and an instructor grade-giving average. The instructor’s grade-giving average varies so much that it seems short-sighted to neglect it as a factor in determining a student’s grade in that instructor’s courses.

An adjustment for the instructor can be made by constructing a per-type index. An instructor gave each grade, but instead of considering the grade literally, let’s divide the grade by the grade-giving average of the instructor involved.

We can consider the instructors’ iGPA to calculate an instructor-adjusted GPA for students. We create a data frame with the instructor ID and numerical grade point for every grade in the Grades and Sessions tables. First, we use “joins” to bring together the tables from the database.

Extended_grades <- Grades |> 
  left_join(Sessions) |>
  left_join(Gradepoint) |>
  select(sid, iid, sessionID, gradepoint)
sid iid sessionID gradepoint
S32418 inst268 session2911 3.00
S32328 inst436 session3524 3.66
S32250 inst268 session2911 2.66
S32049 inst436 session2044 3.33
S31914 inst436 session2044 3.66
S31905 inst436 session2044 4.00
S31833 inst436 session3524 3.33
S31461 inst264 session1904 4.00
S31197 inst436 session3524 3.00
S31194 inst264 session1904 2.00
      ... for 6,124 rows altogether
Figure 12.2: … for 364 instructors altogether

Next, calculate the instructor-by-instructor “grade-giving average” (gga):

Instructors <- Extended_grades |>
  summarize(gga = mean(gradepoint, na.rm = TRUE), .by = iid)
Show_these
iid gga
inst436 3.583778
inst264 2.973500
inst268 3.062195

Three rows from the Instructors data frame.

Joining the Instructors data frame with Extended_grades puts the grade earned and the average grade given next to one another. The unit of observation is still a student receiving a grade in a class session.

With_instructors <- 
  Extended_grades |>
  left_join(Instructors)
sid iid sessionID gradepoint gga
S32310 inst436 session2193 3.66 3.58
S31794 inst436 session2541 3.66 3.58
S32289 inst264 session2235 4.00 2.97
S31461 inst264 session1904 4.00 2.97
S32211 inst268 session2650 2.33 3.06
S32250 inst268 session2911 2.66 3.06
      ... for 6,124 rows altogether

Joining Extended_grades with Instructors.

Make the per adjustment by dividing gradepoint by gga to create a grade index. We will then average this index for each student to create each student’s instructor-adjusted GPA (adj_gpa), shown in Table tbl-adj-gpa.

Adjusted_gpa <-
  With_instructors |>
  mutate(index = gradepoint / gga) |>
  summarize(adj_gpa = mean(index, na.rm = TRUE), .by = sid)
sid adj_gpa
S31197 0.958
S31914 1.040
S31461 1.150
S32250 0.928
S31194 0.998
S32418 0.933
S32049 0.981
S32328 1.020
      ... for 443 students altogether.

Adjustment by modeling

unadjusted <- FARS |> model_train(crashes ~ year) |>
  model_eval(data = FARS)

adjusted <- FARS |> 
  model_train(crashes ~ year + vehicle_miles) |>
  model_eval(data = FARS |> mutate(vehicle_miles=3000))

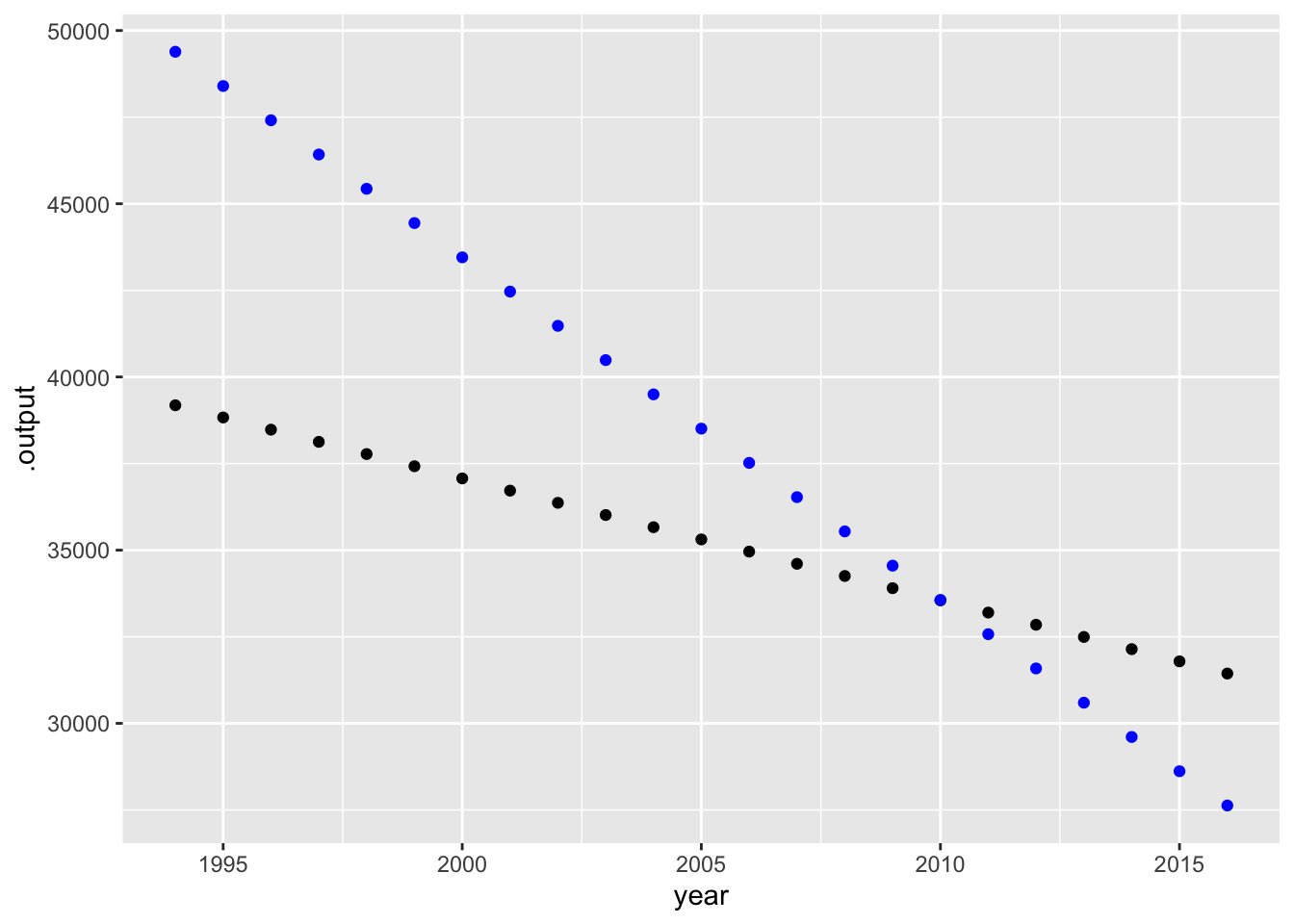
gf_point(.output ~ year, data = unadjusted) |>
  gf_point(.output ~ year, data = adjusted, color = "blue")

We will use the word “adjustment” to name the statistical techniques by which “other things” are considered. Those other things, as they appear in data, are called “covariates.”

“Per” adjusting for a covariate by creating an appropriate quotient is an important and somewhat intuitive technique. Less intuitive, but sometimes more powerful, is using a statistical model to accomplish the adjustment.

To illustrate, consider the data on auto traffic safety compiled by the US Department of Transportation. The data frame FARS (short for “Fatality Analysis Recording System”) records data from 1994 to 2016. Did driving become safer or more dangerous over that period?

We can look at the relationship between the number of crashes each year and the year itself, as in Figure fig-fars-by-year.

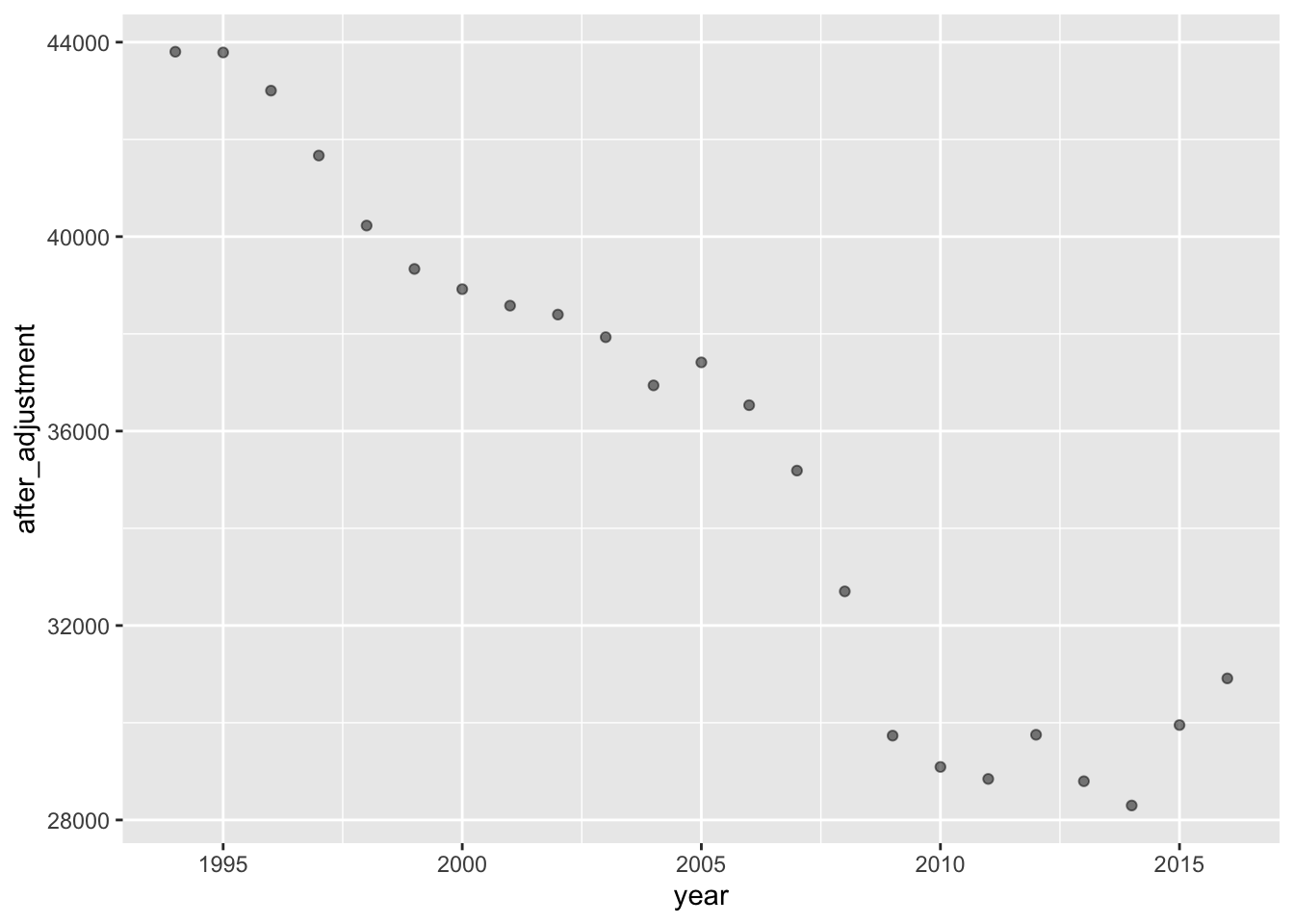
FARS |> mutate(rate = crashes / vehicle_miles) |>
  mutate(after_adjustment = rate * 2849) |>
  point_plot(after_adjustment ~ year)

FARS |> 
  point_plot(crashes ~ year, annot = "model")

Figure 12.3: The number of traffic crashes was more-or-less level up through 2006, then dropped off sharply until 2010. Perhaps the last two years show a return to the pre-2006 situation.

An important factor in the number of crashes in a year is the amount of driving in that year. FARS records this as vehicle_miles, as if all cars shared the same odometer. But the number of crashes might be influenced by the number of licensed drivers (more inexperienced drivers leading to more crashes?), or the number of registered vehicles (older cars still on the road leading to more crashes?). We can take all these into account by building a model and evaluating it for each year at specified values for each of the covariates. We’ll use the mean of each of the covariates for the model evaluation.

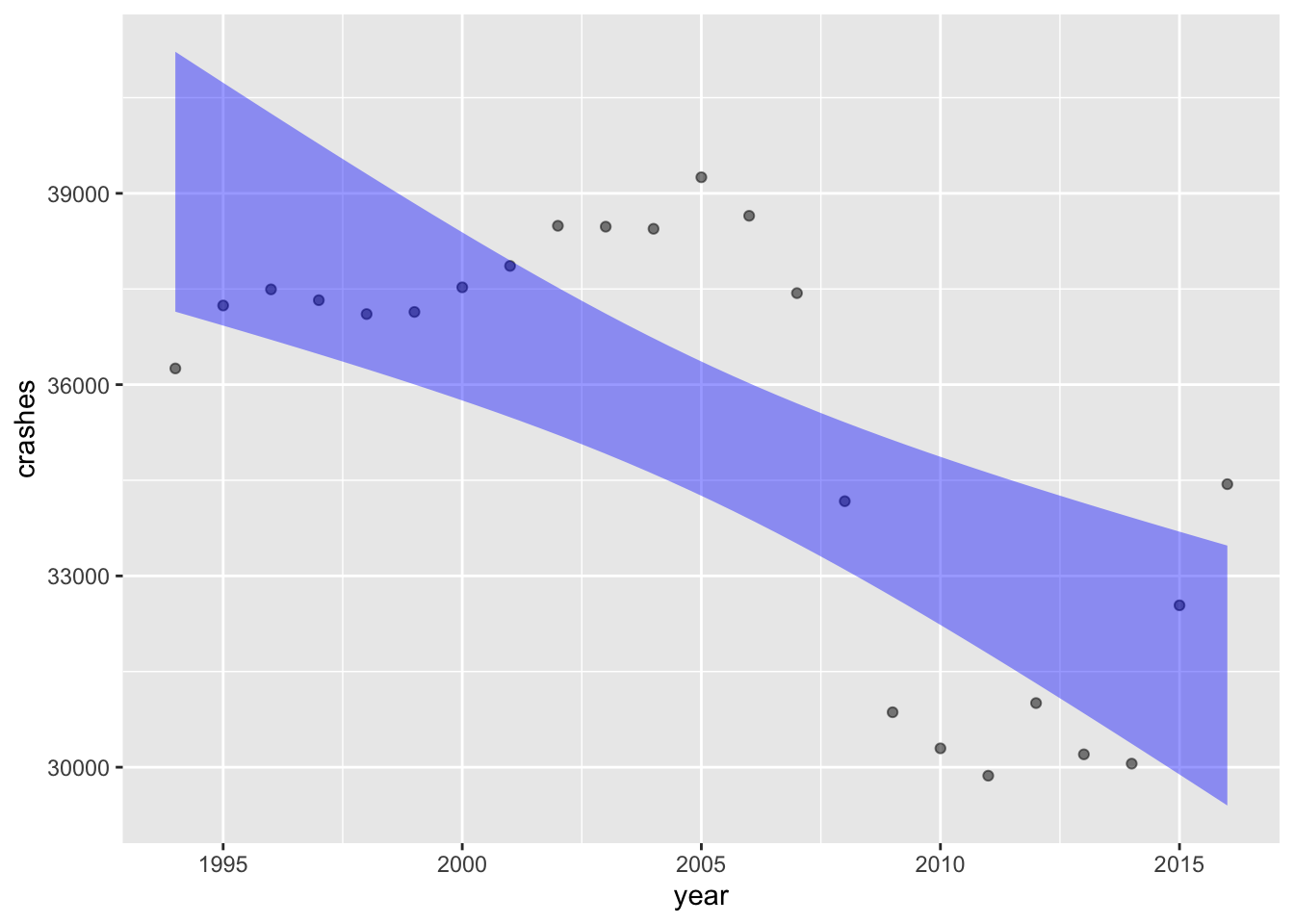
FARS |>
  summarize(miles = mean(vehicle_miles), 
            vehicles = mean(registered_vehicles), 
            drivers = mean(licensed_drivers))
miles vehicles drivers
2848.957 240101.2 199337.4

Now, to build the model:

Mod <- FARS |> 
  model_train(crashes ~ year + vehicle_miles +
                registered_vehicles + licensed_drivers)
Evaluate_at <- FARS |>
  mutate(vehicle_miles = 2849,
         registered_vehicles = 240101,
         licensed_drivers = 199337)
Mod |> model_eval(data = Evaluate_at) |> 
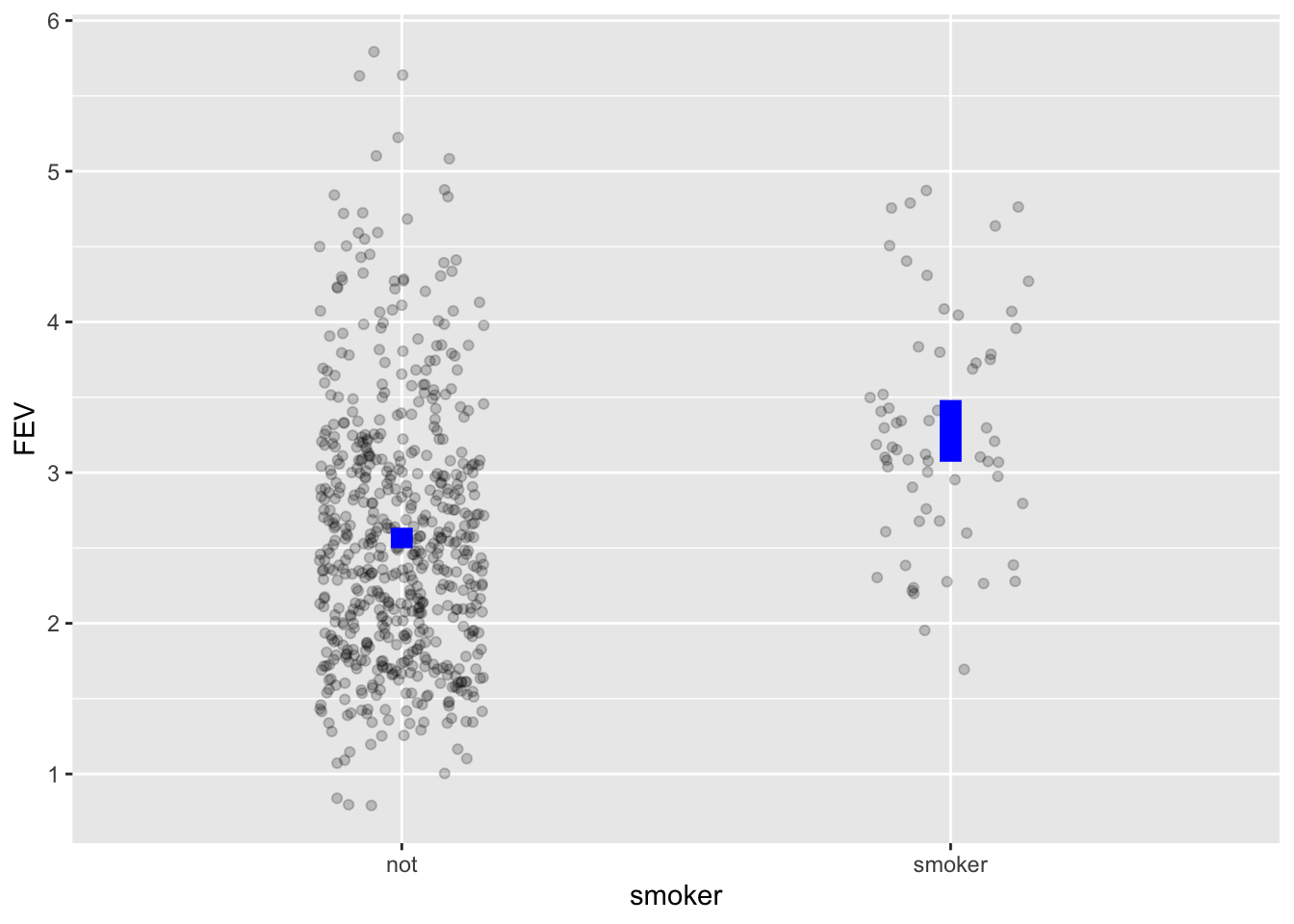
  point_plot(.output ~ year)

To illustrate, consider the Childhood Respiratory Disease Study which examined possible links between smoking and pulmonary capacity, as measured by “forced expiratory volume” (FEV). The data are recorded in the CRDS data frame. The unit of observation is a child. CRDS contains several variables including the “forced expiratory volume” (FEV variable) and smoker. Higher forced expiratory volume is a sign of better respiratory capacity. Knowing what we do today about the dangers of smoking, we might hypothesize that the FEV measurement will be related to smoking.

# IN DRAFT: Replace CRDS with FEV until the LSTbook package is updated.
CRDS |> 
  point_plot(FEV ~ smoker, annot = "model",
             point_ink = 0.2, model_ink = 1)

Figure 12.4: Forced expiratory volume as a function of smoking status. A typical non-smoker has an FEV of about 2.5, while typical non-smokers have a higher FEV: about 3.25.

To judge from Figure fig-fev-smoking, children who smoke tend to have larger FEV than their non-smoking peers. This counter-intuitive result might give pause. Is there some covariate that would clarify the picture?

Since FEV largely reflects the physical capacity of the lungs, perhaps we need to consider the child’s age or height. “consider age or height” we mean “adjust for age or height.”

There are two phases for modelling-based adjustment, one requiring careful thought and understanding of the specific system under study, the other—the topic of this section—involving only routine, straightforward modeling calculations.

Here’s the calculation of the model .output as a function of smoker, without any adjustment. That is, smoker is the only explanatory variable.

Table 12.5: The unadjusted model values, that is, the model output from FEV ~ smoker without any covariates. 
CRDS |>
  model_train(FEV ~ smoker) |>
  model_eval(data = CRDS) |>
  select(.output, smoker) |>
  unique()
.output smoker
2.566143 not
3.276861 smoker

The adjusted model involves three phases:

Phase 1: Choose relevant covariates for adjustment. This almost always involves familiarity with the real-world context. Here, we’ll use height and age, reflecting the fact that bigger kids tend to have larger FEV.

Phase 2: Build a model with the covariates from Phase 1 as explanatory variables.

adjusted_model <-
  CRDS |>
  model_train(FEV ~ smoker + height + age)

Phase 3: Evaluate the adjusted model but don’t use the actual values of the covariates. Instead, standardize the values of the covariates to constant, representative values. We’ll use age 15 and height 60 inches.

::: {#tbl-with-adjustment}

adjusted_model |>
  model_eval(
    data = CRDS |> mutate(age = 15, height = 60)
  ) |>
  select(.output, smoker) |>
  unique()
.output smoker
2.825793 not
2.715561 smoker

Models highlight trends in the data, but the trends in this case are different with and without adjustment. Adjustment for age and height raises the model output for non-smokers and lowers it for smokers.

This is the core of adjustment: comparing individual specimens after putting them on the same footing, that is, ceteris paribus.

Exercises

Exercise 12.1  

Consider again the FARS data on the number of crashes each year. The raw data are plotted in Figure fig-fars-by-year. (Hover over the link to see the graph.) But presumably, the total number of crashes is related to the “amount of driving” in that year.

A. Here’s a graph of accidents per vehicle mile over the years.

FARS |>
  mutate(rate = crashes / vehicle_miles) |>
  point_plot(rate ~ year)

How does the year-to-year pattern of the accident rate compare to the year-to-year pattern of the raw number of accidents?

B. There are several other ways to measure “the amount of driving.” Following the per-capita style, we might want to create an crash rate that is number of crashes divided by the size of the population. Or maybe divide by the number of licenced_drivers or the number of registered_vehicles.

Create each of these rates and plot them versus year. Comment on whether they show the same pattern as in (A).

Comment: Vehicle-miles driven can change quickly from one year to the next, for example in response to the “Great Recession” of 2008. But population or the number of licensed drivers or registered vehicles can change only slowly.

id=Q12-101

Exercise 12.2  

Age adjustment in Whickham.

id=Q12-102

Exercise 12.3  

Knives and forks example from p. 147 in Milo’s book.

id=Q12-103

Exercise 12.4  

Participation-adjusted school performance. Something is not working here. You’ll need to take spending into account

SAT |> model_train(sat ~ frac + expend) |> conf_interval()
term .lwr .coef .upr
(Intercept) 949.908859 993.831659 1037.754459
frac -3.283679 -2.850929 -2.418179
expend 3.788291 12.286518 20.784746 
SAT |> select(state, sat, frac, expend) |>
  mutate(adj_sat = sat - 0.00297*(50-frac) + 0.0127*(6 - expend))
state sat frac expend adj_sat
Alabama 1029 8 4.405 1028.8955
Alaska 934 47 8.963 933.9535
Arizona 944 27 4.778 943.9472
Arkansas 1005 6 4.459 1004.8889
California 902 45 4.992 901.9980
Colorado 980 29 5.443 979.9447
Connecticut 908 81 8.817 908.0563
Delaware 897 68 7.030 897.0404
Florida 889 48 5.718 888.9976
Georgia 854 65 5.193 854.0548
Hawaii 889 57 6.078 889.0198
Idaho 979 15 4.210 978.9188
Illinois 1048 13 6.136 1047.8884
Indiana 882 58 5.826 882.0260
Iowa 1099 5 5.483 1098.8729
Kansas 1060 9 5.817 1059.8806
Kentucky 999 11 5.217 998.8941
Louisiana 1021 9 4.761 1020.8940
Maine 896 68 6.428 896.0480
Maryland 909 64 7.245 909.0258
Massachusetts 907 80 7.287 907.0728
Michigan 1033 11 6.994 1032.8715
Minnesota 1085 9 6.000 1084.8782
Mississippi 1036 4 4.080 1035.8878
Missouri 1045 9 5.383 1044.8861
Montana 1009 21 5.692 1008.9178
Nebraska 1050 9 5.935 1049.8791
Nevada 917 30 5.160 916.9513
New Hampshire 935 70 5.859 935.0612
New Jersey 898 70 9.774 898.0115
New Mexico 1015 11 4.586 1014.9021
New York 892 74 9.623 892.0253
North Carolina 865 60 5.077 865.0414
North Dakota 1107 5 4.775 1106.8819
Ohio 975 23 6.162 974.9178
Oklahoma 1027 9 4.845 1026.8929
Oregon 947 51 6.436 946.9974
Pennsylvania 880 70 7.109 880.0453
Rhode Island 888 70 7.469 888.0407
South Carolina 844 58 4.797 844.0390
South Dakota 1068 5 4.775 1067.8819
Tennessee 1040 12 4.388 1039.9076
Texas 893 47 5.222 893.0010
Utah 1076 4 3.656 1075.8931
Vermont 901 68 6.750 901.0439
Virginia 896 65 5.327 896.0531
Washington 937 48 5.906 936.9953
West Virginia 932 17 6.107 931.9006
Wisconsin 1073 9 6.930 1072.8664
Wyoming 1001 10 6.160 1000.8792

Examples of adjustment using the method described at the end of the last section.

id=Q12-104

Exercise 12.5  

Adjustment for length in KidsFeet.

id=Q12-105

Exercise 12.6  

MAKE AN EASY EXERCISE OUT OF THIS. NOTE THAT THE PRESENTATION OF THE AGE DISTRIBUTION IS MUCH LIKE A VIOLIN PLot.

Maybe ask what’s happening at the top of the pyramid: Is the sharp decline in population owing to death rates, or is it the passage of the teenage hump from 1972 through 50 years of aging.

The World Health Organization standard population

There is much to be learned by comparing health statistics in different countries. For example, in comparing countries with the same level of income, etc., the country with the best health statistics might have useful examples for public policy. Of course, meaningful health statistics should be adjusted for age. Adjustment is done by reference to a “standard population.” Figure fig-who-standard-population shows the World Health Organizations standard population. Following the pattern observed in most of the world, younger people predominate. A similar pattern was seen in the US many decades ago, but the US population has changed dramatically and now includes roughly equal numbers of people over a wide span of ages. Even so, the WHO standard population is valuable for comparing US health statistics to those in other countries that have a different age distribution.

NEED TO FIX THE FOLLOWING CHUNK

Comparing the World Health Organization’s standard population to the US population in 1972 and 2021. Females are shown in blue, males in green.

Figure 12.5

id=Q12-201

Exercise 12.7  

See rural vs. urban mortality rates at https://jamanetwork.com/journals/jama/fullarticle/2780628

From Google: According to a 2021 National Center for Health Statistics (NCHS) data brief, Trends in Death Rates in Urban and Rural Areas: United States, 1999–2019, the age-adjusted death rate in rural areas was 7% higher than that of urban areas, and by 2019 rural areas had a 20% higher death rate than urban areas. https://www.ruralhealthinfo.org/topics/rural-health-disparities#:~:text=According%20to%20a%202021%20National,death%20rate%20than%20urban%20areas.

Adjusting for age

“Life tables” are compiled by governments from death certificates.

LTraw <- readr::read_csv("www/life-table-raw.csv")
Rows: 120 Columns: 7
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (7): age, male, mnum, mlife_exp, female, fnum, flife_exp

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
head(LTraw)
age male mnum mlife_exp female fnum flife_exp
0 0.005837 100000 74.12 0.004907 100000 79.78
1 0.000410 99416 73.55 0.000316 99509 79.17
2 0.000254 99376 72.58 0.000196 99478 78.19
3 0.000207 99350 71.60 0.000160 99458 77.21
4 0.000167 99330 70.62 0.000129 99442 76.22
5 0.000141 99313 69.63 0.000109 99430 75.23

Wrangling to a more convenient format (for our purposes):

LT <- tidyr::pivot_longer(LTraw |> select(age, male, female), c("male", "female"), names_to="sex", values_to="mortality")
LT
age sex mortality
0 male 0.005837
0 female 0.004907
1 male 0.000410
1 female 0.000316
2 male 0.000254
2 female 0.000196
3 male 0.000207
3 female 0.000160
4 male 0.000167
4 female 0.000129
5 male 0.000141
5 female 0.000109
6 male 0.000123
6 female 0.000100
7 male 0.000113
7 female 0.000096
8 male 0.000108
8 female 0.000092
9 male 0.000114
9 female 0.000089
10 male 0.000127
10 female 0.000092
11 male 0.000146
11 female 0.000104
12 male 0.000174
12 female 0.000123
13 male 0.000228
13 female 0.000145
14 male 0.000312
14 female 0.000173
15 male 0.000435
15 female 0.000210
16 male 0.000604
16 female 0.000257
17 male 0.000814
17 female 0.000314
18 male 0.001051
18 female 0.000384
19 male 0.001250
19 female 0.000440
20 male 0.001398
20 female 0.000485
21 male 0.001524
21 female 0.000533
22 male 0.001612
22 female 0.000574
23 male 0.001682
23 female 0.000617
24 male 0.001747
24 female 0.000655
25 male 0.001812
25 female 0.000700
26 male 0.001884
26 female 0.000743
27 male 0.001974
27 female 0.000796
28 male 0.002070
28 female 0.000851
29 male 0.002172
29 female 0.000914
30 male 0.002275
30 female 0.000976
31 male 0.002368
31 female 0.001041
32 male 0.002441
32 female 0.001118
33 male 0.002517
33 female 0.001186
34 male 0.002590
34 female 0.001241
35 male 0.002673
35 female 0.001306
36 male 0.002791
36 female 0.001386
37 male 0.002923
37 female 0.001472
38 male 0.003054
38 female 0.001549
39 male 0.003207
39 female 0.001637
40 male 0.003333
40 female 0.001735
41 male 0.003464
41 female 0.001850
42 male 0.003587
42 female 0.001950
43 male 0.003735
43 female 0.002072
44 male 0.003911
44 female 0.002217
45 male 0.004137
45 female 0.002383
46 male 0.004452
46 female 0.002573
47 male 0.004823
47 female 0.002777
48 male 0.005214
48 female 0.002984
49 male 0.005594
49 female 0.003210
50 male 0.005998
50 female 0.003476
51 male 0.006500
51 female 0.003793
52 male 0.007081
52 female 0.004136
53 male 0.007711
53 female 0.004495
54 male 0.008394
54 female 0.004870
55 male 0.009109
55 female 0.005261
56 male 0.009881
56 female 0.005714
57 male 0.010687
57 female 0.006227
58 male 0.011566
58 female 0.006752
59 male 0.012497
59 female 0.007327
60 male 0.013485
60 female 0.007926
61 male 0.014595
61 female 0.008544
62 male 0.015702
62 female 0.009173
63 male 0.016836
63 female 0.009841
64 male 0.017908
64 female 0.010529
65 male 0.018943
65 female 0.011265
66 male 0.020103
66 female 0.012069
67 male 0.021345
67 female 0.012988
68 male 0.022750
68 female 0.014032
69 male 0.024325
69 female 0.015217
70 male 0.026137
70 female 0.016634
71 male 0.028125
71 female 0.018294
72 male 0.030438
72 female 0.020175
73 male 0.033249
73 female 0.022321
74 male 0.036975
74 female 0.025030
75 male 0.040633
75 female 0.027715
76 male 0.044710
76 female 0.030631
77 male 0.049152
77 female 0.033900
78 male 0.054265
78 female 0.037831
79 male 0.059658
79 female 0.042249
80 male 0.065568
80 female 0.047148
81 male 0.072130
81 female 0.052545
82 male 0.079691
82 female 0.058685
83 male 0.088578
83 female 0.065807
84 male 0.098388
84 female 0.074052
85 male 0.109139
85 female 0.083403
86 male 0.120765
86 female 0.093798
87 male 0.133763
87 female 0.104958
88 male 0.148370
88 female 0.117435
89 male 0.164535
89 female 0.131540
90 male 0.182632
90 female 0.146985
91 male 0.202773
91 female 0.163592
92 male 0.223707
92 female 0.181562
93 male 0.245124
93 female 0.200724
94 male 0.266933
94 female 0.219958
95 male 0.288602
95 female 0.239460
96 male 0.309781
96 female 0.258975
97 male 0.330099
97 female 0.278225
98 male 0.349177
98 female 0.296912
99 male 0.366635
99 female 0.314727
100 male 0.384967
100 female 0.333610
101 male 0.404215
101 female 0.353627
102 male 0.424426
102 female 0.374844
103 male 0.445648
103 female 0.397335
104 male 0.467930
104 female 0.421175
105 male 0.491326
105 female 0.446446
106 male 0.515893
106 female 0.473232
107 male 0.541687
107 female 0.501626
108 male 0.568772
108 female 0.531724
109 male 0.597210
109 female 0.563627
110 male 0.627071
110 female 0.597445
111 male 0.658424
111 female 0.633292
112 male 0.691346
112 female 0.671289
113 male 0.725913
113 female 0.711567
114 male 0.762209
114 female 0.754261
115 male 0.800319
115 female 0.799516
116 male 0.840335
116 female 0.840335
117 male 0.882352
117 female 0.882352
118 male 0.926469
118 female 0.926469
119 male 0.972793
119 female 0.972793

Questions:

  • When were people aged 35-39 in 1972 born? Why are there so few of them?
  • How old would you have to be in 1972 to be part of the “baby boom?” Can you see the echo of the baby boom in 2021?
  • How many 85+ year-olds will there be in 2040?

The raw data:

Code 
Pop2020 <- readr::read_csv("www/nc-est2021-agesex-res.csv",
                           show_col_types=FALSE) |>
  filter(SEX > 0, AGE<999) |>
  mutate(sex = ifelse(SEX==1, "female", "male"), 
         age=AGE, pop=ESTIMATESBASE2020) |> 
  select(age, sex, pop)
Pop2020 |> tail()
age sex pop
95 male 132299
96 male 105435
97 male 79773
98 male 57655
99 male 43072
100 male 78474

US mortality at actual age distribution involves joining the data from these two data frames.

Overall <- Pop2020 |> left_join(LT)
Joining with `by = join_by(age, sex)`
head(Overall)
age sex pop mortality
0 female 1907982 0.004907
1 female 1928926 0.000316
2 female 1980392 0.000196
3 female 2028781 0.000160
4 female 2068682 0.000129
5 female 2081588 0.000109

The calculation is simple wrangling:

Overall |> 
  summarize(mortality = 100000*sum(pop*mortality)/sum(pop),
  .by = sex)
sex mortality
female 708.1769
male 1351.4683

US mortality at WHO standard age distribution:

Standard <- tibble(
  age = 0:99,
  pop = popfun(age)
)
Overall <- Standard |> left_join(LT)
Overall |> 
  summarize(mortality = 100000*sum(pop*mortality)/sum(pop), 
  .by = sex)

Age-adjusted death rates over time

From the SSA (p. 15)

id=Q12-301

Enrichment topics

To illustrate, we return to the college grades example in sec-per-adjustment. There, we did a per adjustment of each grade by the average of all the grades assigned by the instructor (the “grade-giving average”: gga).

Now we want to examine how to incorporate other factors into the adjustment, for instance class size (enroll) and class level. We will also change from the politically unpalatable instructor-based grade-given average to using department (dept) as a covariate.

To start, we point out that the conventional GPA can also be found by modeling gradepoint ~ sid.

Joined_data <-   Grades |> 
  left_join(Sessions) |>
  left_join(Gradepoint) 
Raw_model <- 
  Joined_data |> 
  model_train(gradepoint ~ sid)

The model values from Raw_model will be the unadjusted (raw) GPA. We can compute those model values by making a data frame with all the input values for which we want an output:

Students <- Grades |> select(sid) |> unique()

Now evaluate Raw_model for each of the inputs in Students to find the model value (called .output by model_eval()).

Raw_gpa <- Raw_model |>
  model_eval(Students) |>
  select(sid, raw_gpa = .output)

The advantage of such a modeling approach is that we can add covariates to the model specification in order to adjust for them. To illustrate, we will adjust using enroll, level, and dept:

Adjustment_model <-
  Joined_data |>
  model_train(gradepoint ~ sid + enroll + level + dept)

As we did before with Raw_model, we will evaluate Adjustment_model at all values of sid. But we will also hold constant the enrollment, level, and department by setting their values. For instance, Table tbl-gpa-model-adjusted shows every student’s GPA as if their classes were all in department D, at the 200 level, and with an enrollment of 20.

Table 12.6 
Inputs <- Students |>
  mutate(dept = "D", level = 200, enroll = 20)
Model_adjusted_gpa <-
  Adjustment_model |>
  model_eval(Inputs) |>
  rename(modeled_gpa = .output)

In sec-adjustment-by-modeling, we calculated three different versions of the GPA:

  1. The raw GPA, which we calculated in two equivalent ways, with summarize(mean(gradepoint), .by = sid) and with the model gradepoint ~ sid.
  2. The grade-given average used to create an index that involves gradepoint / gga.
  3. The model using covariates level, enroll, and dept.

The statistical thinker knows that GPA is a social construction, not a hard-and-fast reality. Let’s see to what extent the different versions agree.

MAKE THIS REFER TO THE instructor-adjusted GPA in Lesson 12. Maybe use it to introduce rank.

Does adjusting the grades in this way make a difference? We can compare the index to the raw GPA, calculated in the conventional way.

ABOUT COMPARING THE THREE DIFFERENT FORMS OF ADJUSTMENT.

The data file containing the three forms of adjusted GPA is in ../../LSTtext/www/Three-gpas.rda”

Introduce sensitivity, the idea that the result should not depend strongly on details which we don’t think should be critical. Then introduce variance of the residuals from comparing each pair.

# Convert to work with `Three_gpas`
Raw_gpa |>
  left_join(Adjusted_gpa) |>
  left_join(Model_adjusted_gpa) |>
  mutate(raw_vs_adj = rank(raw_gpa) - rank(grade_index),
         raw_vs_modeled = rank(raw_gpa) - rank(modeled_gpa),
         adj_vs_modeled = rank(grade_index) - rank(modeled_gpa)) |>
  select(contains("_vs_")) |> 
  pivot_longer(cols = contains("_vs_"), names_to = "comparison",
               values_to = "change_in_rank") |>
  summarize(var(change_in_rank), .by = comparison) |>
  kable()

This is, admittedly, a lot of wrangling. The result is that the two methods of adjustment agree with one another—a smaller variance of the change in rank—much more than the raw GPA agrees with either. This suggests that the adjustment is identifying a genuine pattern rather than merely randomly shifting things around.