Chapter 12 Confidence in Models

To know one’s ignorance is the best part of knowledge. – Lao-Tsu (6th century BC), Chinese philosopher

Doubt is not a pleasant condition, but certainty is an absurd one. – Voltaire (1694-1778), French writer and philosopher

If you are a skilled modeler, you try to arrange things so that your model coefficients are random numbers.

That statement may sound silly, but before you jump to conclusions it’s important to understand where the randomness comes from and why it’s a good thing. Then you can use the tools in the previous two chapters to deal with the randomness and interpret it.

Recall the steps in building a statistical model:

Collect data. This is the hardest part, often involving great effort and expense.
Design your model, choosing the response variable, the explanatory variables, and the model terms. (It’s sensible to have the design in mind before you collect your data, so you know what data are needed.)
Fit the model design to your data.

Step (3) is entirely deterministic. Given the model design and the data to which the model is to be fitted, fitting is an automatic process that will give the same results every time and on every computer. There is no randomness there. (There is some choice in choosing which to remove from a set of vectors containing redundancy, but that is a choice, not randomness. In any event, the fitted model values are not affected by this choice.)

Step (2) appears, at first glance, to leave space for chance. After all, when explanatory terms are collinear, as they often are, the fitted coefficients on any term can depend strongly on which other terms have been included in the model. The coefficients depend on the modeler’s choices. But this means only that the coefficients reflect the beliefs of the modeler. If those beliefs aren’t random, then the randomness of coefficients doesn’t stem from the modeler.

It’s step (1) that introduces the randomness. In collecting data, the sample cases are selected from a population. As described in Chapter 2, it’s advantageous to make a random selection from the population; this helps to make the sample representative of the population.

Saying something is random means that it is uncertain, that if the process were repeated again the result might be different. When a sample is selected at random, the particular sample that is produced is just one of a set of possibilities. One can imagine other possibilities that might have come about from the luck of the draw.

Insofar as the sample is random, the coefficients that come from fitting the model design to the sample are also random. The randomness of model coefficients means that the coefficients that come from a model design fitted to any particular data set are not likely to be an exact match to what you would get if the model design were fitted to the entire population. After all, the randomly selected sample is unlikely to be an exact match to the entire population.

It’s helpful to know how close the results from the sample are to what would have been obtained if the sample had been the entire population. Ultimately, the only way to know this for sure is to create a sample that is the entire population. Usually this is impractical and often it is impossible.

As described in Chapter 5, there is an approach that will give insight, even if it does not give certainty. To start, imagine that the sample were actually a census: a sample that contains the entire population. Repeating the study with a new sample would give exactly the same result because the new sample would be the same as the old one; it’s the same population.

When the sample is not the entire population, repeating the study won’t give the same result every time because the sample will include different members of the population. If the results vary wildly from one repeat to another, you have reason to think that the results are not a reliable indication of the population. If the results vary only a small amount from one repeat to another, then there’s reason to think that you have closely approximated the results that you would have gotten if the sample had been the entire population. The repeatability of the process indicates how well the modeler knows the coefficients, or, in a word, the precision of the coefficients.

Knowing the precision of coefficients is key in drawing conclusions from them. Consider Galton’s problem in studying whether height is a heritable trait. Had Galton known about modeling, he might have constructed a model like height ~ 1 + mother + father + sex. A relationship between the mother’s height and her child’s height should show up in the coefficient on mother. If there is a relationship, that coefficient should be non-zero.

Fitting the model to Galton’s data, the coefficient is 0.32. Is this non-zero? Yes, for this particular set of data. But how might it have been different if Galton repeated his sampling, selecting a new set of cases from the population? How precise is the coefficient? Until this is known, it’s mere bravado to say that a result of 0.32 means anything.

This chapter introduces methods that can be used to estimate the precision of coefficients from data. A standard format for presenting this estimation is the confidence interval. For instance, from Galton’s data, the estimated coefficient on mother is 0.32 ± 0.06, giving confidence that a different sample would also show a non-zero coefficient.

It’s important to contrast precision with accuracy. Precision is about repeatability. Accuracy is about how the result matches the real world. Ultimately, accuracy is what the modeler wants. A major reason to introduce modeling techniques beyond the simple group-wise models of Chapter 4 is to enable you to account for the multiple factors that shape outcomes. But the results of a model always depend on the choices the modeler makes, e.g., which explanatory variables to include, how to choose a sample, etc. The results can be accurate only if the modeler makes good choices. Knowing whether this is the case depends on knowing how the world really works, and this is what you are seeking to find out in the first place. Accuracy is elusive knowledge. Precision will have to suffice.

12.1 The Sampling Distribution & Model Coefficients

The same principles of sampling and re-sampling distributions introduced in Chapter 5 can be used to find confidence intervals on model coefficients.

To illustrate, consider the TenMileRace dataset (in the mosaicData package). This is a census containing the running times for all 8636 registered participants in the Cherry Blossom Ten Mile race held in Washington, D.C. in April 2005.

The variable net records the start-line to finish-line time of each runner. There are also variables age and sex. Any model would do to illustrate the sampling distribution. Try net ~ 1 + age + sex.

Just for reference, here are the coefficients when the model is fit to the entire population:

  Intercept   age   sexM
1      5339 16.89 -726.6

The coefficients indicate that runners who are one year older tend to take about 17 seconds longer to run the 10 miles.

Of course, if you knew the coefficients that fit the whole population, you would hardly need to collect a sample! But the purpose here is to demonstrate the effects of a random sampling process. The table below gives the coefficients from several sampling draws; each sample has n=100 cases randomly selected from the population. That is, each sample simulates the situation where someone has randomly selected n=100 cases.

  Intercept    age    sexM
1      5060 26.160  -731.2
2      5409 12.850  -930.5
3      5434 12.320  -463.7
4      5015 27.980 -1062.0
5      5505  9.837  -474.0
6      5485 13.600  -584.6
7      5187 17.240  -627.2
8      4783 31.940  -780.0

Judging from these few samples, there is a lot of variability in the coefficients. For example, the age coefficient ranges from 2.1 to 33.7 in just these few samples. Figure 12.1 shows the distribution of coefficients for the age and sex coefficients for the first eight out of 1000 repeats of the sampling process. Each of the samples has 100 cases randomly selected from the population. These distributions, which reflect the randomness of the sampling process, are called sampling distributions . It’s very common for sampling distributions to be bell-shaped and to be centered on the population value.

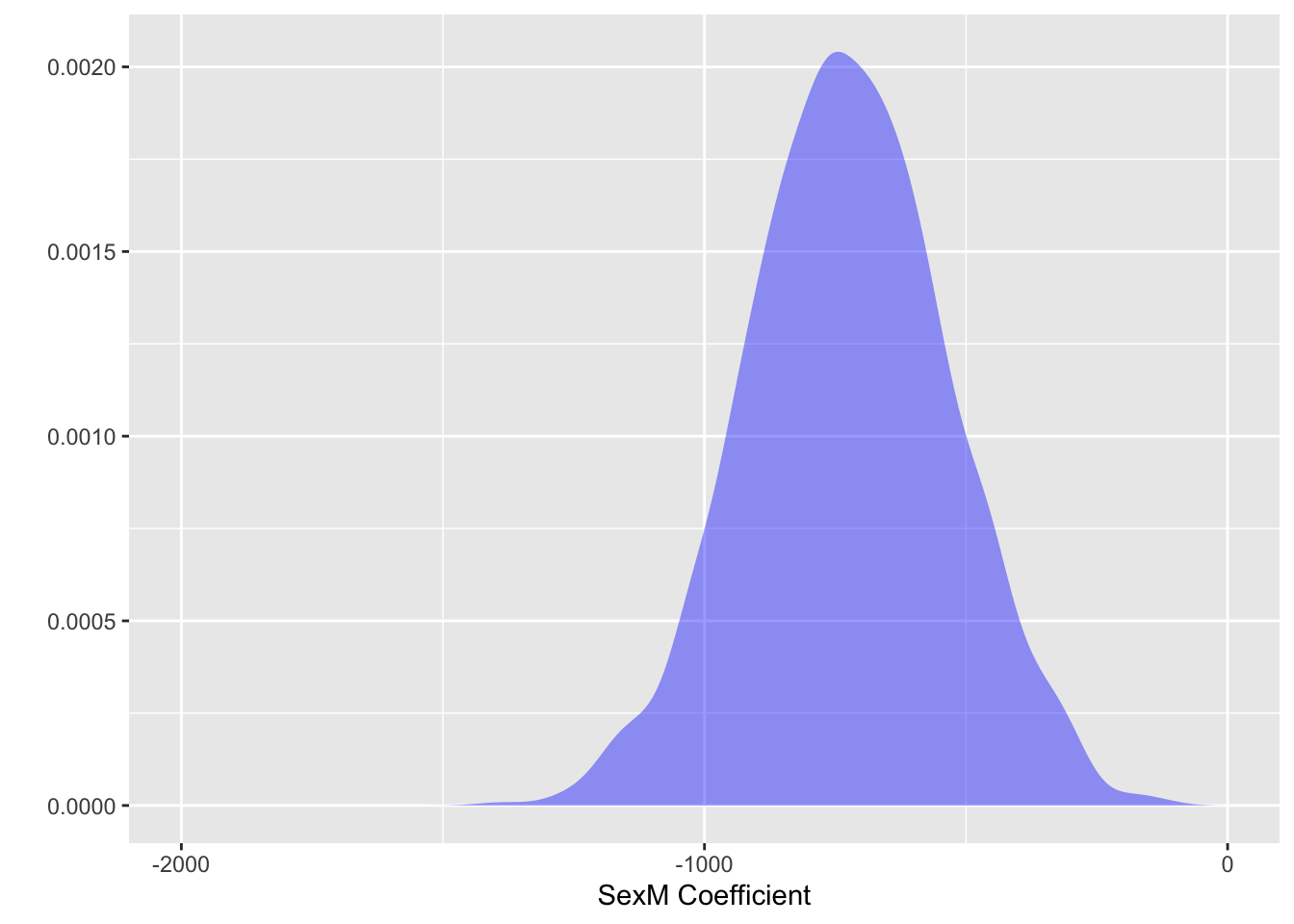
Sampling distributions for the `age` and `sex` coefficients for a sample size of n = 100. The bell-shaped distributions are centered on the population value.

Figure 12.1: Sampling distributions for the age and sex coefficients for a sample size of n = 100. The bell-shaped distributions are centered on the population value.

The width of the sampling distribution shows the reliability or repeatability of the coefficients. There are two common ways to summarize the width: the standard deviation and the 95% coverage interval.

An important item to add to your vocabulary is the “standard error.”

Sampling distributions, like other distributions, have standard deviations. The term standard error is used to refer to the standard deviation of a sampling distribution.

For the age coefficient, the standard error is about 9.5 seconds per year (keeping in mind the units of the data), and the standard error in sexM is about 192 seconds. These standard errors were calculated by drawing 10,000 repeats of samples of size n = 100, and fitting the model to each of the 10000 samples. This is easy to do on the computer, but practically impossible in actual field work.

Every model coefficient has its own standard error which indicates the precision of the coefficient. The size of the standard error depends on several things:

The quality of the data. The precision with which individual measurements of variables is made, or errors in those measurements, translates through to the standard errors on the model coefficients.
The quality of the model. The size of standard errors is proportional to the size of the residuals, so a model that produces small residuals tends to have small standard errors. However, collinearity or multi-collinearity among the explanatory variables tends to inflate standard errors.
The sample size n. Standard errors tend to get tighter the more data is used to fit the model. A simple relationship holds very widely; it’s worth remembering this rule:

The standard error typically gets smaller as the sample size n increases, but slowly; it’s proportional to 1/√n. This means, for instance, that to make the standard error 10 times smaller, you need a dataset that is 100 times larger.

12.2 Standard Errors and the Regression Report

Finding the standard error of a model coefficient would be straightforward if one could follow the procedure above: repeatedly draw new samples from the population, fit the model to each new sample, and collect the resulting coefficients from each sample to produce the sampling distribution. This process is impractical, however, because of the expense of collecting new samples.

Fortunately, there can be enough information in the original sample to make a reasonable guess about the sampling distribution. How to make this guess is the subject of Section 5.4. For now, it suffices to say that the guess is based on an approximation to the sampling distribution called the resampling distribution .

A conventional report from software, often called a regression report, provides an estimate of the standard error. Here is the regression report from the model net ~ 1 + age + sex fitted to a sample of size n = 50 from the running data:

            Estimate Std..Error t.value  p.value
(Intercept)   5250.0     34.800   151.0 p<0.0001
age             19.9      0.937    21.3 p<0.0001
sexM          -744.0     20.100   -37.1 p<0.0001

The coefficient itself is in the column labelled “Estimate.” The next column, labelled “Std. Error,” gives the standard error of each coefficient. You can ignore the last two columns of the regression report for now. They present the information from the first two columns in a different format.

12.3 Confidence Intervals

The regression report gives the standard error explicitly, but it’s common in many fields to report the precision of a coefficient in another way, as a confidence interval. This was introduced in Chapter 5 in the context of group-wise models, but it applies to other sorts of models as well.

A confidence interval is a little report about a coefficient like this one about the age coefficient in the regression table above: “29 ± 18 with 95% confidence.” The confidence interval involves three components:

Point Estimate The center of the confidence interval: 29 here. Read this directly from the regression report.
Margin of Error The half-width of the confidence interval: 18 here. This is two times the standard error from the regression report.
Confidence Level The percentage of the coverage interval. This is typically 95%. Since people get tired of saying the same thing over and over again, they often omit the “with 95% confidence” part of the report. This can be dangerous, since sometimes people use confidence levels other than 95%.

The purpose of multiplying the standard error by two is to make the confidence interval approximate a 95% coverage interval of the resampling distribution.

Example: Wage discrimination in trucking?

Section 10.4 looked at data from a trucking company to see how earnings differ between men and women. It’s time to revisit that example, using confidence intervals to get an idea of whether the data clearly point to the existence of a wage difference.

The model earnings ~ sex ascribed all differences between men and women to their sex itself. Here is the regression report:

	Estimate	Std. Error	t value	p value
Intercept	35501	2163	16.41	0.0001
sexM	4735	2605	1.82	0.0714

The estimated difference in earnings between men and women is $4700 ± 5200 – not at all precise.

Another model can be used to take into account the worker’s experience, using age as a proxy:

	Estimate	Std. Error	t value	p value
Intercept	14970	3912	3.83	0.0002
sexM	2354	2338	1.01	0.3200
age	594	99	6.02	0.0001

Earnings go up by $600 ± 200 for each additional year of age. The model suggests that part of the difference between the earnings of men and women at this trucking company is due to their age: women tend to be younger than men. The confidence interval on the earnings difference is very broad – $2350 ± 4700 – so broad that the sample doesn’t provide much evidence for any difference at all.

One issue is whether the age dependence of earnings is just a mask for discrimination. To check out this possibility, fit another model that looks at the age dependence separately for men and women:

	Estimate	Std. Error	t value	p value
Intercept	17178	8026	2.14	0.0343
sexM	−443	9174	−0.05	0.9615
age	530	225	2.35	0.0203
sexM:age	79	251	0.32	0.7530

The coefficient on the interaction term between age and sex is 79 ± 502 – no reason at all to think that it’s different from zero. So, evidently, both women and men show the same increase in earnings with age.

Notice that in this last model the coefficient on sex itself has reversed sign from the previous models: Simpson’s paradox. But note also that the confidence interval is very broad: −443 ± 18348. Since the confidence interval includes zero, there is not good evidence to conclude that the coefficient is distinguishable from zero.

The broad confidence interval stems from the multi-collinearity between age and sex and their interaction term. As discussed in Section 12.6, sometimes it is necessary to leave out model terms in order to get reliable results.

Example: SAT Scores and Spending, revisited

The example in Section 10.6 used data from 50 US states to try to see how teacher salaries and student-teacher ratios are related to test scores. The model used was sat ~ salary+ratio + frac, where frac is a covariate – what fraction of students in each state took the SAT. To interpret the results properly, it’s important to know the confidence interval of the coefficients:

	Estimate	Std. Error	t value	p value
Intercept	1057.9	44.3	23.86	0.0000
salary	2.5	1.0	2.54	0.0145
ratio	−4.6	2.1	−2.19	0.0339
frac	−2.9	0.3	−12.76	0.0000

The confidence interval on salary is 2.5 ± 2.0, leaving little doubt that the data support the idea that higher salaries are associated with higher test scores. Higher student-faculty ratios seem to be associated with lower test scores. You can see this because the confidence interval on ratio, −4.6 ± 4.2, doesn’t cover zero. The important role of the covariate frac is also confirmed by its tight confidence interval away from zero.

Collecting more data would allow more precise estimates to be made. For instance, collecting data over 4 years would reduce the standard errors in half, although what the estimates would be with the new data cannot be known until the analysis is done.

Confidence intervals for very small samples.

When you have data with a very small n, say n < 20, a multiplier of 2 can be misleading. The reason has to do with how well a small sample can be assumed to represent the population. The correct multiplier depends on the difference between the sample size n and the number of model coefficients m:

n−m	1	2	3	5	10	15
Multiplier for 95% confidence level	12.7	4.3	3.2	2.6	2.2	2.1

For example, if you fit the running time versus age and sex model to 4 cases, the appropriate multiplier should be 12.7, not even close to 2.

12.4 Confidence in Predictions

When a model value is used for making a prediction, the coefficients themselves aren’t of direct interest; it’s the prediction that counts. Just as the precision of a coefficient can be established, each prediction has a precision that can be described using a confidence interval.

To illustrate, consider making a prediction of a child’s adult height when you know the heights of the mother and father and the child’s sex. Using Galton’s data from the 19th century, a simple and appropriate model is height ~ sex + mother + father.

	Estimate	Std. Error	t value
Intercept	15.3448	2.7470	5.59
sexM	5.2260	0.1440	36.29
mother	0.3215	0.0313	10.28
father	0.4060	0.0292	13.90

Now consider a hypothetical man – call him Bill – whose mother is 67 inches tall and whose father is 69 inches tall. According to the model formula, Bill’s predicted height is 15.3448 + 5.226 + 0.3215 × 67 + 0.406 × 69 = 70.13 inches.

One way to calculate a confidence interval on a model value is similar to bootstrapping. Conduct many trials on resampled data. For each trial, fit the model and calculate the model value from the resulting coefficients. The spread of the various model values from the trials gives the standard error and confidence interval. For Bill, the 95% confidence interval on his model height works out to be 70.13 ± 0.27 inches: a precision of about a quarter of an inch. This high precision reflects the small standard errors of the coefficients which arise in turn from the large amount of data used to fit the model.

It is wrong to interpret this interval as saying something about the actual range of heights of men like Bill, that is, men whose mother is 67 inches and father 69 inches. The model-value confidence interval should not be interpreted as saying that 95 percent of such men will have heights in the interval 70.13 ± 0.27. Instead, this interval means that if you were to fit a model based on the entire population – not just the 898 cases in Galton’s data – the model you would fit would likely produce a model value for Bill close to 70.13. In other words, the model-value confidence interval is not so much about the uncertainty in Bill’s height as in what the model has to say about the average for men like Bill.

If you are interested in what the model has to say about the uncertainty the prediction of Bill’s height, you need to ask a different question and compute a different confidence interval. The prediction confidence interval takes into account the spread of the cases around their model values: the residuals. For the model given above, the standard deviation of the residuals is 2.15 inches – a typical person varies from the model value by that amount.

The prediction confidence interval takes into account this case-by-case residual to give an indication of the range of heights into which the actual value is likely to fall. For men like Bill, the 95% prediction interval is 70.13 ± 4.24 inches. This is much larger than the interval on the model values, and reflects mainly the size of the residual of actual cases around their model values.

Example: Catastrophe in Grand Forks

In April 1997, there was massive flooding on the Red River in Minnesota and North Dakota, states in the northern US, due to record setting winter snows. The towns of Grand Forks and East Grand Forks were endangered and the story was in the news. I remember hearing a news report saying that the dikes in Grand Forks could protect against a flood level of 50 feet and that the National Weather Service predictions were for the river to reach a maximum of 47.5 to 49 feet. To the reporter and the city planners, this was good news. The city had never been better prepared and the preparations were paying off. To me, even knowing nothing about the area, the report was a sign of trouble. What kind of confidence interval was this 47.5 to 49? No confidence level was reported. Was it at a 50% level, was it at a 95% level? Was it a confidence interval on the model values alone or did it include the residuals from the model values? Did it take into account the extrapolation involved in handling record-setting conditions? Nothing in the news stories gave any insight into how precise previous predictions had been.

In the event, the floods reached 54.11 feet in Grand Forks, overtopping the dikes and inundating both towns. Damage was estimated to be more than $1 billion, a huge amount given the small population of the area. In the aftermath of the flood, the mayor of East Grand Forks said, understandably, “They [the National Weather Service] missed it, and they not only missed it, they blew it big.” The Grand Forks city engineer lamented, “with proper advance notice we could have protected the city to almost any elevation . . . if we had known, I’m sure that we could have protected a majority of the city.”

But all the necessary information was available at the time. The forecast would have been accurate if a proper prediction confidence interval had been given. It turns out that the quoted 47.5 to 49 foot interval was not a confidence interval at all – it was the range of predictions from a model under two different scenarios, with and without ongoing precipitation.

Looking back on the history of predictions from the National Weather Service, the typical residual was about 11% of the prediction. Thus, a reasonable 95% confidence interval might have been ±22%, or, translated to feet, 48 ± 10 feet. Had this interval been presented, the towns might have been better prepared for the actual level of 54.11 feet, well within the confidence band.

Whether a 95% confidence level is appropriate for disaster planning is an open question and reflects the balance between the costs of preparation and the potential damage. If you plan using a 95% level, the upper boundary of the interval will be exceeded something like 2.5% of the time. This might be acceptable, or it might not be.

What shouldn’t be controversial is that confidence intervals need to come with a clear statement of what they mean. For disaster planning, a model-value confidence interval is not so useful – it’s about the quality of the model rather than the uncertainty in the actual outcome.

[Much of this example is drawn from the account by Roger Pielke (Jr. 1999).]

12.5 A Formula for the Standard Error

When you do lots of simulations, you start to see patterns. Sometimes these patterns are strong enough that you can anticipate the result of a simulation without doing it. For example, suppose you generate two random vectors A and B and calculate their correlation coefficient: the cosine of the angle between them. You will see some consistent patterns. The distribution of correlation coefficients will have zero mean and it will have standard deviation of 1/√n.

Traditionally, statisticians have looked for such patterns in order save computational work. Why do a simulation, repeating something over and over again, if you can anticipate the result with a formula?

Such formulas exist for the standard error of a model coefficient. They are implemented in statistical software and used to generate the regression report. Here is a formula for computing the standard error of the coefficient on a model vector B in a model with more than one explanatory vector, e.g., A ~ B + C + D. You don’t need to use this formula to calculate standard errors; the software will do that. The point of giving the formula is to show how the standard error depends on features of the model, so that you can strategize about how to design your models to give suitable standard errors.

\[ \mbox{standard error of B coef.} = |\mbox{residuals}|\frac{1}{|\mbox{B}|}\ \frac{1}{\sin( \theta )}\ \frac{1}{\sqrt{n}}\ \sqrt{\frac{n}{n-m}} .\]

There are five components to this formula, each of which says something about the standard error of a coefficient:

|residuals| – The standard error is directly proportional to the size of the residuals.
1/|B| – The length of the model vector reflects the units of that variable or, for the indicator vector for a categorical variable, how many cases are at the corresponding level.
1/sin(θ) – This is the magnifying effect of collinearity. θ is the angle between explanatory vector B and all the other explanatory vectors. More precisely, it is the angle between B and the vector that would be found by fitting B to all the other explanatory vectors. When θ is 90°, then sin(θ)=1 and there is no collinearity and no magnification. When θ = 45°, the magnification is only 1.4. But for strong collinearity, the magnification can be very large: when θ = 10°, the magnification is 5.8. When θ = 1°, magnification is 57. For θ = 0, the alignment becomes a matter of redundancy, since B can be exactly modeled by the other explanatory variables. Magnification would be infinite, but statistical software will identify the redundancy and eliminate it.
1/√n – This reflects the amount of data. Larger samples give more precise estimates of coefficients, that is, a smaller standard error. Because of the square-root relationship, quadrupling the size of the sample will halve the size of the standard error. To improve the standard error by ten-fold requires a 100-fold increase in the size of the sample.
√(n/(n-m)) – The fitting process chooses coefficients that make the residuals as small as possible consistent with the data. This tends to underestimate the size of residuals – for any other estimate of the coefficients, even one well within the confidence interval, the residuals would be larger. This correction factor balances this bias out. n is, as always, the number of cases in the sample and m is the number of model vectors. So long as m is much less than n, which is typical of models, the bias correction factor is close to 1.

The formula suggests some ways to build models that will have coefficients with small standard errors.

Use lots of data: large n.
Include model terms that will account for lots of variation in the response variable and thereby produce small residuals.
But avoid collinearity.

The next section emphasizes the problems that can be introduced by collinearity.

12.6 Confidence and Collinearity

One of the key decisions that a modeler makes is whether to include an explanatory term; it might be a main term or it might be an interaction term or a transformation term.

The starting point for most people new to statistics might be summarized as follows:

Methodologically Ignorant Approach. Include just one explanatory variable.

Most people who work with data can understand tabulations of group means (in modeling language, A ~ 1 + G, where G is a categorical variable) or simple straight-line models (A ~ 1 + B, where B is a quantitative variable.)

At this point, the reader of this book should understand how to include in a model multiple explanatory variables and terms such as interactions. When people first learn this, they typically start putting in lots of terms:

Greedy Approach. Include everything, just in case.

The idea here is that you don’t want to miss any detail; the fitting technology will untangle everything.

Perhaps the word “greedy” is already signalling the problem in a metaphorical way. The poet Horace (65-8 BC) wrote, “He who is greedy is always in want.” Or Seneca (1st century AD), “To greed, all nature is insufficient.”

The flaw with the greedy approach to statistical modeling is not a moral fault. If adding a term improves your model, go for it! The problem is that, sometimes, adding a term can hurt the model by dramatically inflating standard errors.

To illustrate, consider a set of models of wage from the Current Population Survey 85 dataset: CPS85. A relatively simple model might take just the worker’s education into account: wage ~ 1 + educ:

	Estimate	Std. Error	t value	p value
Intercept	−0.746	1.045	−0.71	0.4758
educ	0.750	0.079	9.53	0.0000

The coefficient on educ says that a one-year increase in education is associated with a wage that is higher by 75 cents/hour. (Remember, these data are from the mid-1980s.) The standard error is 8 cents/hour per year of education, so the confidence interval is 75 ± 16 cents/hour per year of education.

A slightly more elaborate model includes age as a covariate. This might be important because education levels typically are lower in older workers, so a comparison of workers with the same level of education ought to hold age constant. A simple adjustment will take that into account. Here’s the regression table on the model wage ~ 1 + educ + age:

	Estimate	Std. Error	t value	p value
Intercept	−5.534	1.279	−4.33	0.0001
educ	0.821	0.077	10.66	0.0001
age	0.105	0.017	6.11	0.0001

In this new model, the coefficient on educ slightly from 75 to 82 cents/hour per year of education while leaving the standard error more or less the same.

Of course, wages also depend on experience. Every year of additional education tends to cut out a year of experience. Here is the regression report from the model wage ~ 1 + educ + age + exper:

	Estimate	Std. Error	t value	p value
Intercept	−4.770	7.042	−0.68	0.4985
educ	0.948	1.155	0.82	0.4121
age	−0.022	1.155	−0.02	0.9845
exper	0.128	1.156	0.11	0.9122

Look at the regression table carefully. The standard errors have exploded! The confidence interval on educ is now 95 ± 231 cents/hour per year of education – a very imprecise estimate. Indeed, the confidence interval now includes zero, so the model is consistent with the skeptic’s claim that education has no effect on wages, once you hold constant the level of experience and age of the worker.

A better interpretation is that greed has gotten the better of the modeler. The large standard errors in this model reflect a deficiency in the data: the multi-collinearity of exper with age and educ as described in in the example in Section 8.4.

A simple statement of the situation is this:

Collinearity and multi-collinearity cause model coefficients to become less precise – they increase standard errors.

This doesn’t mean that you should never include model terms that are collinear or multi-collinear. If the precision of your estimates is good enough, even with the collinear terms, then there is no problem. You, the modeler, can judge if the precision is adequate for your purposes.

The estimate 95 ± 231 cents/hour is probably not precise enough for any reasonable purpose. Including the exper term in the model has made the entire model useless, not just the exper term, but the other terms as well! That’s what happens when you are greedy.

The good news is that you don’t need to be afraid of trying a model term. Use the standard errors to judge when your model is acceptable and when you need to think about dropping terms due to collinearity.

Aside: Redundancy and Multi-collinearity

Redundancy can be seen as an extreme case of multi-collinearity. So extreme that it renders the coefficients completely meaningless. That’s why statistical software is written to delete redundant vectors. With multi-collinearity, things are more of a judgment call. The judgment needs to reside in you, the modeler.

12.7 Confidence and Bias

The margin of error tells you about the precision of a coefficient: how much variation is to be anticipated due to the random nature of sampling. It does not, unfortunately, tell you about the accuracy of the coefficient; how close it is to the “true” or “population” value.

A coefficient makes sense only within the context of a model. Suppose you fit a model A ~ B + C. Then you think better of things and look at the model A ~ B + C + D. Unless variable D happens to be orthogonal to B and C, the coefficients on B and C are going to change from the first model to the second.

If you take the point of view that the second model is “correct,” then the coefficients you get from the first model are wrong. That is, the omission of D in the first model has biased the estimates of B and C.

On the other hand, if you think that the model A ~ B + C reflects the “truth,” then the coefficients on B and C from A ~ B + C + D are biased.

The margin of error from any model tells you nothing about the potential bias. How could it? In order to measure the bias you would have to know the “correct” or “true” model.

The issue of bias often comes down to which is the correct set of model terms to include. This is not a statistical issue – it depends on how well your model corresponds to reality. Since people disagree about reality, perhaps it would be best to think about bias with respect to a given theory of how the world works. A model that produces unbiased coefficients according to your theory of reality might give biased coefficients with respect to someone else’s theory. Avoiding bias is a difficult matter and it’s hard to know when you have succeeded. A very powerful but challenging strategy is to intervene to make your system simpler, so that every modeler’s theories can agree. See Chapter 18.