Generalizing Inference
Objectives: Cover the genuinely useful settings of a traditional intro stats course while …
- saving time, so that we can choose to cover other topics: e.g. covariation, causality, decision-making, …
- setting things up for more advanced settings: multiple regression, machine learning models, classification, …
- simplifying the framework
- one set of formulas
- simple (or trivial) critical values
- avoiding undue emphasis on p values
- keeping an emphasis on prediction
Recap:
- Make graphics about data, with annotations always presented in the context of data.
- Rather than calculating “statistics” (e.g. mean, medians, …) build a prediction model
- Focus on effect size in natural units rather than dimensionless quantities such as r or \(\chi^2\) or \(p\).
Now … how to set up the inference calculations.
Variance: How much variation?
We focus on the response variable …
Average pairwise square differences between values.
\[\frac{1}{n (n-1)}\sum_{i \neq j} |x_i - x_j|^2 = 2\ \mbox{Var}(x)\]
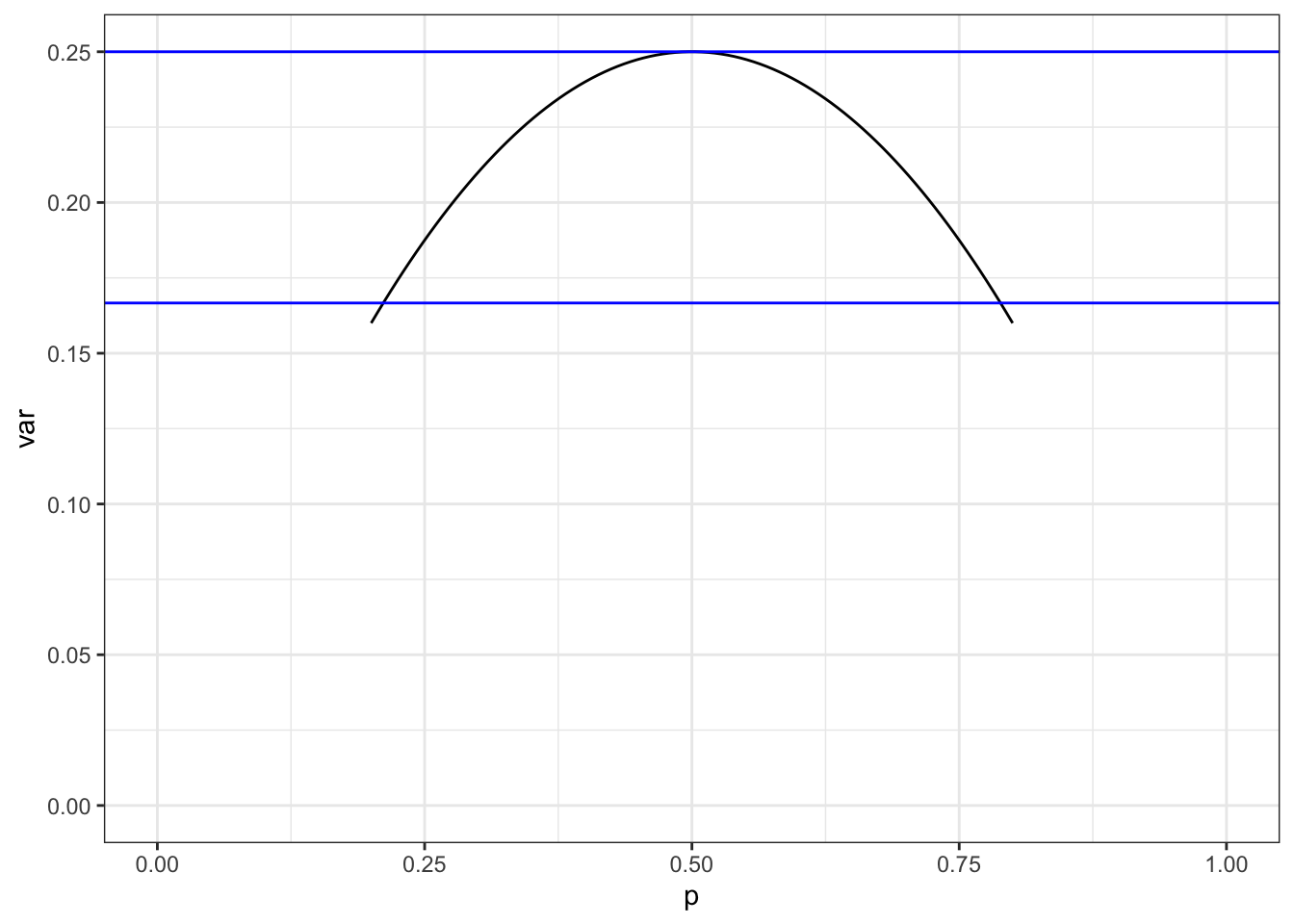
Estimating variance by eye:
- more-or-less normal: find interval covering the central 2/3 of the data. (Thus, 1/6 is left out at either end.) Divide by 2 and square to get the variance.
- Two discrete levels: \(\Delta^2 p(1-p)\)
- \(p (1-p) \approx 1/4\) when levels are more or less equally populated
- \(p (1-p) \approx 1/6\) when levels are noticeably unequally populated.
Model values: How much has been explained?

Basic discernibility
Note that I’m being much more mathy here than I would in teaching a typical class. The audience here is professional mathematicians, hence likely not too scared by algebraic notation.
- Is there any discernible relationship between the response and explanatory variables revealed by the model?
- Inputs from the model: \(v_r\), \(v_m\), \(n\), and degrees of flexibility \(^\circ{\cal F}\)
- Output: \[\mbox{F} = \frac{n - (^\circ{\cal F} + 1)}{^\circ{\cal F}} \frac{v_m}{v_r - v_m}\] … or, equivalently, … \[\mbox{F} = \frac{n - (^\circ{\cal F} + 1)}{^\circ{\cal F}} \frac{R^2}{1 - R^2}\]
- Interpretation: Is F \(\gtrapprox 4\)?. Then a relationship is discernible.
Confidence intervals (when \(^\circ\!{\cal F} = 1\))
When \(^\circ\!{\cal F} = 1\), there is only one explanatory variable and the modeling situation is one of these:
- difference between two groups
- slope of a regression line
Either way, there is only one effect size: the difference or slope.
- Inputs:
- Effect size B
- F
- Output:
- Margin of error is \(\pm \mbox{B} \sqrt{4 / \mbox{F}}\)
- Interpretation:
- We wouldn’t be at all surprised if a much, much bigger study revealed an effect size within the confidence interval. - If we are comparing our study to another study, we’re only justified in claiming a contradiction when the two confidence intervals don’t overlap.
- Do we really need to refer to populations?
Note that when \(^\circ\!{\cal F} \geq 2\), there is either more than one explanatory variable or more than one group in that explanatory variable or a non-straight-line regression (e.g. a polynomial). In none of these cases can the margin of error be deduced directly from F due to one or more of:
- effect size not constant
- multiple effect sizes
- collinearity among explanatory variables
Instead of the simple formula based on F, confidence intervals can be based on a regression table or bootstrapping.
Activity 3
See the handout on R2 showing the same settings as in the previous chapters. You should already have estimated an effect size of the response with respect to the x-axis variable.
- Estimate R2. Hint: This should be easy, though you have to remember to square.
- Pick a few settings of interest. For each:
- Do a significance test using F.
- For settings with \(^\circ\!{\cal F} = 1\), calculate a 95% confidence interval on the effect size.
Standard statistical calculations
We revisit the settings on the handout, showing the F calculation and a standard statistical report.
Setting A: Difference in two proportions 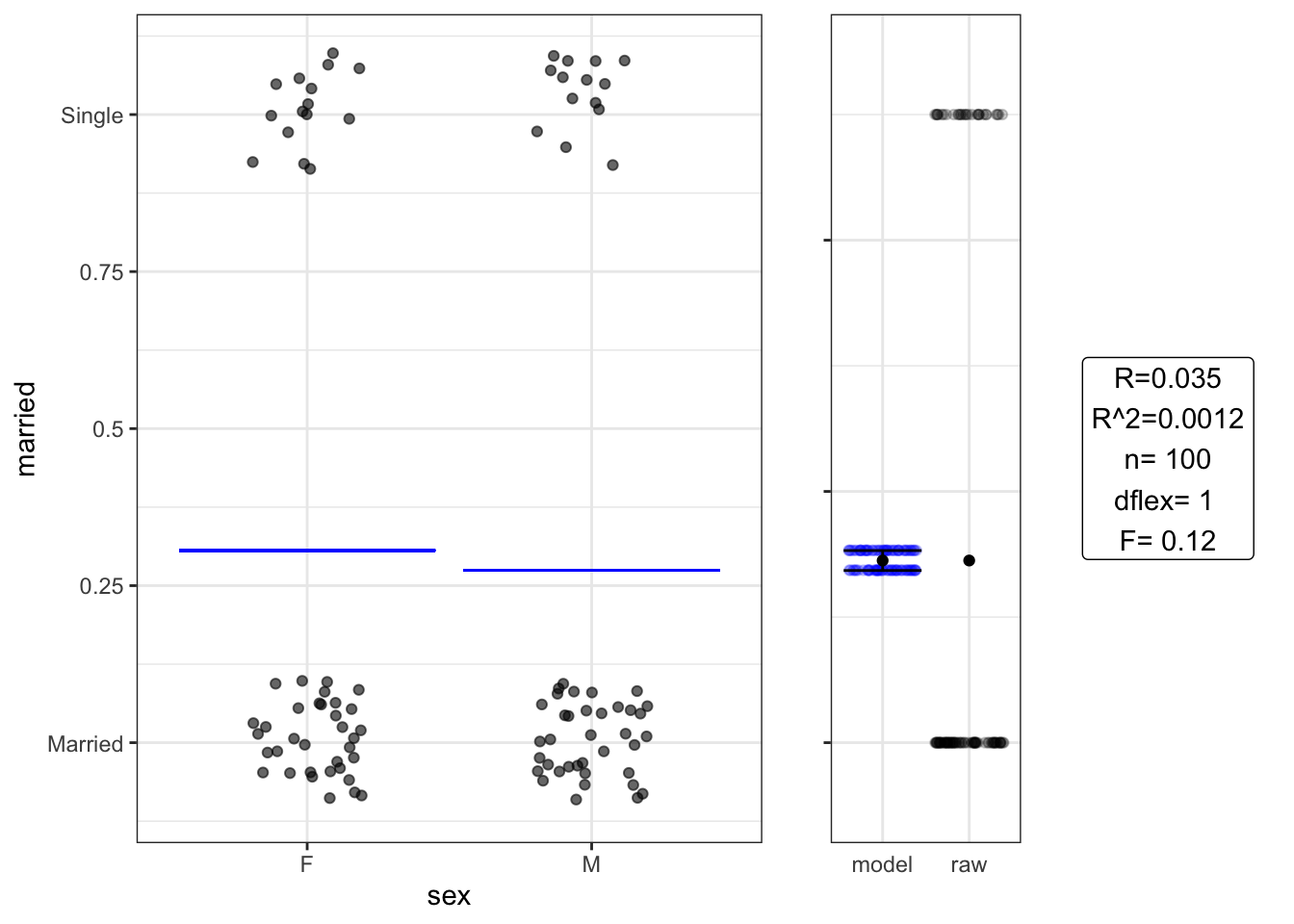
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.310 0.065 4.70 9.3e-06
## sexM -0.032 0.092 -0.34 7.3e-01## Analysis of Variance Table
##
## Response: married
## Df Sum Sq Mean Sq F value Pr(>F)
## sex 1 0.025 0.024974 0.119 0.7308
## Residuals 98 20.565 0.209847No relationship discernable. How much data should we plan for in a repeat study?
Setting B: Difference in two means 
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.6 0.61 16.00 7.7e-29
## unionUnion 1.1 1.30 0.82 4.1e-01## Analysis of Variance Table
##
## Response: wage
## Df Sum Sq Mean Sq F value Pr(>F)
## union 1 19.44 19.439 0.672 0.4144
## Residuals 98 2834.98 28.928Setting D : Slope of a regression line 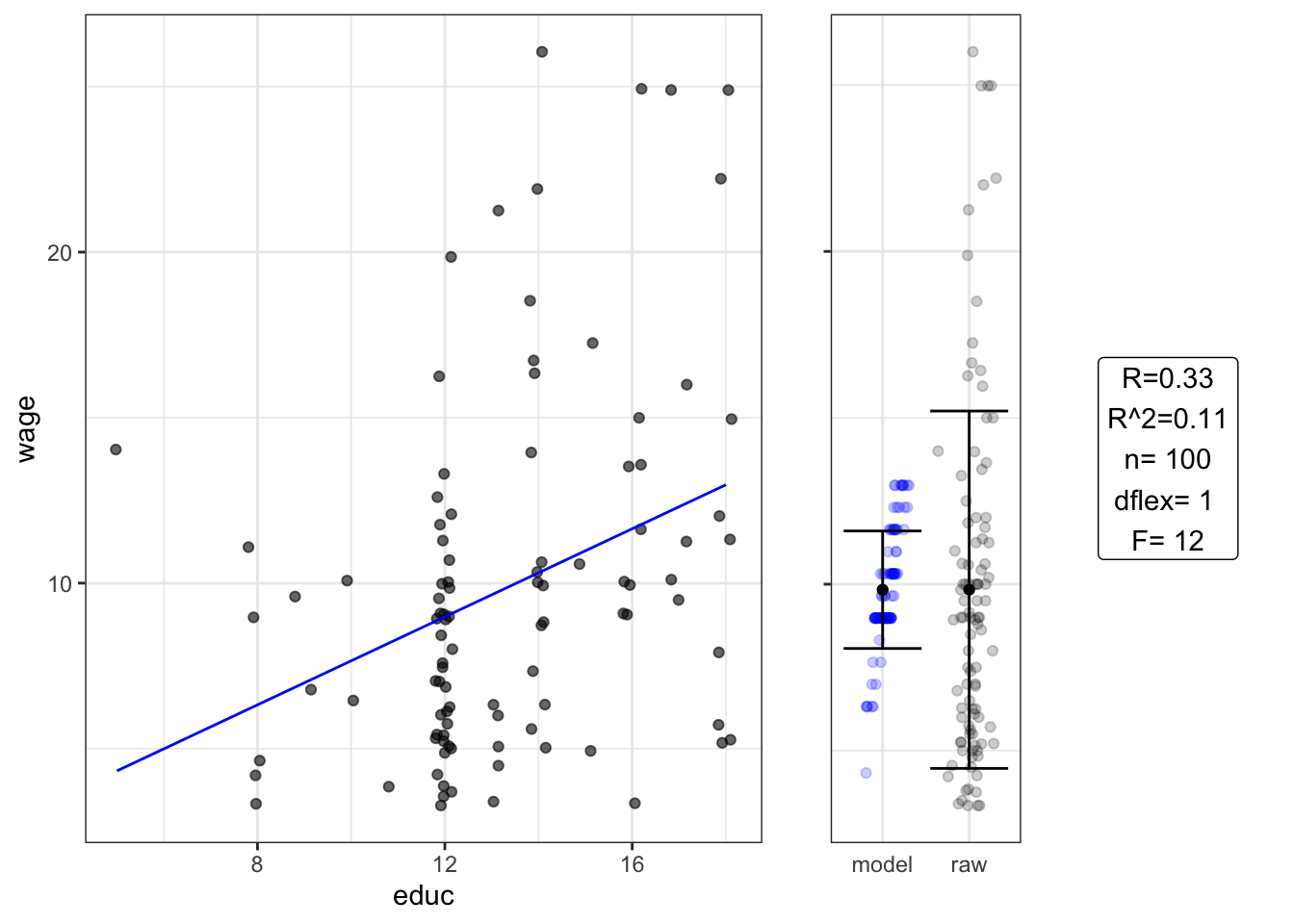
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.00 2.60 0.39 0.70000
## educ 0.66 0.19 3.40 0.00084## Analysis of Variance Table
##
## Response: wage
## Df Sum Sq Mean Sq F value Pr(>F)
## educ 1 308.54 308.537 11.877 0.0008386 ***
## Residuals 98 2545.89 25.978
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Setting H Gets at same thing as chi-squared test 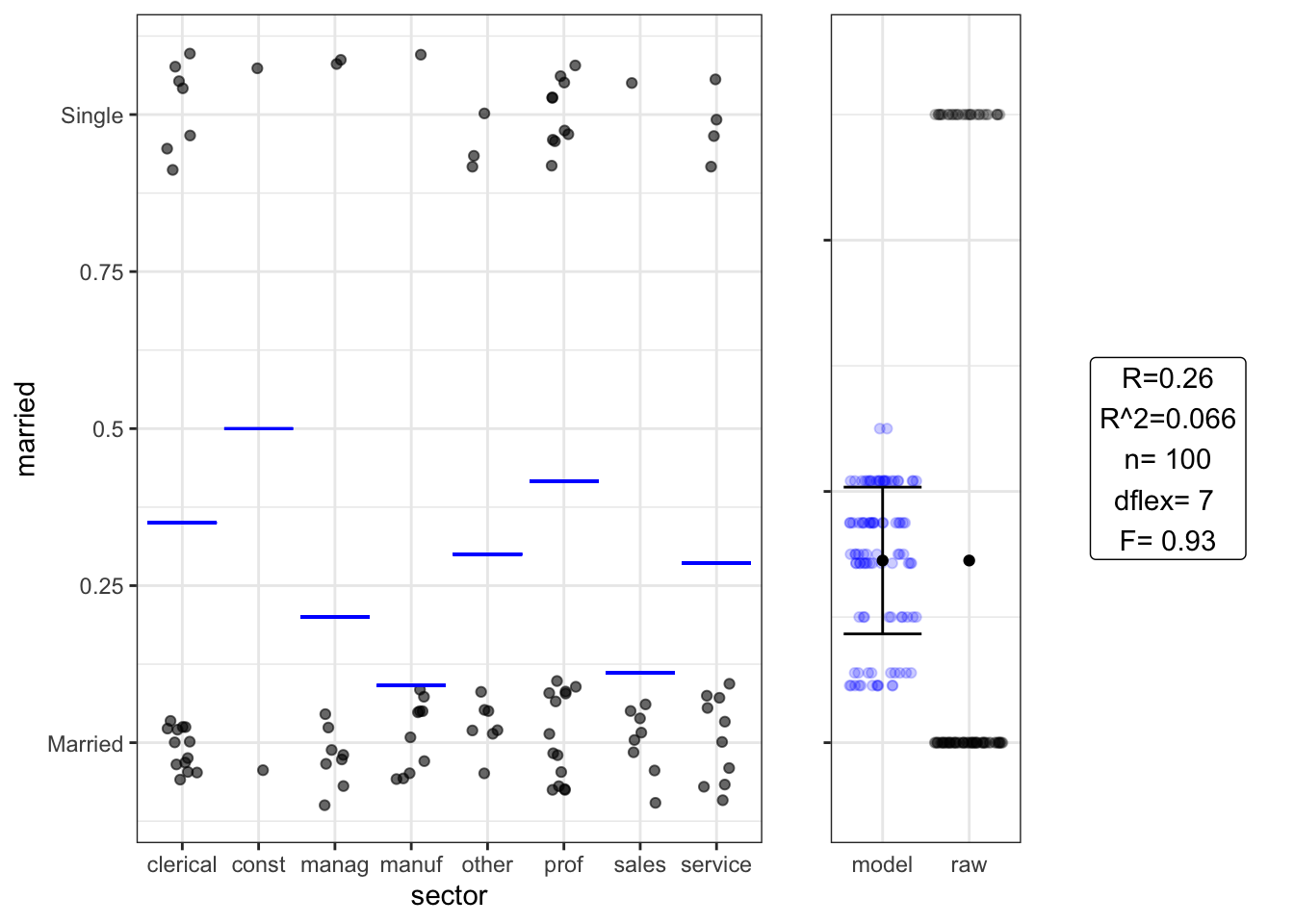
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.350 0.10 3.40 0.00093
## sectorconst 0.150 0.34 0.44 0.66000
## sectormanag -0.150 0.18 -0.85 0.40000
## sectormanuf -0.260 0.17 -1.50 0.13000
## sectorother -0.050 0.18 -0.28 0.78000
## sectorprof 0.067 0.14 0.48 0.63000
## sectorsales -0.240 0.18 -1.30 0.20000
## sectorservice -0.064 0.16 -0.40 0.69000## Analysis of Variance Table
##
## Response: married
## Df Sum Sq Mean Sq F value Pr(>F)
## sector 7 1.3515 0.19308 0.9233 0.4924
## Residuals 92 19.2385 0.20911Not so often reached in intro stats
Setting I: “One-way” ANOVA 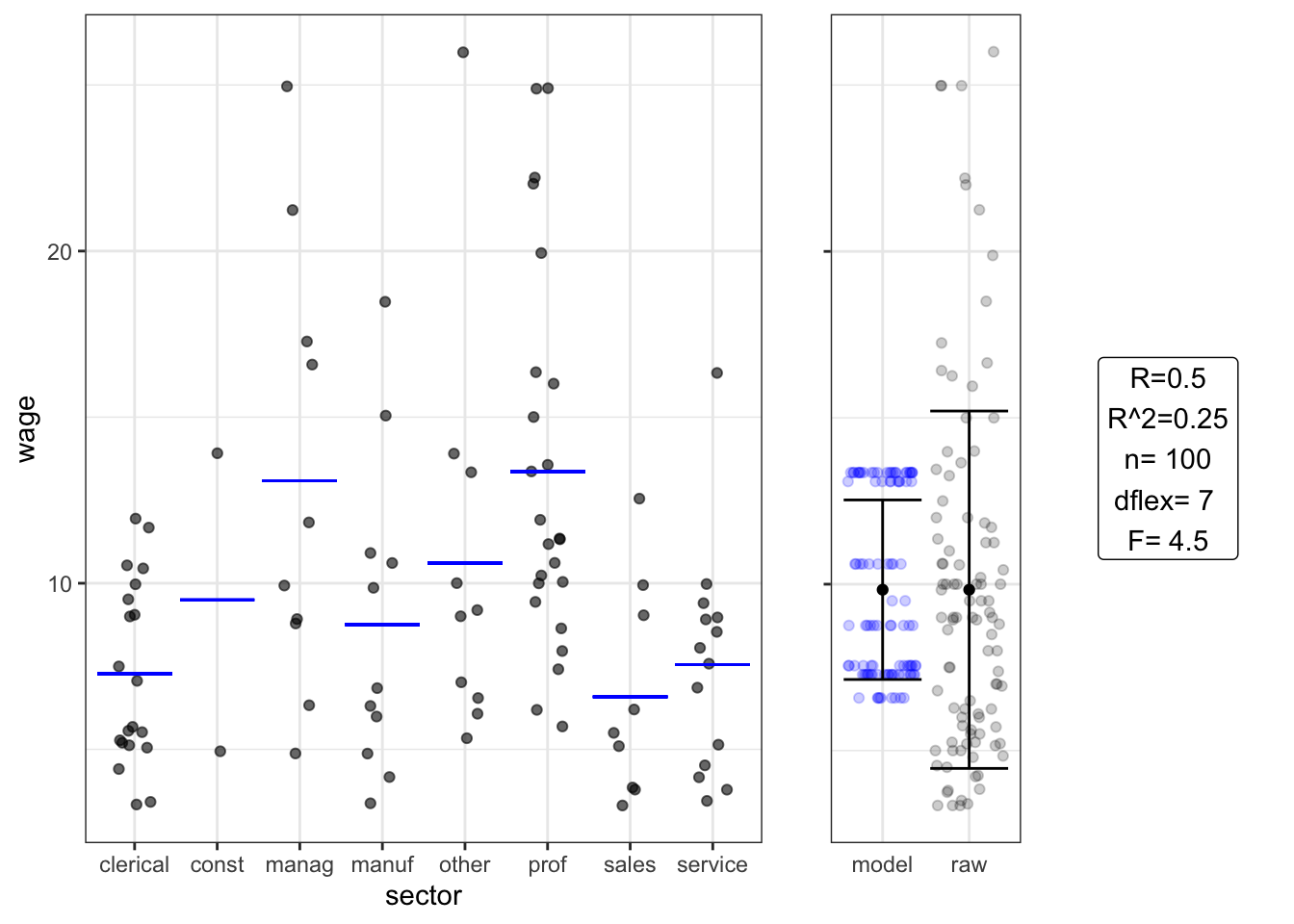
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.30 1.1 6.80 1.2e-09
## sectorconst 2.20 3.6 0.62 5.4e-01
## sectormanag 5.80 1.9 3.10 2.5e-03
## sectormanuf 1.50 1.8 0.82 4.2e-01
## sectorother 3.30 1.9 1.80 7.8e-02
## sectorprof 6.10 1.5 4.20 7.0e-05
## sectorsales -0.70 1.9 -0.36 7.2e-01
## sectorservice 0.27 1.7 0.16 8.7e-01## Analysis of Variance Table
##
## Response: wage
## Df Sum Sq Mean Sq F value Pr(>F)
## sector 7 720.4 102.915 4.4368 0.000275 ***
## Residuals 92 2134.0 23.196
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Setting F “Two-way” ANOVA: wage ~ educ * sex 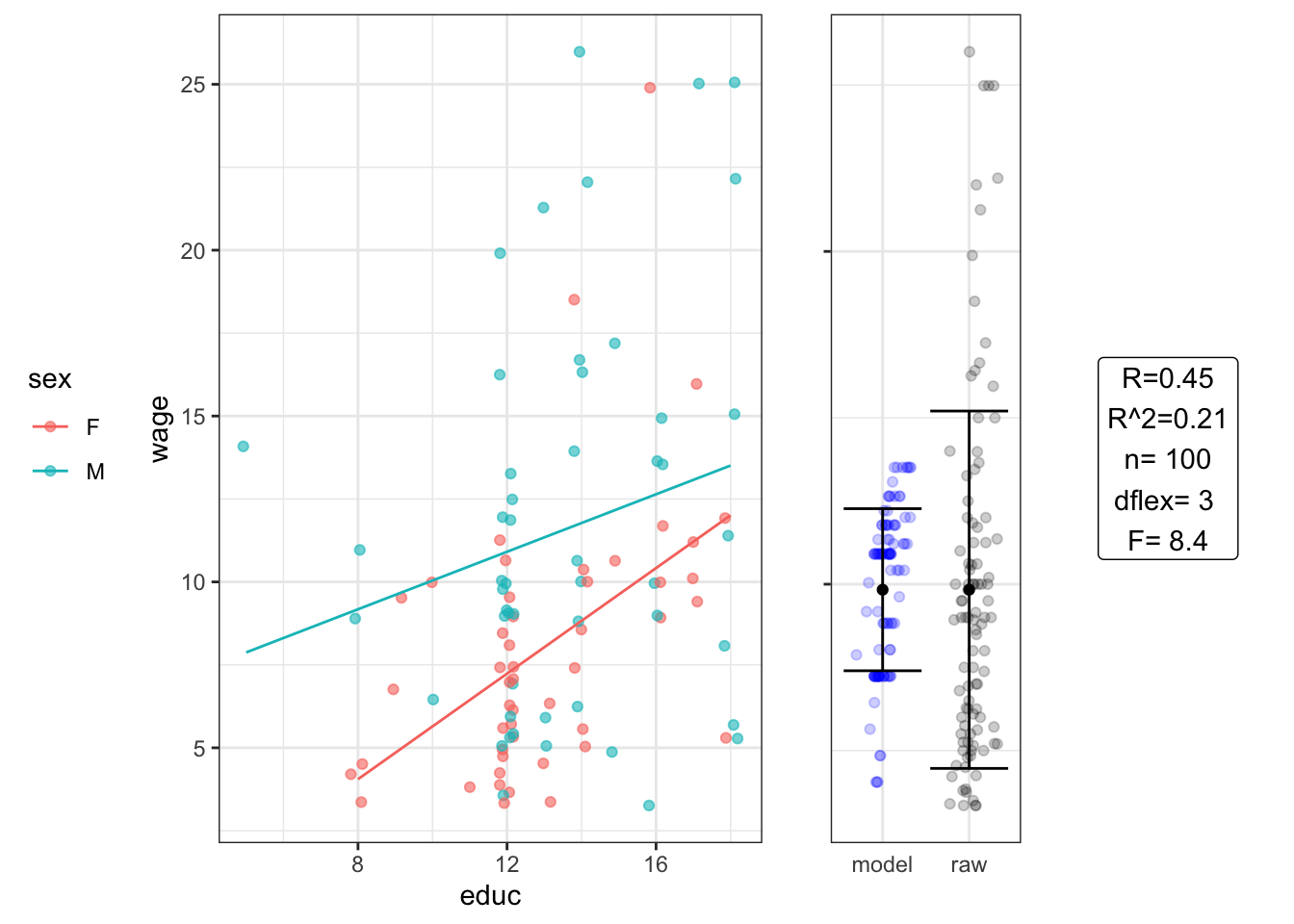
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.30 3.70 -0.63 0.5300
## educ 0.80 0.28 2.80 0.0054
## sexM 8.00 5.00 1.60 0.1100
## educ:sexM -0.36 0.37 -0.97 0.3300## Analysis of Variance Table
##
## Response: wage
## Df Sum Sq Mean Sq F value Pr(>F)
## educ 1 308.54 308.537 13.0642 0.0004816 ***
## sex 1 256.42 256.421 10.8575 0.0013793 **
## educ:sex 1 22.23 22.231 0.9413 0.3343837
## Residuals 96 2267.23 23.617
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Need to compare to results from wage ~ educ + sex
Setting J ANCOVA 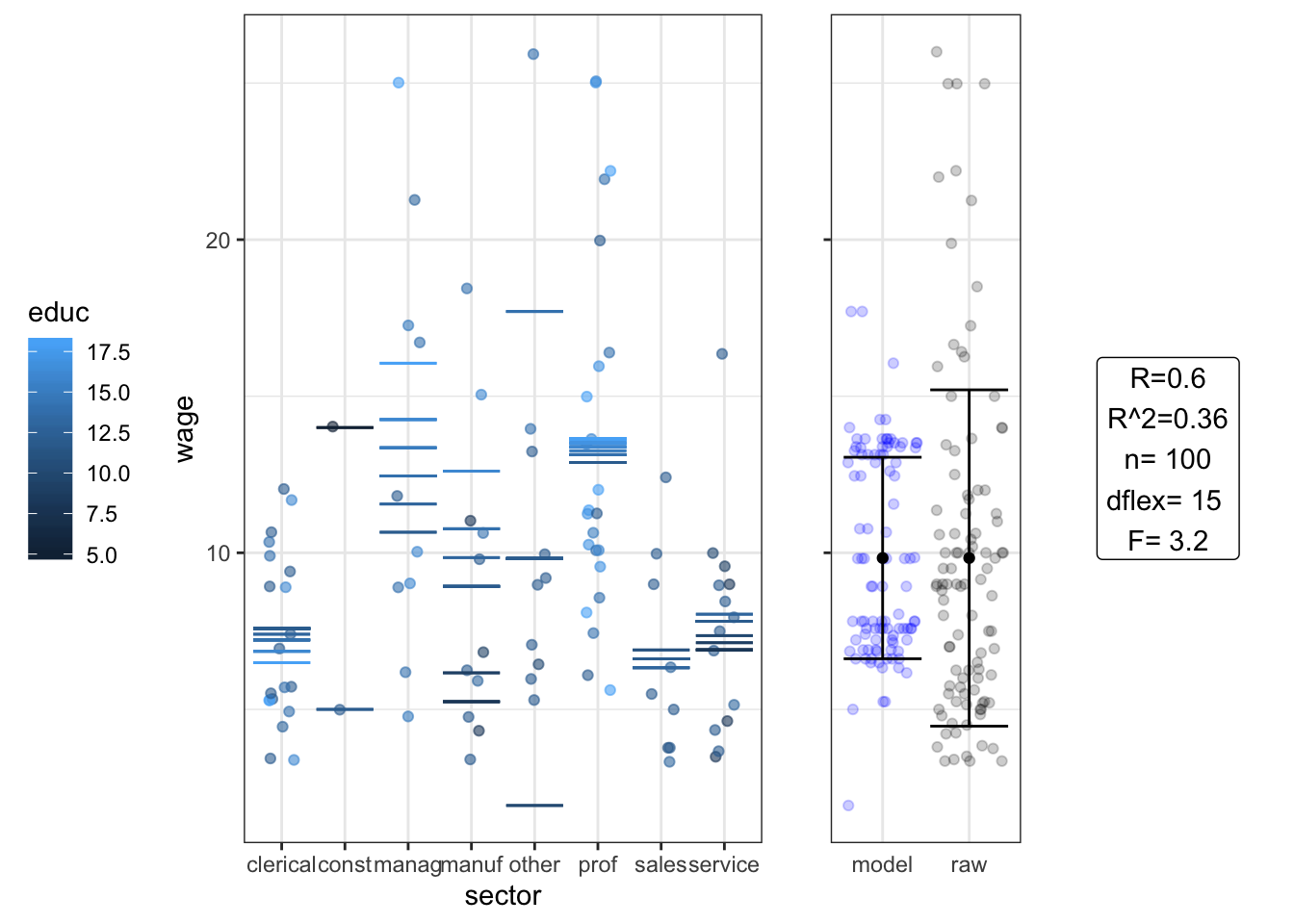
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.80 7.10 1.4000 0.170
## sectorconst 11.00 11.00 0.9500 0.340
## sectormanag -9.90 15.00 -0.6500 0.520
## sectormanuf -12.00 9.90 -1.2000 0.230
## sectorother -47.00 18.00 -2.6000 0.011
## sectorprof 1.60 10.00 0.1600 0.880
## sectorsales 0.27 34.00 0.0078 0.990
## sectorservice -4.70 11.00 -0.4500 0.660
## educ -0.18 0.51 -0.3500 0.720
## sectorconst:educ -1.10 1.10 -1.0000 0.310
## sectormanag:educ 1.10 1.00 1.0000 0.310
## sectormanuf:educ 1.10 0.77 1.4000 0.160
## sectorother:educ 4.10 1.50 2.8000 0.006
## sectorprof:educ 0.31 0.70 0.4400 0.660
## sectorsales:educ -0.10 2.80 -0.0370 0.970
## sectorservice:educ 0.41 0.87 0.4700 0.640## Analysis of Variance Table
##
## Response: wage
## Df Sum Sq Mean Sq F value Pr(>F)
## sector 7 720.40 102.915 4.7248 0.000165 ***
## educ 1 30.84 30.836 1.4157 0.237468
## sector:educ 7 273.53 39.076 1.7940 0.099104 .
## Residuals 84 1829.66 21.782
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1No relationship is discernable. How big an n should we have if we want to have a high likelihood of detecting a relationship? (Hint: We want F > 4.)
Setting G: Accomplishes the same as Three-variable chi-squared: married ~ sex * union 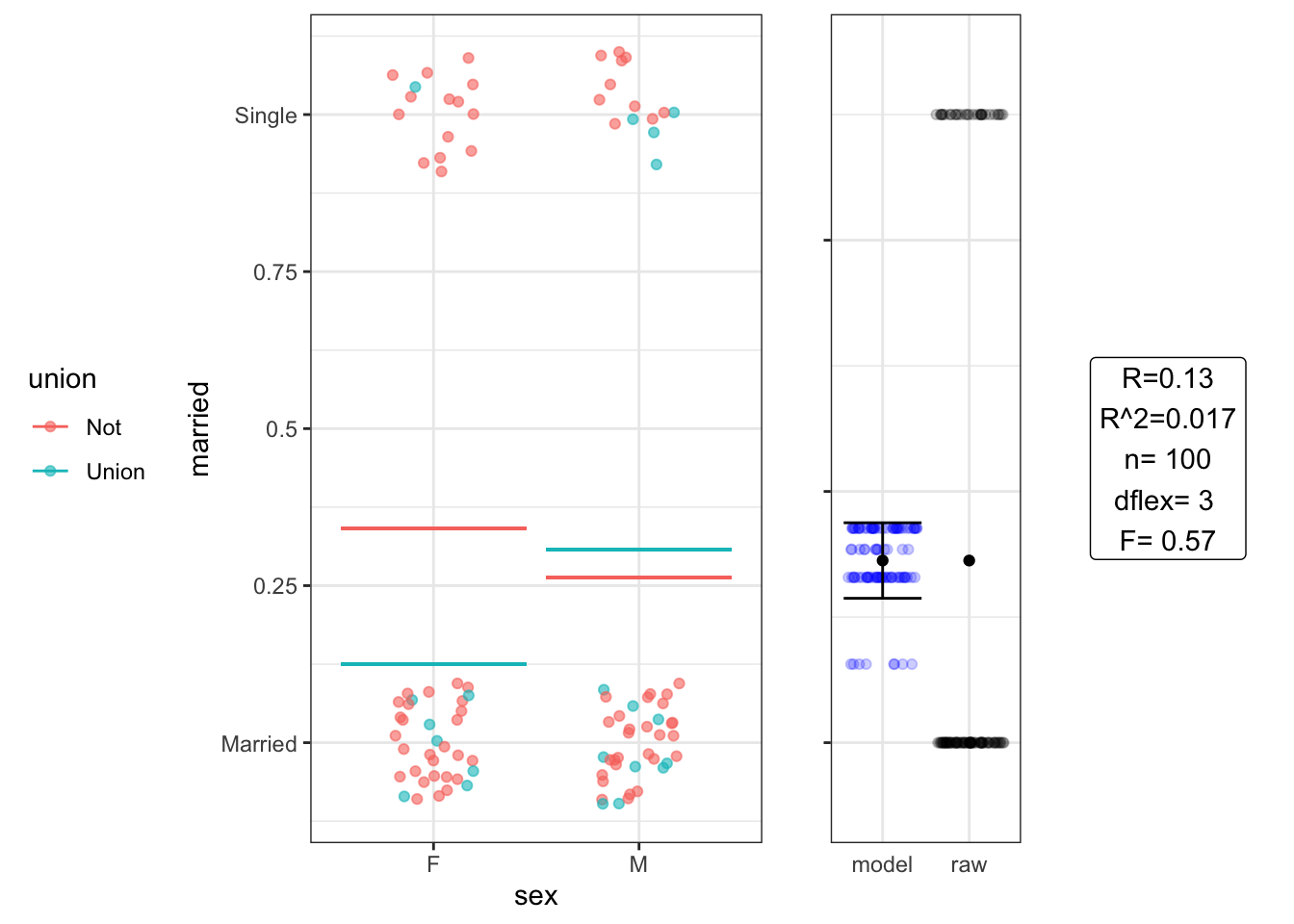
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.340 0.072 4.80 6.8e-06
## sexM -0.078 0.100 -0.76 4.5e-01
## unionUnion -0.220 0.180 -1.20 2.3e-01
## sexM:unionUnion 0.260 0.230 1.10 2.6e-01## Analysis of Variance Table
##
## Response: married
## Df Sum Sq Mean Sq F value Pr(>F)
## sex 1 0.0250 0.024974 0.1185 0.7314
## union 1 0.0632 0.063218 0.3000 0.5852
## sex:union 1 0.2696 0.269644 1.2794 0.2608
## Residuals 96 20.2322 0.210752