Activities C: Tutorial 3

Loading webR...

Activity C.1 The Hill_racing data frame contains winning results for a cross-country running event that is popular in Scotland: Scottish Hill Racing. The time variable gives the winning time in seconds, while distance gives the length of the race (in km). The twist: there is also a climb, given in meters.

Active R chunk C.1 is set up to calculate how fast the winners go, averaging across all the events.

Active R chunk C.1

1

2

3

Hill_racing |>

  model_train(time ~ distance) |>

  conf_interval()

1. Since time is in seconds, and distance in km, what are the units of the coefficient?

km       km / sec       sec / km       sec      

question id: 3-scottish-racing-units

The races are of varying distances, 1.1 to 43 km. It’s to be expected that a person running 43 km will run each kilometer slower than a person running a 2K race. The coefficient (381) tells how much more time in seconds it would take to run an additional kilometer.

2. According to the model, how much time does it take to 10-km race?

Add the intercept and distance coefficient, then multiply by 10. (1700 secs)

Multiply the intercept by 10, then add the distance coefficient. (-1729 secs)

Multiply the distance coefficient by 10, then add the intercept. (3600 secs)[correct]

Multiply the distance coefficient by 10. (3810 secs)

None of the above

question id: 3-scottish-racing-10k

We can also look at the running time as a function of climb, as in Active R chunk C.2.

Active R chunk C.2

1

2

3

Hill_racing |>

  model_train(time ~ climb) |>

  conf_interval()

3. Since time is measured in seconds and climb is measured in meters, what are the units of the coefficient 5.65 in the summary of time ~ climb?

meters       sec       meters / sec       sec / meter      

question id: 3-scottish-racing-climb-units

4. The longest climb in Hill_racing is 2400 meters, about a mile-and-a-half gain in altitude. According to Active R chunk C.2, how long would it take to run the 2400 meter-climb race?

347 + 2400 * 5.66 $\approx$ 4 hours

2400 * 347 + 5.66 $\approx$ 9 days

2400 * 5.66 $\approx$ 4 hours

(347 + 5.6) * 2400 $\approx$ 9 days

question id: 3-scottish-racing-10-climb

To be fair to the race competitors, we should recognize that each even is a combination of a climb and a distance. Active R chunk C.3 includes both distance and climb as explanatory variables.

Active R chunk C.3

1

2

3

Hill_racing |>

  model_train(time ~ distance + climb) |>

  conf_interval()

The summary of time ~ distance + climb says it would take 254 seconds (according to the model) to run a km without any altitude gain, and 2.6 seconds to climb a meter without any distance (which is unphysical). Compare these coefficients to the ones from time ~ distance and time ~ climb and explain in everyday terms why the time ~ distance + climb model shows the runners being both faster in distance and faster in climb.

Activity C.2 In these tutorials, we compute a summary of a single variable using the summarize() wrangling command. To illustrate, let’s find the average height of the (full-grown) children in Galton:

Active R chunk C.4

1

2

Galton |>

  summarize(mean(height))

We use another technology, model_train(), to look at the relationship between (or among) variables. For instance:

Active R chunk C.5

1

2

3

Galton |> 

  model_train(height ~ sex) |>

  conf_interval()

The explanatory variable sex in Active R chunk C.5 is categorical with two levels: F and M. In such a situation, there is only one coefficient corresponding to the explanatory variable. The coefficient print-out calls this sexM, which means that it refers to the males. So, where did the females go?

To investigate, Active R chunk C.6 uses summarize() with a .by= argument to calculate means separately for males and females. (You’ll have to replace ___variable___ with the name of an actual variable.)

Active R chunk C.6

1

2

Galton |>

  summarize(mean(height), .by = ___variable__)

1. What does the (Intercept) coefficient from the model height ~ sex tell us?

The mean height of all the children.

The mean sex.

The mean height of females.

The height when sex has a value of 0.

question id: galton-mean-q1

2. What does the sexM coefficient tell us?

The mean height of the males.

The difference between the average height for all children and the height of the males.

The difference between the average height for all children and the height of the females.

The difference in mean height for the males compared to the females.

question id: galton-mean-q2

3. Whenever R trains a model with a categorical explanatory variable, one of the levels is selected as the reference level. (By default, the level that is first alphabetically is used as the reference level.)

What is the reference level used in the height ~ sex model trained on the Galton data.

F       M       neither      

question id: galton-mean-q3

Demonstrate that the coefficient from y ~ 1 is the mean of y. In the case of a binary variable, the coefficient is the proportion of the category assigned level 1.

Activity C.3 Always fun to work with the penguin data! Active R chunk C.7 computes a simple model of penguin bill length:

Active R chunk C.7

1

2

3

Penguins |>

  model_train(bill_length ~ species) |>

  conf_interval()

1. What is the mean bill length for Chinstrap penguins? (Bill length is measured in cm.)

10.0 inches       47.6 inches       48.8 inches       none of these      

question id: 3-penguins-species-1

2. As always, R selects a reference level for the categorical explanatory variable species. Here’s a summary of height .by species:

Active R chunk C.8

1

2

Penguins |>

  summarize(mean(bill_length), .by = species)

Which species is being used as the reference level in the model specified by bill_length ~ species?

Adelie       Chinstrap       Gentoo       none of these      

question id: 3-penguins-species-2

Activity C.4 A “Null model” is a model without any explanatory variables. For instance, a Null model for penguin bill length has the formula bill_length ~ 1.

Penguins |>
  model_train(bill_length ~ 1) |>
  conf_interval()

# A tibble: 1 × 4
  term         .lwr .coef  .upr
  <chr>       <dbl> <dbl> <dbl>
1 (Intercept)  43.4  44.0  44.6

What does the (Intercept) coefficient from this Null model tell us?

Nothing. It’s a “null” model.

The bill length for a penguin that is 1 year old

The mean of the response variable

None of the above

question id: 3-null-model-1

Activity C.5 Here are two models of the Hill_racing data. Both have time as the response variable and have distance and climb as the explanatory variables. One of them involves an interaction between climb and distance, the other does not.

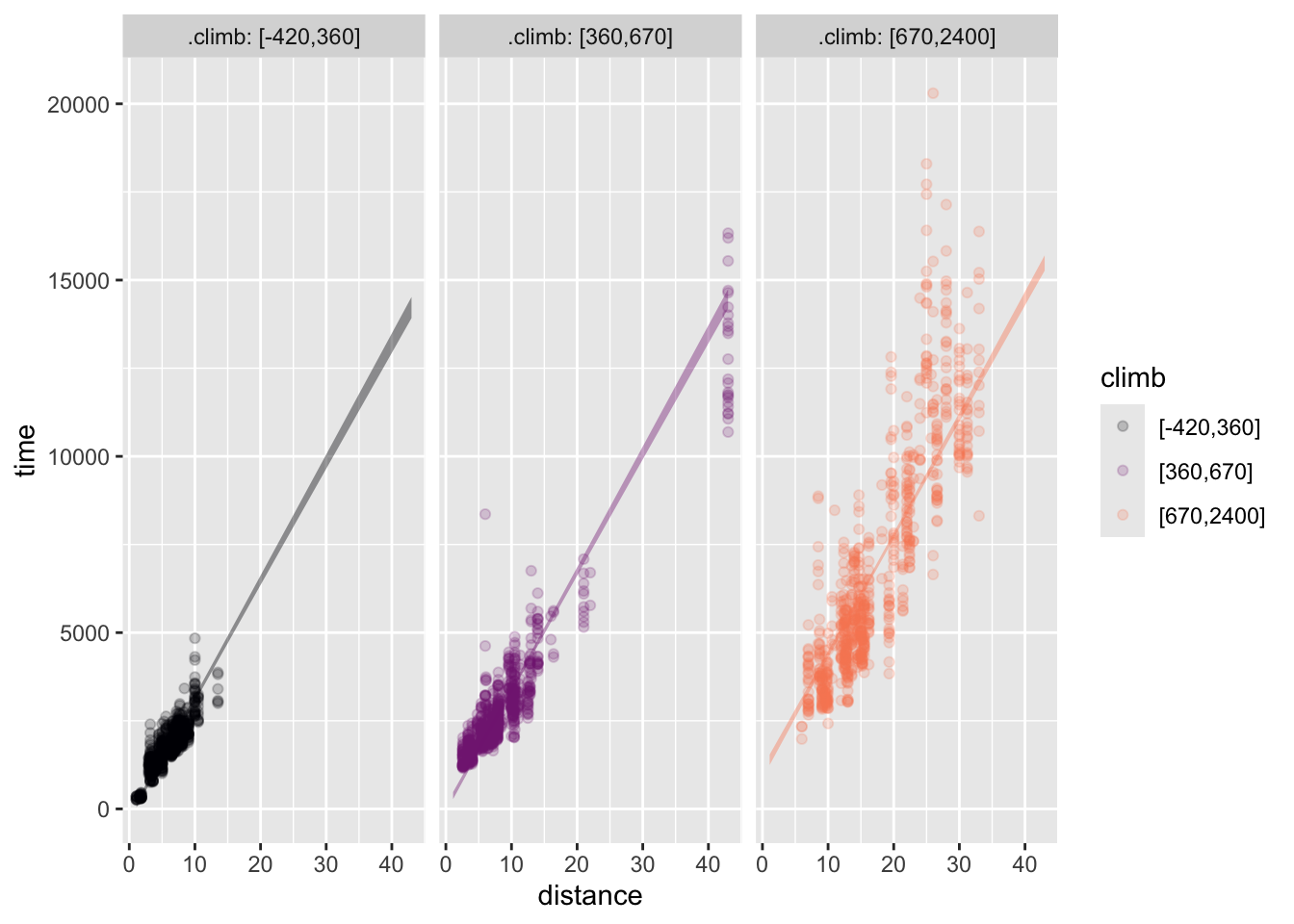
Figure C.1: Two models of the Hill_racing data.

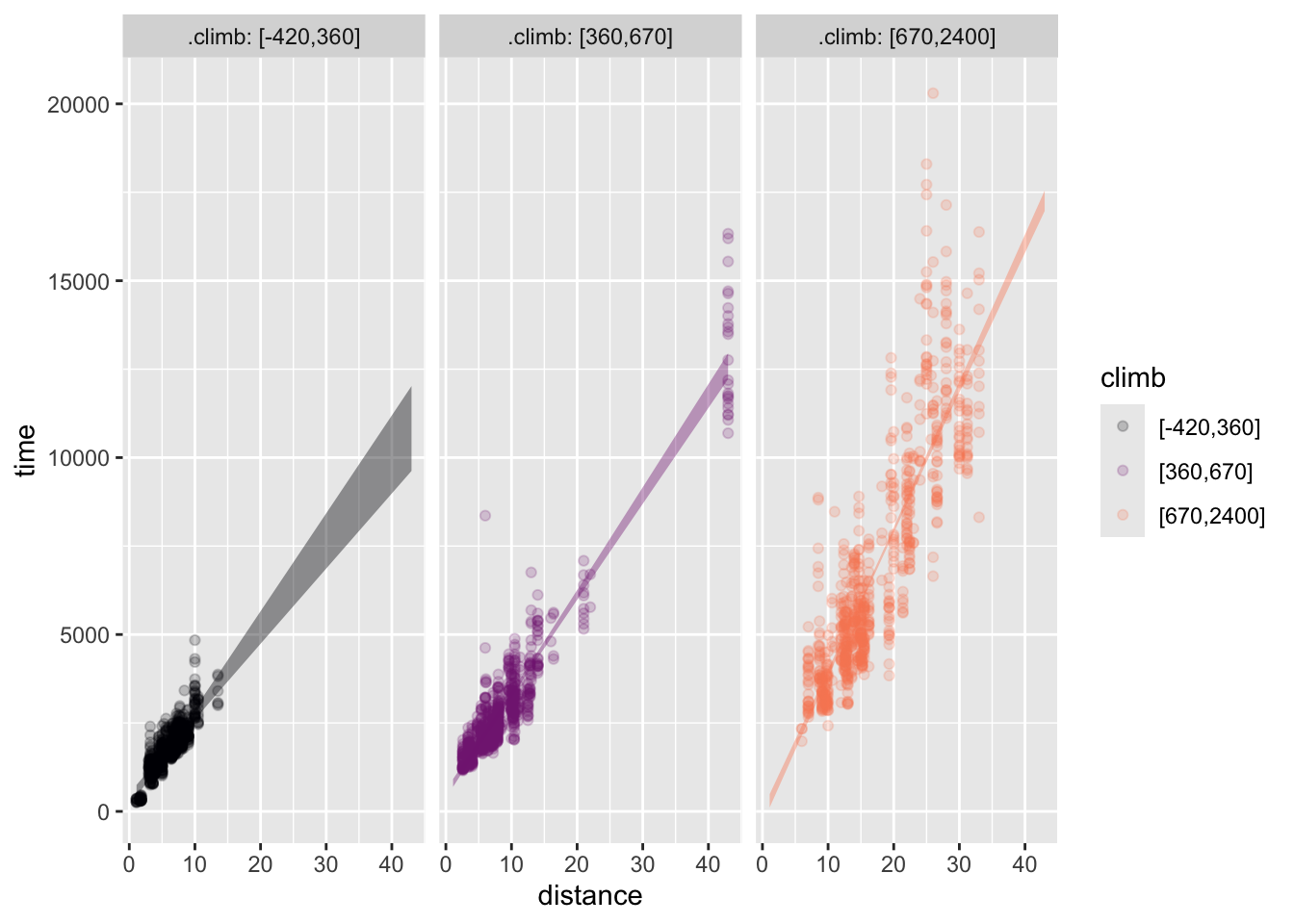
Figure C.2: Two models of the Hill_racing data.

First, identify which model, (a) or (b), involves the interaction term. Then, say whether the interaction model gives longer or shorter race times for the high-climb events. Finally, explain in everyday terms why the interaction model gives a more plausible account of how fast the runners go in low-climb versus high-climb races.

exercises-3.rmarkdown

No answers yet collected

Submit collected answers here