Math 300Z: In-class group activity

Adjusting, visually

These are two graphs of the data from Clock_auction showing the relationship between the winning price and the number of bidders. (I’ve simplified the number of bidders to two categories.) The age of the clock is a covariate. The large dots show the mean age and mean price of the clocks in those auctions with 10 or more bidders versus 9 or fewer bidders.

Code 
Clock_auction <- Clock_auction |> mutate(nbidders = ifelse(bidders >= 10, "10 or more", "9 or fewer"))
Stats <- Clock_auction |> group_by(nbidders) |>
  summarize(mp = mean(price), mage = mean(age))
mod1 <- lm(price ~ nbidders, data=Clock_auction) 

model_plot(mod1, x=age, color=nbidders) |>
  gf_point(mp ~ mage, color=~nbidders, data=Stats, size=3)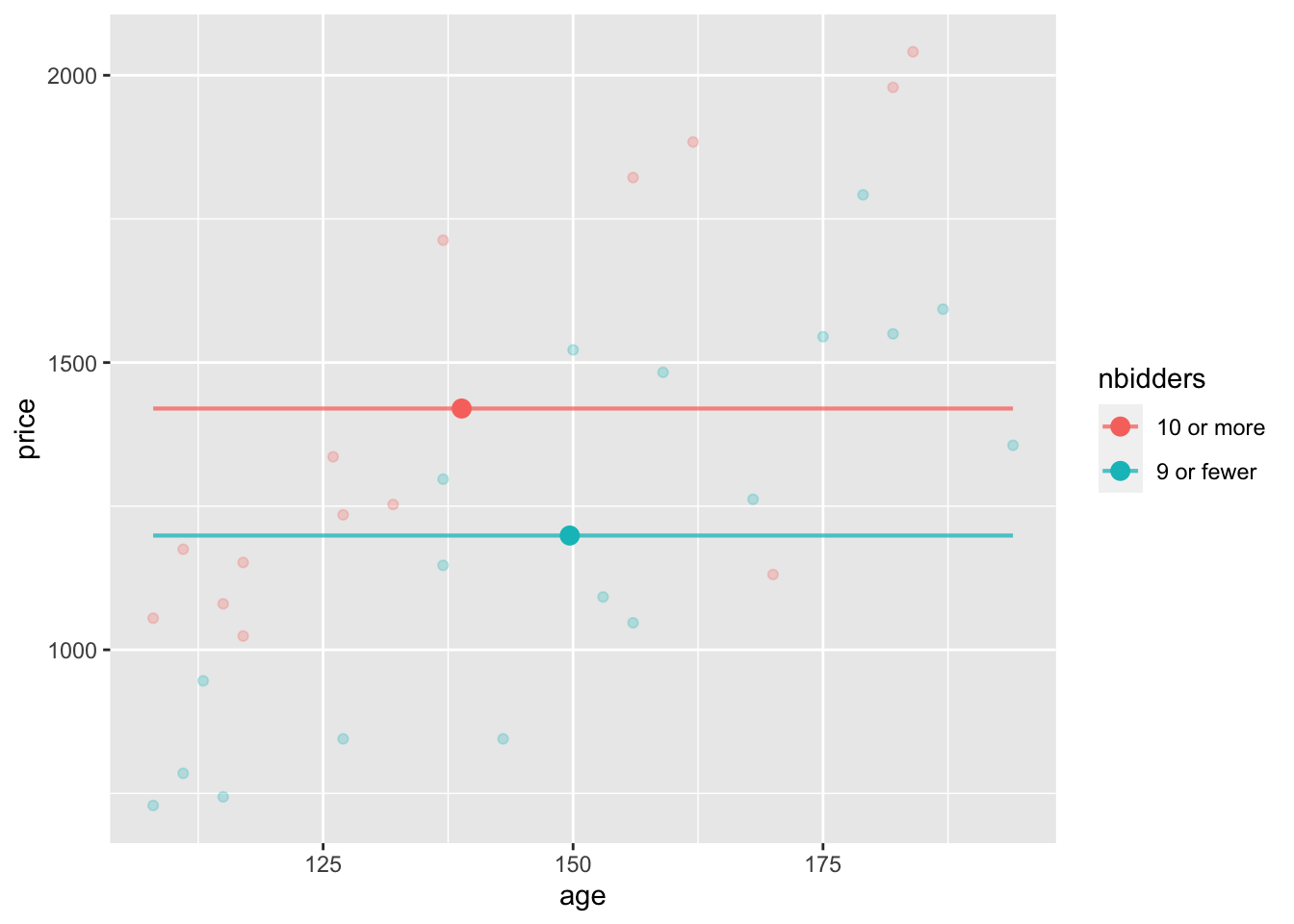

Part A. In the model without age as a covariate, what is the difference in mean prices for the 10-or-more-bidders group versus the 9-or-fewer-bidders group?

Part B. Now the picture when including age as a covariate. Adjusting for age, what is the difference in mean prices for the 10-or-more-bidders group versus the 9-or-fewer-bidders group?

mod2 <- lm(price ~ nbidders + age, data=Clock_auction) 

model_plot(mod2, x=age, color=nbidders) |>
  gf_point(mp ~ mage, color=~nbidders, data=Stats, size=3)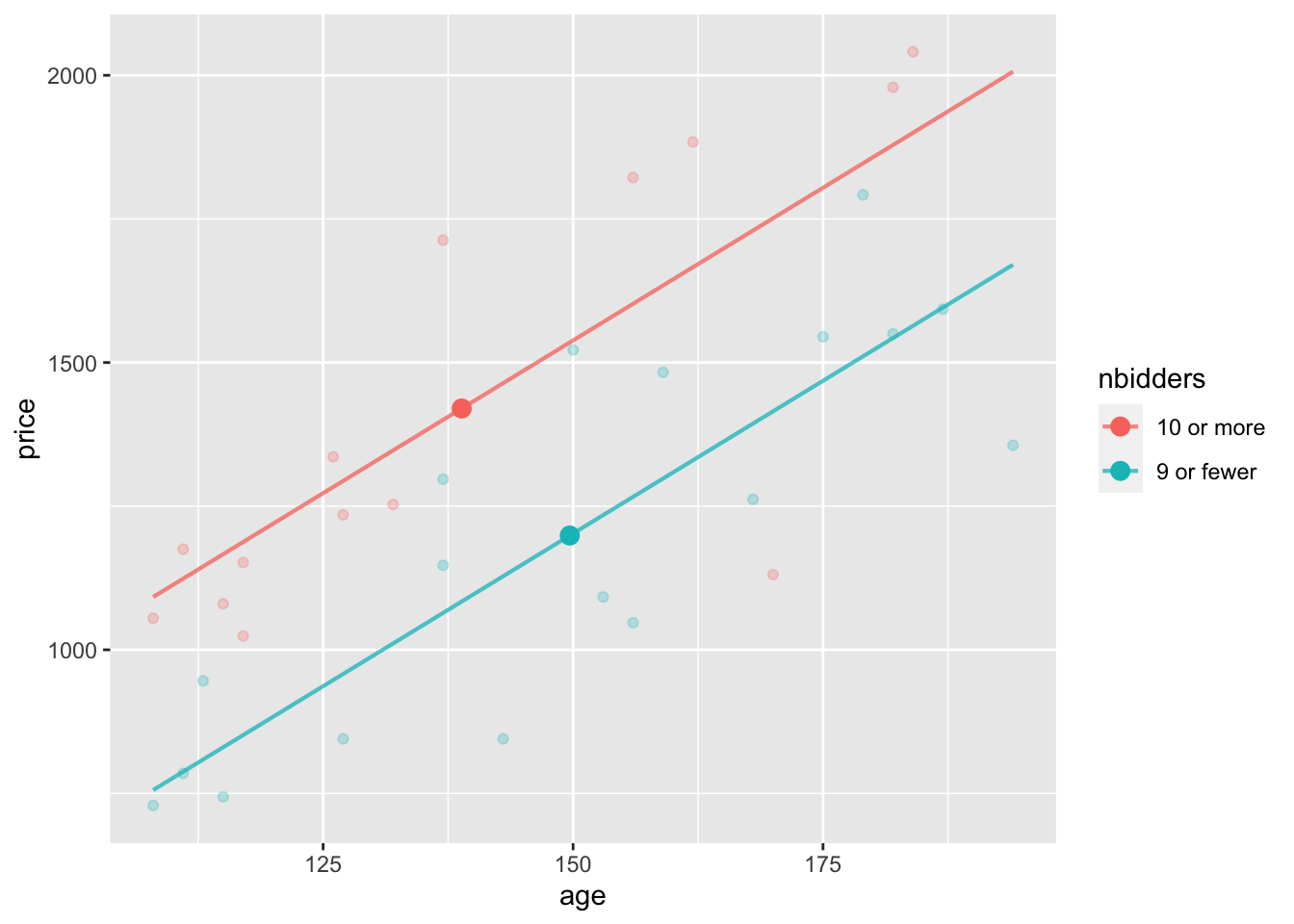

Part C. Here are confidence intervals for the two models graphed above. Explain what about these coefficients matches the conclusions you got in Parts (A) and (B)?

mod1 |> conf_interval()
# A tibble: 2 × 4
  term                .lwr .coef   .upr
  <chr>              <dbl> <dbl>  <dbl>
1 (Intercept)        1226. 1420  1614. 
2 nbidders9 or fewer -479. -221.   37.1
mod2 |> conf_interval()
# A tibble: 3 × 4
  term                  .lwr  .coef   .upr
  <chr>                <dbl>  <dbl>  <dbl>
1 (Intercept)        -467.    -56.3  354. 
2 nbidders9 or fewer -490.   -336.  -182. 
3 age                   7.79   10.6   13.5

This activity was inspired by schematic diagrams in Milo Schield’s Statistical Literacy: Seeing the story behind the statistics, 2011, pp. 224-5.