Exercises for Tutorial 1

At any point, you can submit your answers by collecting them and uploading them to the class site.

No answers yet collected

Link to upload site

If the answers that have been loaded automatically are not yours, press this button before starting your work:

Activity 1.1 Use Active R chunk 1.1 to look at the documentation for the penquins data frame. Then answer these questions in the essay box. (Note that the documentation uses the words “tibble” and “factor”, which are synonyms for “data frame” and “categorical variable” respectively.)

  1. In which archipelago were the data recorded?

  2. Which of the variables are categorical?

  3. What are the levels of the island variable?

  4. In what units is body mass recorded?

Active R chunk 1.1

Activity 1.2 The US Social Security administration publishes a data frame listing how many babies were given each name each year, starting in 1880. Here is a brief excerpt:

year sex name n prop
1880 F Abigail 12 0.00012294
1881 F Abigail 8 0.00008093
1882 F Abigail 14 0.00012101
1880 M Andy 58 0.00048986
1881 M Andy 58 0.00053564
1882 M Andy 51 0.00041793
1880 F Betty 117 0.00119871
1881 F Betty 112 0.00113297
1882 F Betty 123 0.00106314

Based on what you can see in the excerpt, what is the unit of observation in the data frame? Explain briefly the thinking behind your answer.

Activity 1.3 The Births78 data frame lists the number of babies born (births) each day of 1978 (date). Run the code in Active R chunk 1.2 to see the seasonal pattern.

Active R chunk 1.2
  1. In which season is the typical number of daily births the largest?
birth-season
late fall       late-winter       late-spring       late-summer      

  1. There is a funny pattern in the graph of births vs. date. There seem to be two parallel bands: a high band and a low band. Speculate on how this might have come about.
  2. Add another explanatory variable to the plot: wday. Does this help to explain the pattern from (2)? Say why or why not?
  1. There are a few points in the lower band that aren’t there for the usual reason. Hypothesize what’s going on with these outliers.

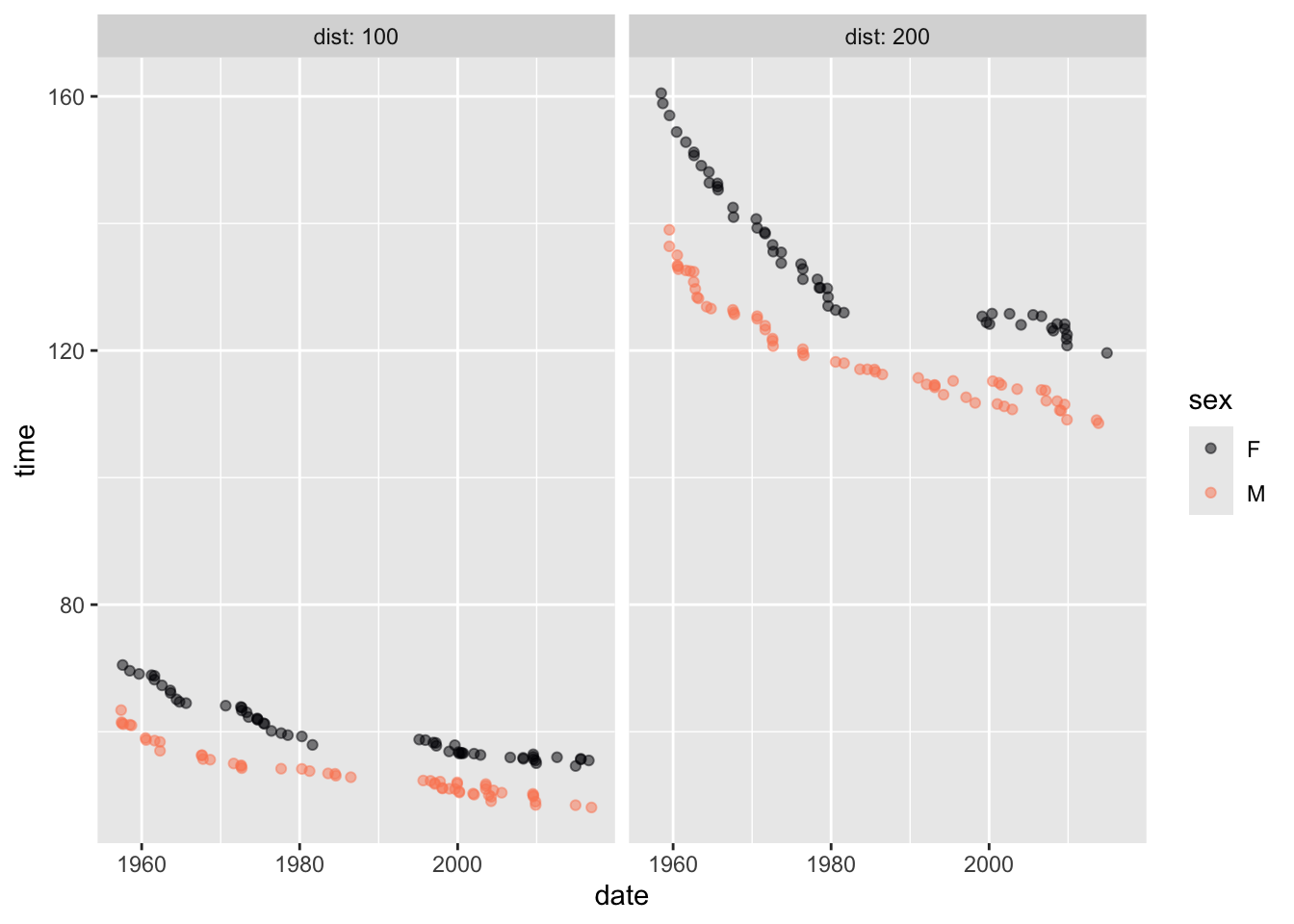
Activity 1.4 Using Active R chunk 1.3, recreate this graphic based on the Butterfly data frame. Butterfly contains records in the 100m and 200m swimming race.

Active R chunk 1.3

Activity 1.5 Penguins is a data frame covering 344 penguins near Palmer Station, Antarctica. One of the variables is mass, measured in grams. Use Active R chunk 1.4 to do the computations needed to answer the following questions. You’ll have to replace __wrangling_verb__ with the correct wrangling operation, and replace min() with the function appropriate for each question.

  1. What is the maximum body mass across all of the penguins? (Hint: the opposite of min().)
penguins-2-a
2710       4207       6300       8105      

  1. What is the mean body mass for all penguins?
penguins-2-b
2710       4207       6300       8105      

  1. Find the variance of the body mass variable. Explain why the number is so much bigger than the answers to (1) and (2). Also, say what are the units of the variance of mass.
Active R chunk 1.4

Activity 1.6 Each of the following graphics commands has a mistake. Fix them so that they all work:

Activity 1.7 Using Active R chunk 1.5, answer the following questions.

Active R chunk 1.5
  1. Which island has the largest penguins?
penguins-var-1
Biscoe       Dream       Torgersen      

  1. Perhaps you’re wondering, what about the conditions on the islands determines whether the penguins are large or small? It is a good idea, first, to see what other variables have to say about the matter. Color the points using species and facet with sex. In this new plot, does it seem that one of the islands is particularly favorable for high penguin mass?

Activity 1.8 Active R chunk 1.6 is initialized with wrangling code to count the number of penguins of each species and sex.

Active R chunk 1.6

Modify Active R chunk 1.6 to answer each of these questions in turn.

  1. Which island has 80 female penguins?
simple-wrangling-1
Torgersen       Biscoe       Dream      

  1. Which species inhabits all three islands?
simple-wrangling-2
Adelie       Gentoo       Chinstrap      

  1. In which year were there 57 male penguins?
simple-wrangling-3
2007       2008       2009       No such year      

In-class demonstration

Activity 1.9 When using point_plot(), the order of specimens in the data frame doesn’t matter. Each specimen is assumed to be independent of every other one. But many situations involve connections between the specimens. One subtle situation arises in clinical trials or other situations where the survival of specimens over time is of interest. You have likely heard of cancer studies of drugs where summary statistics like “median survival times” are compared between a control group and a group given the drug.

To illustrate the way that wangling can use a small set of action types to create specialized calculations, let’s look at survival in a study, named PREDIMED, of diet and risk of coronary heart disease. In this study, about two-thirds of the subjects were assigned to follow a “Mediterranean” diet; the other third, called the “Control” group, were not instructed to follow any particular diet. (In addition, the Mediterranean dieters were all given one of two supplements: extra-virgin olive oil (EVOO) or nuts.)

The Predimed data frame1 has the subject characteristics and results for the 6324 subjects whose outcome—serious cardiac event or not—could be determined at the end of the 7-year study. First, to orient ourselves, let’s look at the documentation:

Records from a 2003-2009 study of about 7000 people looking at the possible link between the Mediterranean diet and risk of coronary heart disease. The study name was PREDIMED (Prevención con Dieta Mediterránea)   Format: Data frame with 6324 rows and 15 variables - group assigned experimental group: control, MedDiet + extra virgin olive oil, MedDiet + nuts - sex - age - smoke former, current, or never smoker - bmi body mass index - waist waist circumference (cm) - wth waist to height ratio (cm/cm) - htn does the subject have hypertension - diab does the subject have type 2 diabetes - hyperchol does the subject have high LDL cholesterol - famhist family history of coronary heart disease in a first-degree relative before age 55 (for male relatives) or 65 (for women) - hormo for females, is the subject on hormone replacement therapy - p14 score on a 14-item dietary questionnaire to assess adherence to the Mediterranean diet. Scores lower than 10 indicate poor adherence to the Mediterranean diet. - toevent follow up time for the subject (years) - event did the subject have a “major cardiac event” in the follow-up period (median: 4.8 yrs)   Published report

Except for toevent and event, all measurements were made when the subject first enrolled in the study.

Active R chunk 1.7 prints a few rows and columns from Predimed

Active R chunk 1.7 
Predimed |>
  select(age, sex, group, event, toevent) |>
  head()
# A tibble: 6 × 5
    age sex    group          event toevent
  <dbl> <chr>  <chr>          <chr>   <dbl>
1    58 Male   Control        Yes      5.37
2    77 Male   Control        No       6.10
3    72 Female MedDiet + VOO  No       5.95
4    71 Male   MedDiet + Nuts Yes      2.91
5    79 Female MedDiet + VOO  No       4.76
6    63 Male   Control        Yes      3.15

Of the six people displayed, three had significant cardiac events. The event for the 71 year-old male happened 2.9 years after he enrolled in the study. In contrast, the 79 year-old female did not have a cardiac event. Or, more precisely, she had not had an event by the end of follow-up, 4.76 years after she entered the study. We don’t know what happened to her subsequently.

The PREDIMED study examined the “survival” of the subjects over time. At the start, 100% of the study participants had survived. At whatever time (toevent) that a subject had an event, the survival proportion goes down. For instance, restricting things for simplicity to the 6 people shown in Active R chunk 1.7, the survival was 100% up to 2.9 years. At that point, the surviving fraction was 5/6 (that is, 83.3%). The next event occurred at time 3.25 years. At this time, the survival went from 83.3% to 63.3%.

A mathematical nicety: If two of the six people at time 3.25 years have had events, shouldn’t the survival be 4/6 or 66.7%? Statisticians calculate the survival differently, recognizing that just before the event a time 3.25 years there were only 5 participants in the study, so the one event involves 20% of the surviving population.

In reality, people fall away from the study for reasons that are not cardiac events. For instance, a subject might move without providing a forwarding address.

Active R chunk 1.8 wrangles Predimed to produce a new column, prop_surviving.

Active R chunk 1.8

There are five wrangling statements in Active R chunk 1.8: select(), arrange(), and three mutate()s.

The select() merely discards variables that will not be needed for the calculation. This is purely for convenience, in case we want to debug the overall calculation.

  1. What is the arrange() doing?

The first mutate() command calculates the number still surviving up to the current event.

  1. What is the second mutate() doing?

The third mutate() uses a function cumsum() which gives the cumulative (or “running”) sum. For example, the cumulative sum of the series 2, 3, 1 is 2, 5, 6. After that, a specialized plot is made. (You are not expected to master gf_line(), other than to observe that it connects points with lines. You can switch to point_plot() if you like. Connecting with lines emphases the drops in survival.)

  1. What two functions in the overall calculation indicate that the order of the rows of the data frame being plotted is important?

  2. Toward the end of the time covered, the downward steps in survival become larger. Why?

The overall survival of the study participants is important, but for the purposes of the study, it’s important to look at things separately for the three different groups. Here, we are also interested in whether the sexes have different responses to the diet. Active R chunk 1.9 does the wrangling and makes an appropriate plot.

Active R chunk 1.9
  1. Using the graphic from Active R chunk 1.9, summarize the results from the study.

No answers yet collected

Submit collected answers here

Footnotes

  1. The datafile is from James Scott, SDS323: Statistical Learning and Inference link↩︎