A Model Statistics Course

presentation
overview
Author

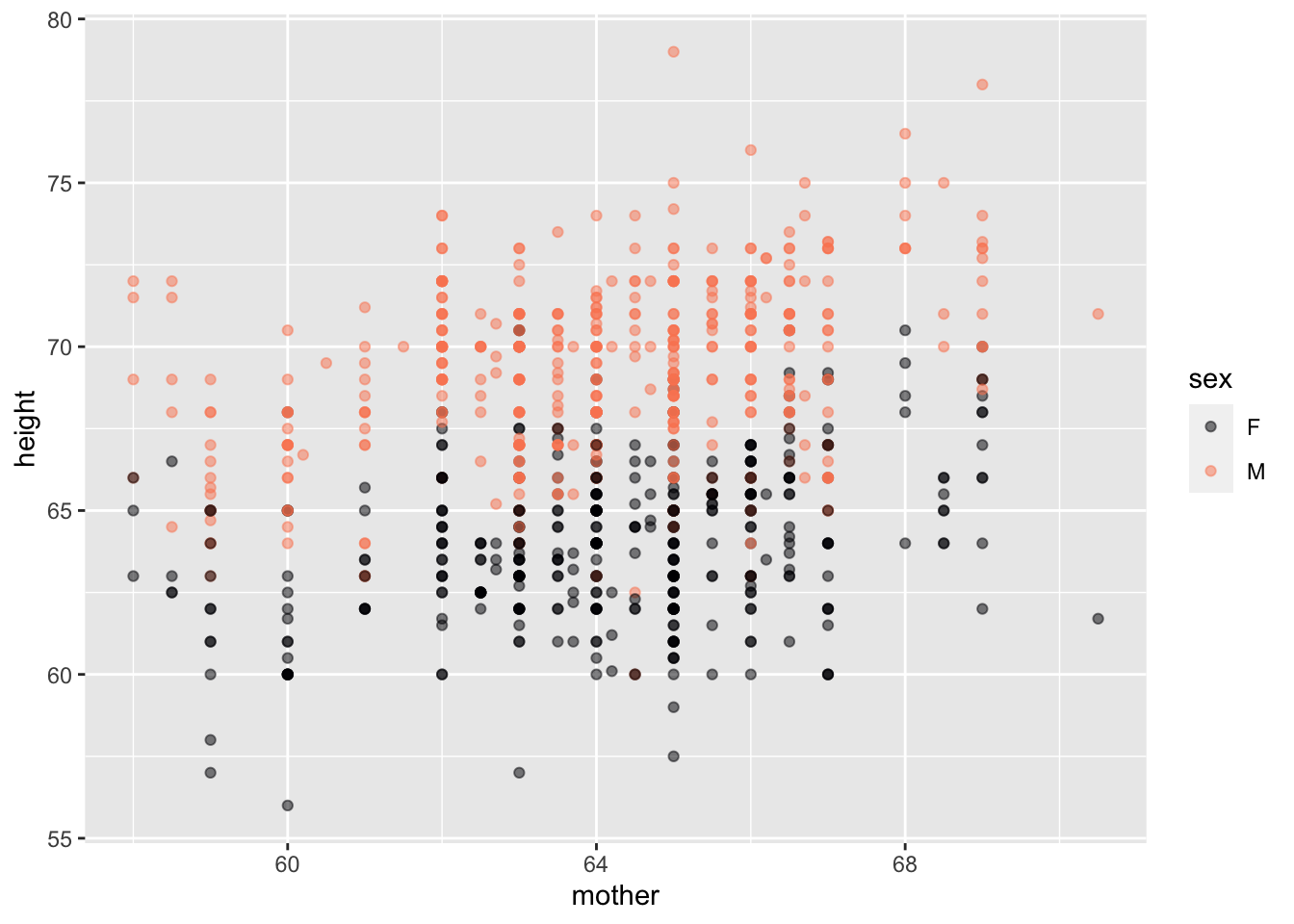
Daniel Kaplan

Published

January 31, 2024

These are presentation notes for the October 2023 StatChat meeting. For more than 15 years, statistical educators in the Twin Cities region of Minnesota have been gathering a half-dozen times a year at StatChat to share comradeship and teaching insights. Among the schools regularly represented are the University of Minnesota, Macalester College, St. Olaf College, Hamline University, Augsburg University, Carleton College, St. Cloud State University, and Minnesota State University Mankato. The slides were slightly revised for a 2024-01-31 presentation “StatsChat” for high-school teachers in Wisconsin.

Abstract: “Mere Renovation is Too Little Too Late: We Need to Rethink Our Undergraduate Curriculum from the Ground Up” is the title 2015 paper by George Cobb. Honoring George’s challenge, I have been rethinking and re-designing the introductory statistics course, replacing traditional foundations using modern materials and reconfiguring the living and working spaces to suit today’s applied statistical needs and projects. In the spirit of a “model house” used to demonstrate housing innovations, I’ll take you on a tour of my “model course,” whose materials are available free, open, and online. Among the features you’ll see: an accessible handling of causal reasoning, a unification of the course structure around modeling, a highly streamlined yet professional-quality computational platform, and an honest presentation of Hypothesis Testing that puts it in the framework of Bayesian reasoning.

Introductions

  1. What is the most important take-away from your stats course?

  2. What subjects could be dropped without loss?

  3. Are there course topics that are misleading?

  4. Are there course topics that are out of date?

Motivation

The “consensus” Stat 101 is 50 years out of date:

  1. fails to engage issues of causation, covariation, and adjustment
  2. too much emphasis on p-values
  3. entirely ignores Bayes
  4. no substantial coverage of risk, risk factors, …
  5. uses a confusing over-variety of graphic modes (many of which are out-of-date)
  6. doesn’t make contact with data science, machine learning, and AI/GPT

I’m happy to discuss the above points anytime, but that’s where I aimed this talk.

My objectives:

  1. Demonstrate the extent to which it’s possible to overcome these deficiencies with a complete, practicable, no-prerequisite course.

  2. Provide a complete course framework, avoiding topic bloat, to which other people can add their own exercises, topics, and examples.

To this end, there is now a completed draft textbook: Lessons in Statistical Thinking that is free, online.

Jeff Witmer’s approach

Jeff proposes 15 changes*, dividing them into amount-of-effort categories:

  1. Changes You Could Make with Little Effort or Planning. (e.g. “significant” -> discernible)
  2. Changes to a Course That You Could Implement after Investing a Day or so of Planning. (e.g. emphasize power, not \(\alpha\))
  3. Changes to a Course That Would Require Quite a Bit of Planning but That Are Worth Considering Nonetheless (e.g. emphasize effect size)

Jeff Witmer (2023) “What Should We Do Differently in STAT 101?” Journal of Statistics and Data Science Education link

Almost all of which are engaged in Lessons in Statistical Thinking

Style

  1. Demonstrate and describe statistical phenomena by causal simulation
    • Examples:
      • sampling variation
      • confounders, covariates, colliders, adjustment
    • Stat theory from simulation/wrangling rather than probability/algebra
  2. Informal inference from the very beginning, gradually formalizing it over the semester
  3. Single, standard format for graphics: the annotated point plot.
    • Annotations for (i) distribution, and (ii) models, including multivariable models.
  4. Keep the software powerful, but simple.
    1. Example: a point plot of Francis Galton’s data on children’s heights versus their parents.
Galton |> point_plot(height ~ mother + sex)

  1. Example: The most frequently encountered command has this structure:
    Galton |> 
      model_train(height ~ mother + sex) |>
      conf_interval()
# A tibble: 3 × 4
  term          .lwr  .coef   .upr
  <chr>        <dbl>  <dbl>  <dbl>
1 (Intercept) 37.1   41.4   45.8  
2 mother       0.286  0.353  0.421
3 sexM         4.87   5.18   5.49

Course overview

  • Part 1: Handling data
    • Data frames
    • Graphics (data and models)
    • Wrangling
  • Part 2: Describing relationships
    • Regression (incl. categorical and multiple explanatory variables)
    • Adjustment
  • Part 3: Randomness and the unexplained
    • Signal and noise
    • Simulation and DAGs
    • Probability models (optional)
    • Sampling variation and confidence intervals/bands
    • Likelihood (optional, prep. for Part 5)
    • Measuring and accumulating risk
  • Part 4: Causal reasoning
    • Effect size
    • Directed Acyclic Graphs (DAGs), or “influence diagrams”
    • Causality/Confounding/Adjustment
    • Experiment
  • Part 5: Hypothetical thinking
    • Basic Bayes: competing two hypotheses
    • Hypothesis testing

How can we fit more in an already crowded course?

Streamline!

  1. Reduce drag cognitive load.
    1. Repeated use a small number of standard forms
      • one basic graphical pattern: annotated point plot
      • one basic computational pattern: noun |> verb |> verb |> …
    2. Avoid nomenclature conflicts with everyday words, e.g.
      • “table” -> data frame
      • “case” -> specimen
      • “assignment” -> storage
  2. Unify t, p into regression modeling, conf. interval/bands in both graphics and models
  3. Keep number of types of objects small: data frame, model, graphic, simulation
    1. Very small computational footprint, a dozen stat/graphics/wrangling functions.
  4. Remove square roots whenever that’s easy
    • focus on variance rather than standard deviation, R^2 rather than r

Part I: Handling Data (6-7 class hrs)

Lesson 1. Data frames

Data is always in data frames.

  • Columns: Variables

  • Rows: “Specimens” / Unit of observation

Computing concepts:

  • name of data frame, e.g. Galton or Nats
  • pipe
  • function()

Usually start with a named data frame, piping it to a function.

Nats |> names()
[1] "country" "year"    "GDP"     "pop"

Lesson 2. Graphics

Both the horizontal and vertical axes are mapped to variables.

Just one command: point_plot() produces point plot with automatic jittering as needed.

Tilde expression specifies which variable is mapped to y and x (and, optionally, color and faceting).

Galton |> point_plot(height ~ sex)
Galton |> point_plot(height ~ mother + father + sex)

Lesson 3. Empirical distributions

Galton |> point_plot(height ~ sex, annot = "violin")

Lesson 4. Models as graphical annotation

Galton |> sample_n(size=100) |> 
  point_plot(height ~ sex, annot = "model", 
             point_ink = 0.1, model_ink=0.75)

Galton |> point_plot(height ~ mother + father + sex, 
                     annot = "model", 
                     point_ink = 0.1, model_ink=0.75)

Lesson 5: Wrangling

[Perhaps use two class days]

Five basic operations: mutate(), filter(), summarize(), select(), arrange()

Nats
# A tibble: 8 × 4
  country  year   GDP   pop
  <chr>   <dbl> <dbl> <dbl>
1 Korea    2020   874    32
2 Cuba     2020    80     7
3 France   2020  1203    55
4 India    2020  1100  1300
5 Korea    1950   100    32
6 Cuba     1950    60     8
7 France   1950   250    40
8 India    1950   300   700
Nats |> filter(year == 2020)
# A tibble: 4 × 4
  country  year   GDP   pop
  <chr>   <dbl> <dbl> <dbl>
1 Korea    2020   874    32
2 Cuba     2020    80     7
3 France   2020  1203    55
4 India    2020  1100  1300
Nats |> summarize(totalpop = sum(pop), .by=year)
# A tibble: 2 × 2
   year totalpop
  <dbl>    <dbl>
1  2020     1394
2  1950      780

Lesson 6: Computing recap

[Perhaps merged into a two-day wrangling unit with Lesson 5]

Pipes, functions, parentheses, arguments, …

Lesson 7: Databases

[Entirely optional]

  • Joins
  • Why we put related data into separate tables with different units of observation.

Part II: Describing Relationships

Consistently use explanatory/response modeling paradigm. Introduce models with two or three explanatory variables early in the course.

Use variance as measure of variation of a variable. (Ask me about the simple explanation of variance that doesn’t involve calculating a mean.)

Use data wrangling to introduce model values, residuals, …

mtcars |> 
  mutate(mpg_mod = model_values(mpg ~ hp + wt)) |> 
  select(hp, wt, mpg_mod) |> 
  head()
                   hp    wt  mpg_mod
Mazda RX4         110 2.620 23.57233
Mazda RX4 Wag     110 2.875 22.58348
Datsun 710         93 2.320 25.27582
Hornet 4 Drive    110 3.215 21.26502
Hornet Sportabout 175 3.440 18.32727
Valiant           105 3.460 20.47382

Then transition to model coefficients.

mtcars |>
  model_train(mpg ~ hp + wt) |>
  conf_interval()
# A tibble: 3 × 4
  term           .lwr   .coef    .upr
  <chr>         <dbl>   <dbl>   <dbl>
1 (Intercept) 34.0    37.2    40.5   
2 hp          -0.0502 -0.0318 -0.0133
3 wt          -5.17   -3.88   -2.58

Coefficients are always shown in the context of a confidence interval, even if they don’t yet know the mechanism for generating such intervals.

Demonstrate mechanism of “adjustment”: Evaluate model holding covariates constant.

Part III: Randomness and noise

6-11 class hours, depending on how much spent with named probability distributions. (USAFA engineers want some practice with named distributions: normal, exponential, poisson, …)

Signal and noise

Simulations

Students construct simple simulations, using them to generate data.

mysim <- datasim_make(
  x <- rnorm(n),
  y <- 2 + 3*x + rnorm(n, sd=0.5)
)
mysim |> sample(size=4)
# A tibble: 5 × 2
       x       y
   <dbl>   <dbl>
1  0.552  3.97  
2 -0.675 -0.0812
3  0.214  3.10  
4  0.311  2.82  
5  1.17   5.79

Probability models

Mostly using simulations.

Likelihood

Early introduction of the concept of likelihood: probability of data given hypothesis/model.

  • main point: distinguish between p(model | data) and p(data | model)
  • we’ll use likelihood in last part of course.

R2

Prediction

  1. The proper form for a prediction: a relative probability assigned to each possible outcome.

  2. The prediction-interval shorthand for (a).

Sampling variation and confidence intervals

Runs <- mysim |> 
  sample(n = 5) |>
  model_train(y ~ x) |> 
  trials(10) 
Warning: The `tidy()` method for objects of class `model_object` is not maintained by the broom team, and is only supported through the `lm` tidier method. Please be cautious in interpreting and reporting broom output.

This warning is displayed once per session.
Runs |> select(.trial, term, estimate )
   .trial        term estimate
1       1 (Intercept)    1.659
2       1           x    3.164
3       2 (Intercept)    2.204
4       2           x    2.950
5       3 (Intercept)    2.055
6       3           x    3.318
7       4 (Intercept)    1.771
8       4           x    3.141
9       5 (Intercept)    2.156
10      5           x    2.920
11      6 (Intercept)    2.157
12      6           x    3.324
13      7 (Intercept)    2.091
14      7           x    2.833
15      8 (Intercept)    2.446
16      8           x    2.794
17      9 (Intercept)    1.892
18      9           x    2.399
19     10 (Intercept)    2.053
20     10           x    2.694
Runs |> summarize(var(estimate), .by = term)
         term var(estimate)
1 (Intercept)       0.05117
2           x       0.08504

Demonstrate that variance scales as 1/n. 

Risk

(2 or 3 day unit)

Definition of risk, risk factors, baseline risk, risk ratios, absolute change in risk.

Use absolute change for decision making, but use risk ratios and odds ratios for calculations.

Regression when response is a zero-one variable.

Whickham |> point_plot(outcome ~ smoker, annot="model", 
                       model_ink = 1)

Whickham |> point_plot(outcome ~ age + smoker, annot="model")

Part IV: Causal modeling

Effect size

Ratio of (change in output) to (change in input).

Physical units important.

DAGs

Reading “influence diagrams”

Causality

confounding, covariates, and adjustment

Choosing covariates based on a DAG

Experiment

experiment interpreted as re-wiring of DAGs: requires intervention

Part V: Hypothetical thinking

Strong emphasis on the idea of hypothesis.

  • Your turn: Please define hypothesis.

What we want: p(hypothesis | data)

What we have: hypothesis |> simulation |> data summarized as a Likelihood.

Question: How do we calculate what we want.

Bayes framework

  • Setting: medical screening. Test result + or -.

  • We put two hypotheses into competition based on the test result.

  • Likelihoods we can measure from data:

    • p(+ | Sick) aka “sensitivity”
    • p(+ | Healthy) aka “false-positive rate” translated to “specificity”

  • Setting: prevalence(Sick)

  • Calculation

    • Graphically
    • Algebra from the graph
    • Formula in Likelihood-ratio form

\[odds(Sick|+) = \frac{p(+ | Sick)}{p(+ | Healthy)} \ odds(prevalence)\]

Null hypothesis testing

Null is “Healthy.”

We have no claim about \(prevalence\).

If we have no claim about \(p(+ | Sick)\), we are more inclined to conclude \(Sick\) if \(p(+ | Healthy)\) is small.

  • \(p(+ | Healthy)\) is p-value.

Neyman-Pearson

Null is “Healthy.” Alternative is “Sick”.

We have no claim about \(prevalence\), but we have the ability to estimate \(p(+ | Sick)\).

Inclined to conclude \(Sick\) if \(p(+ | Healthy)\) is small (like HNT) and \(p(+ | Sick)\) is small. \(p(+ | Sick)\) is the power of the test.

Gotcha’s in HT

  • Without power, can’t say what constitutes a big p-value.
  • Estimation of p suffers greatly from sampling variation. No good reason to think that p < 0.01 is any different from p < 0.05.
  • Sensible decisions require knowledge of prevalence.
  • Effect size, not p-value, is needed to interpret practical importance of results.

Objects and operations

  1. Data frame
  2. Data graphics (as distinct from “infographics”)
  3. Statistical model
  4. Simulation

Operations for all students

  1. Data wrangling (simplified)
  2. Annotated point plot of variables from a data frame
  3. Model training
  4. Model summarization

Operations used in demonstrations (and suited to some students)

  1. Simulation (in demonstrations)
  2. Iteration and accumulation (in demonstrations)

Computations on variables are always inside the arguments of a function taking a data frame as an input.

Tilde expressions for models and graphics.

Resources

  1. Textbook: Statistical Inference via Data Science by Chester Ismay and Albert Y. Kim
  2. Textbook: Lessons in Statistical Thinking by Danny Kaplan
  3. USAFA Math 300Z course outline, instructor notes, etc.
  4. Jeff Witmer (2023) “What Should We Do Differently in STAT 101?” Journal of Statistics and Data Science Education link